联合订货下基于φ-散度的多产品库存鲁棒优化模型

孙 月，邱若臻

(东北大学 工商管理学院，辽宁 沈阳 110169)

0 引言

在激烈变化的市场竞争环境下，库存管理作为一个必要手段，为企业创造了可持续竞争优势，合理的库存管理策略能够在保持较高客户服务水平的同时，有效控制企业库存水平，创造更多利润。长期以来，基于报童模型的库存控制问题一直是供应链管理领域的研究热点[1]。传统研究大多考虑单一产品并假设市场需求或产出等不确定因素服从已知随机分布，通过优化期望利润或成本获得最优库存策略。在Arrow等[2]对单周期库存问题进行了开创性的研究之后，多产品库存问题进一步得到了广泛研究。

Wang等[3]假设市场需求不确定，建立了单周期多产品库存模型，并从理论上分析了模型的最优性条件。Serel[4]对带有预算约束的多产品报童问题加以拓展，考虑二次订货问题，有效利用更新市场需求信息的快速反应机制，为整个销售季节确定订货量。Shi和Zhang[5]在需求不确定环境下研究了考虑供应商折扣的多产品联合采购、定价问题。Kouki等[6]研究了具有随机寿命的N种易腐产品联合订货问题，在产品需求服从泊松分布假设下给出了连续检查(s,c,S)库存策略。潘林和周水银[7]在确定性需求下，采用博弈论方法研究了不同捆绑策略下的多产品供应链定价问题。上述研究要么假设需求是确定性的，要么假设已知随机需求的概率分布信息。然而，在企业实际经营过程中，面对的不确定因素日益增加，企业自身在掌握这种不确定性方面通常缺乏充分的专业知识，导致完备需求信息的假设难以适用实际要求。正如Beyer和Sendhoff[8]指出，对未知参数的任何不当假设，都将可能造成严重的绩效损失。这就迫使决策者寻求一种能有效应对日益增加的不确定性扰动的决策方法。

鲁棒优化，作为处理不确定性问题的有效手段,近年来受到广泛关注[9]。应用鲁棒优化方法研究未知需求分布的库存控制问题可追溯到1958年，Scarf等[10]给出了仅知需求均值和方差的报童订货策略。此后，许多学者将这一方法应用于仅知部分需求信息的库存控制问题中。例如，Vairaktarakis[11]利用区间和离散需求情景描述需求不确定性，研究了带有预算约束的鲁棒多产品报童问题。Lin和Ng[12]针对仅知需求区间信息的多市场单产品报童问题，给出鲁棒订货策略。Kwon和Cheong[13]考虑了仅知需求均值和方差的单周期单产品库存控制模型，给出最优库存策略。Carrizosa等[14]采用鲁棒优化方法研究了带有自回归需求的单产品报童问题。Hanasusanto等[15]针对风险规避多产品报童模型，利用二次决策规则将所建鲁棒优化模型转化成易于求解的半定规划问题，并给出了有效的数值解。Park和Lee[16]采用分布式鲁棒优化方法求解带有多个不可靠供应商和随机需求的单周期单产品库存问题。由上述研究可以看出，目前鲁棒优化方法在解决不确定环境下的库存控制问题时主要采用区间或相应矩信息对不确定性进行建模。然而，采用这种事先指定的不确定集可能会丢失相关数据的重要信息，从而对最终决策带来不利影响[17]。此外，相关参数信息的精确指定需要决策者具备专业的知识，使得这一方法具有一定的局限性。

近年来，随着数据科学的发展，数据可得性问题备受关注，由此催生出了基于数据驱动的供应链运作管理问题研究。在库存控制领域，Bertsimas和Thiele[18]针对经典报童问题，采用基于非参数估计的数据驱动方法给出了考虑风险厌恶的报童订货策略。针对同样的问题，Uichanco[19]假设仅知来自未知需求分布的样本数据，采用样本平均近似方法研究了报童订货问题。Huh等[20]针对随机库存控制问题，采用梅耶(Kaplan-Meier)估计方法给出了相应的库存策略。在同样的假设条件下，Klabjan等[21]针对单一产品多周期周期性检查随机订货批量问题，提出了一种融合数据拟合和库存优化的最小最大鲁棒模型。同样地，Ben-Tal等[22]针对离散情景概率不确定情况，给出了仅知历史需求数据的报童策略。Sachs和Minner[23]在自由分布框架下，采用数据驱动方法研究了考虑销售损失的报童问题，并将这一方法下库存绩效与其他参数和非参数估计方法进行比较，发现数据驱动报童模型能够很好地处理高度审查和价格依赖的需求。邱若臻等[24]利用φ-散度构建了不确定需求概率分布的置信域，并针对风险厌恶的管理者建立了基于条件风险值的单产品单周期库存鲁棒优化模型。Mamani等[25]针对不确定需求构建了基于中心极限定理的不确定集，给出了封闭形式的鲁棒订货决策。

由上述研究可以看出，多产品库存控制问题研究主要侧重于以下几方面：(1)多数研究集中于已知完备需求随机分布信息，通过优化期望成本或利润获得最优库存策略；(2)采用鲁棒优化方法处理库存系统中的不确定性时大多针对单一产品库存系统，并且假设事先已知不确定参数的不确定集；(3)部分学者虽然采用数据驱动方法探讨了库存控制问题，但未考虑是否存在具有某种结构的最优库存管理策略，并且通常仅针对单一产品库存系统。此外，对多产品联合订货导致的固定订货成本鲜有涉及。基于此，本文在上述研究基础上，进一步考虑固定订货成本的多产品联合库存控制问题，在仅知每种产品市场需求历史数据基础上，采用基于φ-散度的数据驱动方法构建满足一定置信度要求的未知需求概率分布的不确定集，建立了基于最小最大准则的多产品库存鲁棒优化模型。在此基础上，证明了(s,S)库存策略的最优性并给出了相关策略参数的求解方法。最后，通过数值算例验证了所建模型及求解方法的有效性。

1 考虑联合订货成本的多产品库存基本模型

考虑单周期环境下面临不确定市场需求的零售商多产品库存管理问题。为满足不同客户对不同产品的需求，零售商共经营J(J为一正整数)种产品。在销售季节来临之前，零售商需要确定每种产品j(j=1,2,…,J)是否需要订货及订购多少数量。如果产品j需要订货，则支付单位采购成本cj。假设零售商采取联合订货的方式，每次联合订货导致的固定成本为K0。销售期开始，零售商以单位价格rj出售产品j；在销售期末，如产品j有剩余，则导致单位产品库存持有成本hj；而对于未满足需求的部分，将导致单位缺货成本lj。

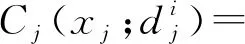
(1)

其中，式(1)中进一步考虑了零售商销售收入，因此，文中最小化库存总成本可等价转化为最大化利润问题。当考虑联合订货固定成本时，零售商多产品库存优化问题可表述为

cj(xj-x0j)+Cj(xj)Tpj}

(2)

2 不确定需求概率下的多产品库存鲁棒优化模型及最优库存策略

当每种产品的市场需求分布未知时，不失一般性，令Uj表示产品j的市场需求概率分布所隶属的不确定集，即pj∈Uj，j=1,2,…,J，则在最大最小准则下，式(2)鲁棒对应可描述为

(3)

针对单一产品库存控制问题，已有研究证明了当不确定市场需求随机分布已知时，存在形如(s,S)形式的最优库存策略使得库存成本最低，其中，s是再订货点，S是订货至水平[10]。下面将针对未知需求分布下的多产品库存控制，通过分析式(3)的结构属性探讨是否仍存在某种策略结构使得库存成本最低。对于单一产品库存控制问题，为了证明(s,S)库存策略的最优性，文[10]定义了一维实数空间上的K-凸函数。在此基础上，文[26]进一步将其扩展到n维空间，定义K0-凸函数如下，即

定义1对于函数φ(u):n→:1，K0≥0,如果不等式

(4)

对∀v≥0,v∈n，λ<0，λ∈和∀u∈n均成立，则函数φ(u)是K0-凸函数。

进一步，文[27]指出，上述定义等价于，如果对任意的u1≤u2,λ∈[0,1],下式成立，即

φ(λu1+(1-λ)u2)

≤λφ(u1)+(1-λ)[φ(u2)+K0δ(eT(u2-u1))]

(5)

则函数φ(u):n→1是K0-凸函数,K0≥0。在几何上，函数φ(u)是K0-凸函数当且仅当所有中间点(λu1+(1-λ)u2,φ(λu1+(1-λ)u2)),λ∈[0,1]，位于点(u1,φ(λu1))和(u2,φ(λu2)+K0δ(eT(u2-u1))连接线段的下方。

为了方便描述，定义函数g(x)如下:

(5)

(7)

则在K0-凸函数定义基础上，有如下引理1成立，即

根据引理1，函数g(x)存在一个全局极小值点S=(S1,S2,…,SJ)T∈J，定义集合

Ξ={x≤s|g(x)=g(S)+K0}

(8)

显然，集合Ξ是非空有界的。令

(9)

σ={x≤S|x∉Σ}

(10)

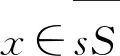
(i)如果x∈Σ，则g(x)≤K0+g(S)；

(ii)如果x∈σ，则g(x)>K0+g(S)。

上述引理2暗含当产品的库存水平属于集合Σ时，零售商不订货时产生的库存成本低于订货后产生的库存成本，因此，零售商的最优决策是选择不订货，以当前库存量进行销售；当产品的库存水平属于集合σ时，零售商将选择订货，订货数量为q=S-x>0。

引理3对于连续K0-凸函数g(x)，考虑联合订货成本的多产品库存鲁棒优化问题(3)等价于

(11)

其中，S=(S1,S2,…,SJ)T是函数g(x)的全局极小值点。并且，函数f(x0)连续且在{x0≤S}上是K0-凸函数。

根据引理3及其证明过程，得如下定理1，即

定理1对于联合订货下的多产品库存鲁棒优化问题(3)，存在最优(s,S)的库存策略。当初始库存水平x0∈σ时，将库存补充至S；当初始库存水平x0∈Σ时，则不订货。即，最优订货量为

(12)

其中，集合Σ和σ定义如式(9)和式(10)所示。

上述定理1给出了需求分布未知条件下，考虑联合订货的多产品最优(s,S)库存策略结构。然而，参数s和S的确定依赖于产品市场需求分布所隶属的不确定集。下面利用基于φ-散度的数据驱动方法，针对每一种产品j(j=1,2,…,J)，探讨如何在一定置信水平下构建未知需求概率分布的不确定集Uj，从而通过求解问题(3)确定最优库存策略参数。

3 基于φ-散度的数据驱动多产品库存鲁棒优化策略

3.1 未知需求概率分布的不确定集构建

传统供应链库存鲁棒优化问题的研究通常采用事先给定的具有某种结构属性的不确定集，以保证获得易于处理的鲁棒对应。然而，该方法通常难以保证真实的系统参数，如需求概率，落在事先给定的不确定集内。基于此，本文将针对产品的历史销售数据，利用φ-散度构建满足一定置信水平的不确定概率的置信域。对于向量p=(p1,p2,…,pm)T≥0和q=(q1,q2,…,qm)T≥0，φ-散度定义为

(13)

其中，φ(t)(t≥0)是凸的，称为φ-散度函数。不失一般性，假设函数φ(t)(t>0)连续且二次可微，φ(1)=0，φ″(1)≠0。对于a>0，0φ(a/0):=alimt→∞φ(t)/t，0φ(0/0):=0。当向量p和q是随机变量的概率向量时，式(13)定义了向量p和q之间的距离，且满足pTe=1，qTe=1。

由定义(13)可知，不同散度函数φ(·)的选择直接影响对向量p和q之间距离的度量。表1给出了常见的φ-散度及其共轭函数[23]。其中，φ*(·)表示函数φ(·)的共轭，φ*(·):→∪{∞},定义为显然，φ*(s)是凸函数。

表1 常见的φ-散度及其共轭函数

(14)

上式表明以不低于1-α的概率保证了产品j的真实概率pj落在式(14)所示的集合内。需要指出的是，上述φ-散度数据驱动方法仅适用于离散需求概率分布不确定集构建，可广泛应用于当决策者仅仅知道需求的历史数据，但无法获得真实的需求概率分布时，如何在已有数据基础上通过优化期望利润(成本)或其他绩效指标进行决策制定的情况。例如，对于销售某一季节性商品的零售商，当其无法获得精确的产品需求分布信息时，为了在销售季节来临前确定合适的订货量决策，可在其历史销售数据基础上采用φ-散度数据驱动方法构建产品需求概率分布不确定集，结合鲁棒优化建模思想构建利润最大化模型，并通过求解所建模型确定鲁棒订货量决策，以此应对需求不确定性扰动。

3.2 最优(s,S)库存策略参数的确定

为寻找每种产品的最优订货至库存水平S，考虑式(6)函数g(x)最小化问题，即

(15)

在如式(14)所示不确定集条件下，式(15)内部极大化问题可描述为

(16)

问题(16)的拉格朗日函数为

其中，φ*(·)是函数φ(·)的共轭，凸函数。因此，函数ψ(λj,ηj)是关于(λj,ηj)的凸函数。问题(16)的拉格朗日对偶问题为

(18)

考虑如下问题

s.t.λj≥0,j=1,2,…,J

(19)

下面进一步讨论如何确定再订货点s。给定Sj，sj是满足下述方程的最大的yj(yj≤Sj)，即

(20)

上式等号左边是产品j不订货时最坏情况下的库存期望成本，等号右边是当产品j初始库存水平为yj，补货至Sj时最坏情况下的库存期望成本。式(20)表明再订货点sj是驱动库存管理者是否进行补货并将当产品j的库存补充至Sj的临界点。再订货点sj可通过求解下述问题获得，即

(21)

定理3对于j=1,2,… ,J，考虑如下问题

λj≥0,j=1,2,…,J

(22)

4 数值分析

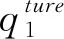
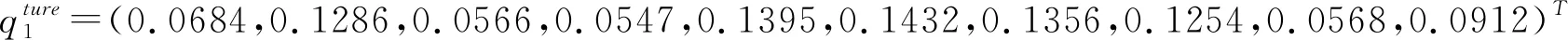
(3)选择常见的Kullback-LeiblerL(KL)散度和Cressie-Read(CR)散度，置信水平分别设为95%和99%，以步骤1、2的数据为基础，在需求概率分布未知时，分别求解问题(19)和(22)得到不同样本规模、φ-散度和置信水平1-α下的鲁棒库存策略及相应的多产品库存绩效。

表2 真实分布下的库存策略及绩效

基于KL散度和CR散度，在95%和99%置信水平下，得到的不同样本规模下的鲁棒库存策略如表3和表4所示。

表3 产品1在不同样本规模、φ-散度、置信水平下的鲁棒库存策略

表4 产品2在不同样本规模、φ-散度、置信水平下的鲁棒库存策略

由表3和表4可知样本容量越大，两种产品的鲁棒库存策略越接近最优情况。这是由于样本容量越大，基于样本估计的需求概率qNj,j=1,2，越接近真实情况，依此构建的不确定集越精确，因此，两种产品的订货策略越接近其在真实概率分布下的最优订货策略。为了检验鲁棒库存策略导致的绩效损失，进一步求得了在真实分布下应用鲁棒库存策略时得到的多产品库存绩效，结果如下图1和图2所示。

图1 CR散度下的多产品库存成本绩效

图2 KL散度下的多产品库存成本绩效

由图1和图2可以发现，无论是在CR散度还是KL散度下，基于不同的置信水平，最坏情况下的鲁棒多产品库存成本均随着样本规模的增加而降低。这是由于样本规模越大，库存管理者所能获得的决策信息越准确，因此，依据文中方法得到的库存成本下限越低。特别地，当在真实需求概率分布下应用鲁棒库存策略时，两种散度函数下得到的多产品库存绩效同样受样本容量大小的影响，但影响较小。此外，随着样本容量的增加，鲁棒库存策略在真实分布下的库存绩效越接近最优情况(-2368.9)。由图1和图2可以进一步看出，基于φ-散度的鲁棒库存策略导致的绩效损失随样本容量的增加而减小,表明决策者获得的历史需求数据样本量越大，依据文中数据驱动方法做出的决策越接近最优情况。

在99%置信度下，当样本容量N=100时，CR散度和KL散度下的绩效损失比最大，分别为

当样本容量N=900时，两种散度下的绩效损失比最小，分别为

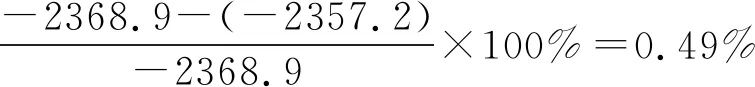
同样，在95%置信度下，样本容量N=100时，CR散度和KL散度下的绩效损失比最大，分别为

当样本容量N=900时，两种散度下的绩效损失比最小，分别为

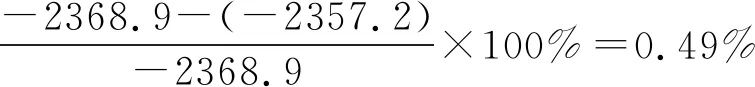
结果表明，需求分布信息的缺失虽然会导致一定的库存绩效损失，但相对于已知需求概率分布时的最优情况来说，绩效损失比值很小。进一步，由于置信水平越高，采用基于φ-散度的数据驱动方法构建的不确定集，即式(14)越精确，因此，较高置信水平下的绩效损失越小。上述结果表明，基于文中数据驱动方法得到的库存策略能够有效抑制需求不确定性扰动，具有良好的鲁棒性。特别地，对库存管理者来说，在经营过程中应注重收集日常销售数据，并选择较高的置信水平以改进决策效果。

为了进一步分析产品不同初始库存水平下的库存绩效情况，选择一组样本容量为N=600，置信度1-α=99%，并在CR散度下对库存成本进行计算。考虑两种产品的初始库存水平有如下四种情形：(1)产品1和产品2的初始库存水平均低于其各自的再订货点s1和s2；(2)产品1和产品2的初始库存水平均高于其各自的再订货点s1和s2；(3)产品1的初始库存水平高于其再订货点s1，产品2的初始库存水平低于其再订货点s2；(4)产品1的初始库存水平低于其再订货点s1，产品2的初始库存水平高于其再订货点s2。在上述四种情形下得到相应的库存成本绩效如表5所示。

表5 不同初始库存水平下的多产品库存成本绩效

由表5可知，在第1种情形下，产品1和产品2均订货，对应的库存成本绩效最高。其中，产品1订货量为11.66(96.66-85.00)，产品2订货量为41.79(147.79-100.00)；第2种情形下，产品1和产品2均不订货，对应的库存成本绩效最低；其他情况下介于两者之间。需要指出的是，在第1种情形下，库存管理者根据可能的需求情景，将对两种产品进行补货，除了产生固定订货费用外还需付出一定数量的可变采购成本，因此总成本最高；而在第2种情形下，由于初始库存水平较高，因此两种产品均不补货，在此情况下，虽有可能导致一定的缺货损失，但节省了固定订货费用和可变采购成本，因此总成本最低。进一步，对比图1中当N=600，置信度为99%时的情况发现，四种情形下的库存成本绩效显著优于初始库存水平为零时的情况。这是由于当库存初始水平为零时，管理者一方面需要付出固定订货成本，另一方面还需支付将库存补充至S水平时所导致的高昂采购成本。而在初始库存水平不为零时，即使某些情形下进行订货导致固定订货成本的发生，但可变订货成本将显著降低，从而导致总体库存成本更低。

5 结论

本文在离散随机需求概率不确定条件下，针对多产品联合库存决策问题，建立了考虑联合订货成本的单周期库存鲁棒优化模型，并给出了基于最小最大准则的鲁棒对应模型，进而证明了(s,S)策略的最优性。在仅知多产品市场需求历史数据基础上，采用基于φ-散度的数据驱动方法构建了满足一定置信度要求的未知需求概率分布不确定集，应用拉格朗日对偶方法将所建模型等价转化为易于求解的数学规划问题。最后，进行了数值计算，分析了不同散度函数和置信水平下的多产品库存绩效，结果表明，随着样本容量的增加，依据文中方法得到的鲁棒库存策略越接近真实概率分布下的情况。特别地，与真实分布下的最优情况对比发现，需求分布信息的缺失虽然会导致库存绩效损失，但损失值很小，表明基于文中方法得到的鲁棒库存策略能够有效抑制需求不确定性扰动对库存绩效的影响，具有良好的鲁棒性。进一步，可将这一方法扩展至多周期环境，并探讨如何选择合适的φ-散度来获得更优的库存策略。此外，考虑产品之间的互补或替代特性，研究如何利用基于φ-散度的数据驱动方法构建能体现产品之间具有这种互补或替代特性的需求概率分布不确定集，在此基础上制定具有鲁棒性的多产品库存决策也是未来的研究方向。