基于改进Adaptive Lasso的多工序制造过程关键质量特性识别

王 宁，张 帅，刘玉敏

(郑州大学 商学院，河南 郑州 450001)

0 引言

随着现代制造技术的发展和产品复杂程度的提高，依托先进制造技术和信息技术的进步，多工序制造过程在复杂产品制造活动中已非常普遍。在实际生产过程中，依据关键的少数和非关键的多数原则，部分质量特性对最终产品质量有显著影响，同时由于成本和技术等原因，质量控制人员无法对全部质量特性进行监控。因此，有效识别影响最终产品质量的关键质量特性是多工序制造过程质量监控与改进的关键工作。

多工序制造过程关键质量特性识别主要通过产品制造数据在线收集，利用统计回归、机器学习等数据驱动方法建立产品最终质量与质量特性间关系模型，进而识别对最终产品有显著影响的关键质量特性。如Jin等[1]通过采集过程数据以建立产品质量与过程质量波动的线性回归模型识别关键质量特性；Loose等[2]通过建立反映过程线性和非线性波动传模型识别关键质量特性。汪四水等[3]采用交叉谱分析法识别出关键因子，进而识别关键质量特性。王宁等人[4]采用偏最小二乘法消除质量特性间相关性进而识别多级制造过程关键质量特性识别。Tsung等[5]通过构建状波动传递模型，多质量特性优化分析识别关键质量特性；Wu[6]利用期望函数优化并确定关键质量特性Ding等[7]应用模式识别方法进行多工序过程质量波动传递分析, 识别造成过程波动的主要根因以确定关键质量特性。Wang等[8]观察到生产中往往会面临着信息不确定与数据不佳的情况，故提出了一种加权多属性灰色目标决策方法来帮助决策者进行关键质量特性识别，达到了很好的效果。

由于多工序制造过程的复杂性，使得过程质量特性具有高维度、小样本、强相关的特点，近年来，部分学者将关键质量特性识别抽象为通常用于处理高维数据的变量选择问题，通过统计方法从繁多的变量中选出对响应变量有很大影响的解释变量进而识别关键质量特性。闫伟[9]将信息论中的信息熵概念引入，用信息增益来判断质量特性与所属类别之间的相关性，从而有效降低质量特性维度进行有效识别；李岸达[10]将经典特征权重评价方法ReliefF算法与Wrapper算法混合起来构建ReliefF-W方法进行关键质量特性识别，能在不降低预测精度的前提下识别更少的特性；王化强[11]提出一种基于LASSO的范数选择方法，并采用SVM分类器测试所得关键特性特征子集的分类预测能力，得到了很好的效果；朱才松[12]提出一种基于改进DE算法的特征选择方法，有效的提高预测精度并降低了维度；赵喜[13]运用Monte Carlo-AHP方法对质量特性进行重要性分析并根据20/80原则提取关键质量特性。上述成果各具特色，但在解决多工序过程两个关键问题时均存在不同程度失效[14]。一是过程中各工序都存在大量质量特性，数据维度高，类型复杂，在技术、成本、环境、资源等因素约束下往往难以取得足够样本对过程建模并识别关键质量特性；另一个更为关键的是多工序过程因其组成结构和制造工艺等方面的复杂性，各工序质量特性及工序间质量特性存在多重共线性。虽然lasso及Adaptive Lasso方法可以处理多重共线性，但它们在处理强相关性变量的时候效果并不理想[17]。

因此，本文在Zou[15]，鲁庆[16]等Adaptive Lasso方法研究基础上，针对多工序串联制造过程，提出了基于改进Adaptive Lasso的关键质量特性识别方法。首先基于状态空间思想构建多工序串联制造过程关键质量特性识别模型；随后针对过程质量特性高维度，小样本特点，采用Bootstrap算法重构样本，扩大样本容量；其次引入主成分回归法(principle component regression；PCR)改进Adaptive Lasso，即采用PCR对多工序过程进行回归，用能够消除质量特性间复杂相关性的主成分回归系数βpcr替代Adaptive Lasso中常用的最小二乘回归系数βols，降低Adaptive Lasso模型的预测偏差，达到维规约目的；然后运用改进Adaptive Lasso方法构建模型并识别关键质量特性；进而通过仿真，比较lasso，Adaptive Lasso和岭回归等变量选择方法识别关键质量特性的有效性；最后，本文通过实例具体说明改进Adaptive Lasso方法应用于多工序过程关键质量特性识别的详细过程。研究结果表明，改进的Adaptive Lasso方法能够较好地处理多工序制造过程中的两个关键问题并实现关键质量特性识别，且性能优于其他方法。

1 多工序制造过程关键质量特性识别模型

本文引入状态空间思想构建多工序串联过程关键质量特性识别模型，以有效解决多工序过程中各工序质量特性对最终产品质量影响的积累和传递问题，进而识别关键质量特性。Jin和Shi[17]较早将状态空间思想应用于多工序过程建模，其核心在于各工序质量特性之间通过线性关系加以传递，将三维空间模型转化为二维的向量集，并叠加有系统性干扰[18，19]。图1是反映状态空间思想的多工序串联制造过程说明图。

图1 多工序串联制造过程说明图

相邻两工序质量特性关系模型可表示为:

Xi=Ai-1Xi-1+BiUi+εi

(1)

其中Xi=(x1i,x2i,…,xki)T表示j工序质量特性向量，Ui=(u1i,u2i,…,umi)T表示导致i工序过程失效的本工序产品质量特性向量

表示i-1工序传递的产品质量特性对i工序产品质量的影响系数矩阵

表示i工序过程失效导致的本工序产品质量特性对i工序产品质量的影响系数矩阵，εi表示系统误差。

设Y为过程最终产品质量，则根据公式(1)并通过递推迭代[17]，可得多工序质量特性关系模型:

(2)

其中Φ(.,.)是状态转移矩阵，当k>i时Φk,i=Ak-1Ak-2,…,Ai，当k=i时，Φk,k=I。本文暂不考虑系统随机误差εi，并且由于X0表示过程初始输入，不失一般性，设X0为0[17]。公式(2)简化为:

(3)

(4)

式(4)即为多工序串联制造过程关键质量特性识别模型。本文关键质量特性识别即采用改进Adaptive Lasso方法对式(4)模型进行拟合，通过变量选择筛选出对最终产品有显著影响的关键质量特性。

2 基于改进Adaptive Lasso的关键质量特性识别方法

2.1 基于Bootstrap的样本重构

多工序制造过程中，各工序都包含众多质量特性，由于质量特性类型复杂，并且在技术、资源等约束下，常难以采集到足够样本实现对过程的有效建模分析，本文拟通过Bootstrap方法对样本进行重构实现数据扩展。

Bootstrap方法由Bradley Efron于1979年提出[22]，其基本思想是假定有n个相互独立同分布的质量特性样本(xi,yi),i=1,2,…,n，对这n个样本点均匀地随机重复抽取m次，则得到m个与原样本独立同分布的自助样本。在样本分布是正态分布，及在存在严重的离群点或样本容量不够大时，Bootstrap方法相对优势明显且实用。因此，本文通过Bootstrap方法重构样本，将所得到自助样本与原样本集成，扩大样本量，然后对集成后样本使用改进Adaptive Lasso方法训练模型并识别关键质量特性。

2.2 改进Adaptive Lasso方法

(1)Lasso方法

Lasso(Least Absolute Shrinkage and Selection Operator)方法最早由Tibshirani提出并得到广泛应用，Lasso能够处理高维数据的变量选择问题，并且能够在高维空间获取稀疏线性模型，其思想原理是在最小二乘方法基础上添加L1惩罚项，即在满足回归系数绝对值之和小于一个常数的情况下，使得残差平方和达到最小，从而把某些回归系数压缩到0，增强模型的解释力[21]。

s.t. ∑j|βi|≤t

(5)

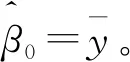
(6)

其中λ是惩罚参数且满足λ≥0。

(2)基于PCR的Adaptive Lasso改进

Lasso依据惩罚参数λ决定惩罚项的压缩程度，实现变量选择和系数估值，并通过提高偏差来降低方差，提高模型的预测精度。但Lasso也存在不足，Zou[22]证明式(6)的Lasso估计不具备oracle性质，因为它对模型中各系数β采用相同的L1惩罚项。基于此，Zou[23,24]提出Adaptive Lasso方法，对预测变量采取不同的惩罚权重系数，该方法的变量系数估计值如式(7)。

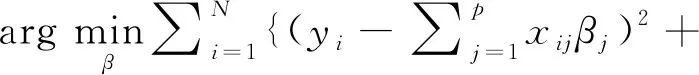
(7)

其中ωj=|βols|-γ,γ>0为权重系数，βols是对自变量与因变量使用最小二乘方法得到的回归系数，其基本思想是如果通过最小二乘回归使自变量得到较大系数值，则认为该自变量对因变量有较强解释能力，其在实际中对因变量影响相对较大，反映在自适应调整权重系数ωj上，较大回归系数使该变量的惩罚较小，因此能够提高该自变量在变量选择中被选入模型的概率，使结果更与实际相符。

但在多工序制造过程关键质量特性识别中，由于各工序质量特性及工序间质量特性存在多重共线性，并且常无法采集到远大于质量特性数量的样本量，此时采用最小二乘方法会扩大模型误差，而且回归系数的估计值也不稳定，破坏模型的稳健性[25,26]。因此本文采用PCR方法对多工序过程关键质量特性识别模型中的自变量和因变量进行建模，用βpcr代替βols。由于PCR能够在样本数量较少情况下消除变量间多重相关性，其回归系数βpcr比βols更能反映过程真实情况，进而通过自适应调整权重系数ωj=|βpcr|-γ确保关键质量特性识别的准确性和可靠性。

(3)多工序过程关键质量特性识别步骤

Step1明确多工序制造过程最终产品质量特性，分析各工序关系及工序内质量特性，通过状态空间模型构建多工序制造过程关键质量特性识别模型。

Step2依据关键质量特性识别模型，在制造过程中采集质量特性数据，形成原始质量特性数据集Data。

Step3利用Bootstrap方法对原始质量特性样本数据进行n次均匀地随机重复有放回抽样，增加样本容量，形成新的质量特性样本数据集Data_B。

Step4使用数据集Data_B对多工序关键质量特性识别模型进行PCR估计，得到主成分回归估计系数βpcr。

Step5通过主成分回归估计系数βpcr求得Adaptive Lasso中惩罚因子ωj-pcr=|βpcr|-γ。

Step6将ωj-pcr=|βpcr|-γ带入Adaptive Lasso的目标函数中替换原始的ωj，并对制造过程进行拟合。

Step7利用交叉验证，选择出来最优的回归模型，通过模型的回归系数，识别其中非0系数的质量特性即是此多工序制造过程关键质量特性。

3 仿真实验

Lasso和Adaptive Lasso是本文方法改进的基础，岭回归通过在结构风险最小化的正则化因子上使用模型参数向量的二范数形式，亦可以解决回归分析中变量间存在多重共线性等问题。为验证本文改进Adaptive Lasso方法与Lasso, Adaptive Lasso和岭回归方法在关键质量特性识别中的有效性，本文基于多工序关键质量特性识别模型仿真生成了实验数据集{X,Y}，其中X为多工序过程关键质量特性识别模型中各工序质量特性，即模型解释变量，Y为最终产品质量，即响应变量。Y的生成函数为：

(8)

同时为检验上述三种方法在质量特性间不同相关强度下的适用性，另设定corr(x1,x2)=corr(x1,x3)=…,=corr(x4,x6)=corr(x5,x6)=ρ，选取不同强度相关性ρ=0.2,0.4,0.6,0.8进行仿真实验。根据上述设定，生成原始样本数据100组，每组数据包含27个变量。利用本文所提的改进Adaptive Lasso方法，同时对比Lasso, Adaptive Lasso和岭回归方法，其回归结果如表1～表4所示，各表中带有下划线变量为关键质量特性。

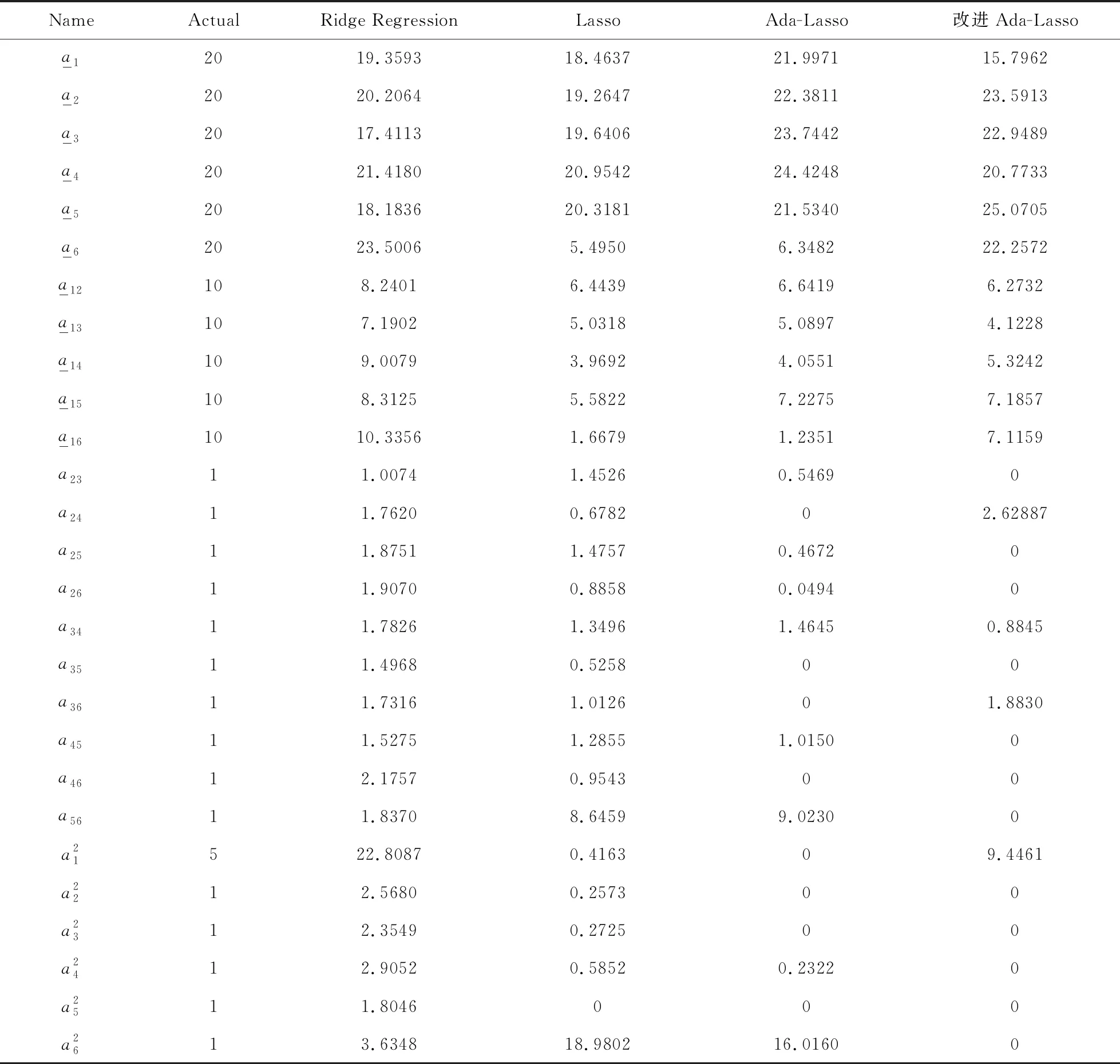
表1 质量特性相关性ρ=0.2下的回归系数比较

表2 质量特性相关性ρ=0.4的回归系数比较

表3 质量特性相关性(ρ=0.6)的回归系数比较

表4 质量特性相关性ρ=0.8的回归系数比较

由表1～4可见，改进Adaptive Lasso方法在质量特性不同相关度下均能够比其它三种方法准确有效识别关键质量特性。仅当质量特性间存在弱相关性时(ρ=0.2)，改进Adaptive Lasso方法虽能够准确识别出所有关键变量，但有其他非关键变量也被错误选择出来。其原因为，当质量特性间存在弱相关性，采用PCR方法进行回归拟合会过度处理数据造成信息丢失，导致回归系数偏差进而影响自适应调整权重系数，从而无法准确识别关键质量特性，降低改进方法的有效性。随着质量特性间相关性的增加(ρ=0.2,0.4,0.6,0.8)，本文所提方法能够准确有效地识别出所有关键变量，而另外三种方法并不能够准确识别出所有关键变量，这也从另一个侧面说明本文采用PCR处理变量间的相关性，进而利用PCR系数对Adaptive Lasso进行约束的改进方法，在具有较强相关性的多工序过程质量特性识别中更加准确有效。

为了进一步比较所提方法的识别效果，定义正确识别率和错误识别率(正确识别率=识别出的关键变量/设定的关键变量，错误识别率=识别出的非关键变量/设定的非关键变量)来评价识别效果，结果如表5所示。

表5 识别准确率比较

综合正确/错误识别率可知，在多工序制造过程关键质量特性识别中，本文所提改进adaptive Lasso方法相比于Lasso，Adaptive Lasso和岭回归方法具有较高的识别精度，特别当变量间存在较强相关性时(ρ≥0.3)，采用PCR去除变量间的相关性，并利用PCR回归系数对Adaptive Lasso中的惩罚项进行约束，可以有效准确识别多工序过程关键质量特性，识别精度可以达到100%。岭回归方法虽然正确识别率较高，但在关键特性识别中具有一定的局限性，其结果中包含所有质量特性，没有进行变量选择，因此会影响识别的准确性。

4 实例分析

现以JSYD公司铅酸蓄电池6-DZM-12型负极板生产过程为例说明本文方法的有效性。铅酸蓄电池生产过程中电极板重量一致性对最终产品质量有关键影响，因此需严格管控电极板重量。电极板核心生产过程由铸板和涂板两个连续工序组成，铸板工序是将铅粉在一定温度下通过模具生成板栅，涂板工序是在板栅上涂铅膏层后形成电极板，具体工序流程如图2所示。

图2 极板生产核心工序

4.1 极板两工序制造关键质量特性识别模型

依据铅酸蓄电池国家标准及生产工艺要求，板栅重量一致性是铸板过程的重要输出指标，极板重量是涂板过程重要质量指标，因此本文选择极板重量作为两工序最终产品质量，即因变量Y，板栅重量一致性作为铸板工序产品质量指标X1，X0表示铸板工序过程原始输入；在铸板和涂板过程中，依据工艺手册及历史经验选取铸板过程中的铅锅温度、铅勺温度、动模温度、定模温度、大片板栅重量、小片板栅重量和涂板过程中的铅粉重量、酸重量、纯水重量、出膏温度、视比重，两个工序共11个质量特性作为自变量，分别用u11,u12,u13,u14,u15,u16,u21,u22,u23,u24,u25表示。

U1=(u11,u12,u13,u14,u15,u16)T表示导致铸板工序失效的铸板工序产品质量特性向量，U2=(u21,u22,u23,u24,u25)T表示导致涂板工序失效的涂板工序产品质量特性向量，A1=[(α1,1α2,1α3,1α4,1α5,1α6,1)]表示铸板工序传递的产品质量特性对最终产品质量特性的影响系数

表示涂板工序产品质量特性对产品质量的影响系数B2=[β1,2β2,2β3,2β4,2β5,2]表示涂板工序质量特性对最终质量的影响系数。由公式(2)可得

Y=A1X1+B2U2+ε2，X1=A0X0+B1U1+ε1

设X0为0，且不考虑系统随机误差εj，则通过状态空间模型可得两工序涂板过程关键质量特性识别模型：Y=A1B1U1+B2U2。

4.2 基于改进Adaptive Lasso的关键质量特性识别

表6 实际数据的均值和方差

通过生产过程进行数据采集，共收集到109组数据，剔除有缺失项的数据，共获得有效样本79个。其中，样本数据的均值和方差如表6所示。

通过Bootstrap方法对上述采集到的原始样本数据进行重抽样扩大样本量。进而利用PCR方法对两工序质量特性进行回归拟合，得到系数估计向量βpcr=(-3.93,1.52,1.55,1.47,-6.98,-4.62,-1.16,0.85,-1.37,-2.43,102.82)，并通过βpcr求得Adaptive Lasso中惩罚因子ωj-pcr=|βpcr|-γ。

将ωj-pcr=|βpcr|-γ带入Adaptive Lasso的目标函数中替换原始的ωj，并对制造过程进行拟合。利用交叉验证，选择出来最优的回归模型，通过模型的回归系数识别此多工序制造过程关键质量特性。最终回归结果以及与Lasso， Adaptive Lasso和岭回归方法对比结果如表7所示。

表7 实例的结果比较分析

此实例为JSYD公司横向研究项目,依据生产工艺、历史经验和现场FMEA分析结果，铅勺温度、动模温度、定模温度和铅膏视比重是极板两工序制造过程中关键质量特性。表7中，Ridge Regression方法并不能够约简变量数，Adaptive Lasso方法虽然约简了质量特性“铅粉重量”，但其识别出来的关键变量分别为“出膏温度”、“动模温度”、“铅勺温度”、“铅锅温度”等，这些质量特性并不完全是实际生产过程中的关键质量特性。而本文改进Adaptive Lasso方法虽然只约简了3个非关键质量特性，但其拟合出的回归系数较大的质量特性分别为“视比重”、“铅勺温度”、“动模温度”和“定模温度”，这与实际生产过程十分吻合。

由此可见，本文所提方法相比于另外三种方法，准确识别出了铅酸蓄电池6-DZM-12型负极板两工序生产过程中关键质量特性，为JSYD公司后续实施极板过程在线监控，实现降低负极板产品次品率目标提供了重要分析依据和改进方向。

5 结论

多工序制造过程关键质量特性识别是当前先进制造广泛存在且急需解决的问题，其显著特点是多工序过程质量特性多且存在样本数小于变量数的“维度灾难”。本文通过Bootstrap重构样本，利用PCR方法改进Adaptive Lasso以解决上述难题，从仿真实验及实例结果可见，改进Adaptive Lasso方法能够准确有效地识别多工序制造过程关键质量特性，为企业质量监控及改进优化提供依据。但文章仍存在一些不足，一是本文仅讨论多工序过程中的串联模式，未研究复杂多工序过程并联结构下，如何利用本改进方法进行关键质量特性识别；二是改进Adaptive Lasso方法仅是变量选择方法中的一种；未与其它变量选择方法进行有效性比较验证；这些将在后续研究工作中不断完善深入。