层次分析法和支持向量机的电网规划方案评估与优选

王 霞，邬拥军

(内蒙古电力(集团)有限责任公司鄂尔多斯电业局，内蒙古 鄂尔多斯 017000)

0 引言

近年来，我国电网电压等级逐渐升高，具有生态环保的绿色电网吸引众多投资者，对电网规划方案合理性以及科学性需求逐渐升高。电网规划决策需综合考虑投资回报收益性、环保生态性、综合安全性、占地情况以及美观性等综合性能[1-3]。

电网规划方案评估与优选属于电网规划决策问题，电网规划决策问题是规划电网基础上综合考虑各种规划方案合理性、经济性以及发展性，通过综合评估结果选取最优规划方案，电网规划方案评估存在众多不确定性因素，影响电网规划方案评估因素较复杂，评估与优选面临巨大挑战[4-5]。程耀华等[6]研究了可再生能源并网的输电网规划方案综合评价，针对高比例可再生能源并网的特点，从可再生能源消纳压力、可再生能源的强不确定性等方向综合评价输电网规划方案；朱天曈等[7]、杨楠等[8]、李利娟等[9]提出改进TOPSIS法和德尔菲-熵权综合权重法的电网规划方案综合决策方法，该方法引入绝对理想点以及投影法改进TOPSIS法，有效提升电网规划方案决策和有效性。但是这些方法均没有考虑指标之间的差异性，致使电网规划方案评估准确性低。

为了提高电网规划方案评估的准确性，选择更优的电网规划方案，提出了基于层次分析法和支持向量机的电网规划方案评估与优选方法，并与其他方法进行了对比测试，验证本文方法的优越性。

1 层次分析法和支持向量机的电网规划方案评估与优选方法

1.1 构建电网规划方案评估的指标体系

在进行电网规划方案评估过程中，需先明确电网规划决策目标，依据所需实现目标分析相关因素，并将影响评估目标因素通过分类建立清晰的层次结构，便于最终电网规划方案的评估与优选[10]。综合优越性评分最优设置为决策目标，建立电网规划评估指标体系如图1所示。

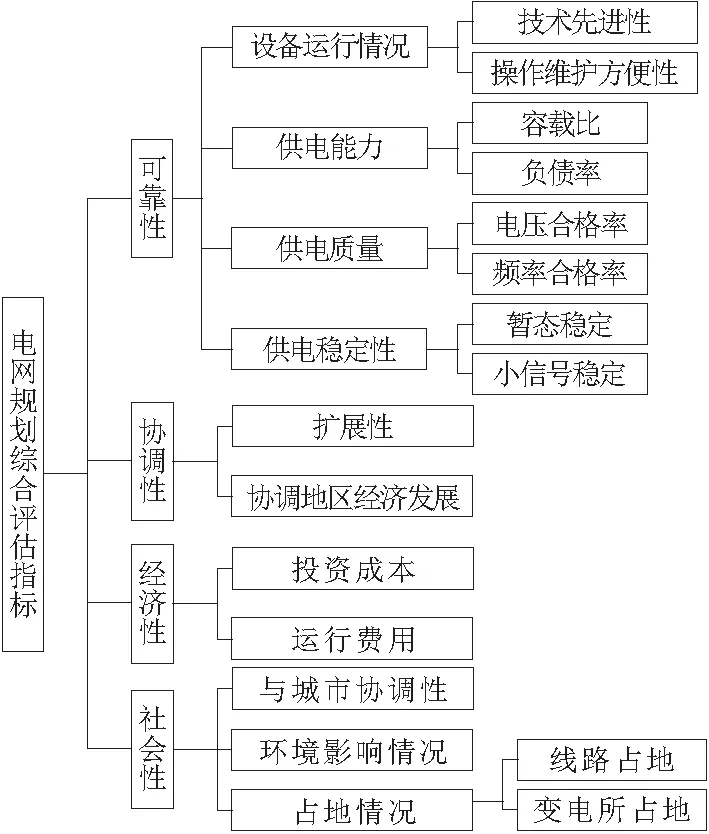
图1 电网规划方案评估指标体系次结构

由图1可知，决策目标包括可靠性、协调性、经济性以及社会性4个属性，4个属性共包含16个下层属性，将众多属性结合，建立存在关联的树状层次结构[11]。

1.2 层次方法确定电网规划方案评估的指标权值

不同的指标对电网规划方案评估结果的贡献是不相同的，为此本文引入层次分析法获取不同电网规划方案相对于总目标的综合权重，利用相对重要性评估综合权重，将不同方案相对综合优越性评分作为不同电网规划方案综合权重获取方式[12-13]。

将指标内原始数据利用固定标度体系转化至规划范格式，规划范格式便于直接比较不同指标，以上过程即为标量化，设存在2个指标分别用i以及j表示，指标i与指标j比较结果用dij表示，指标j与指标i比较结果用dji表示，可得

(1)

利用特征向量法获取不同层次评估指标相对权重，求解判断矩阵的最大特征值λmax以及特征向量W，获取权重向量(w1,w2,…,wn)。归一化处理特征向量W，获取不同层各评估指标相对于上层指标相对权重为

(2)

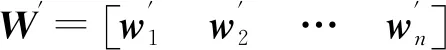
判断矩阵一致性通过最大特征值利用相容性指标检验，具体为

CI=(λmax-n)/(n-1)

(3)

CI为一致性指标；n为判断矩阵阶数。当CI<0.1以及CI≥0.1时，分别认为判断矩阵一致性可以接受以及无法接受。判断矩阵无法接受时，需重新修改判断矩阵[14]，重新计算修改后矩阵权重并再次检验判断矩阵一致性，直至一致性检验通过为止。

1.3 支持向量机建立电网规划方案评估模型

支持向量机是利用结构风险最小化原则获取理想输出的分类器，设(xi,yi)，i=1,2,…,N表示训练样本集，xi与yi分别表示支持向量机输入数据以及输出数据，支持向量机分类器将输入数据集利用非线性映射函数η()映射至高维特征空间，可得支持向量机函数模型为

f(x)=wTη(·)+b

(4)

w和b分别表示权值向量以及偏置量。

权值向量以及偏置量求解公式为：

(5)

(6)

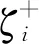
支持向量机分类器对于求解高维特征空间的最优超平面问题效果较优[15]，利用二次优化问题求解令支持向量机分类器输出数据集误差最小为

(7)

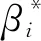
支持向量机分类器数学模型为

(8)

K()表示核函数，选取Gauss函数作为支持向量机分类器的核函数，其公式为

K(xi,xj)=exp(-‖xi-xj‖2/2h2)

(9)

h表示核函数宽度。

将利用层次分析法所确定电网规划评估指标权重作为输入样本，电网规划方案期望得分作为支持向量机输出结果，通过支持向量机回归建立电网规划方案评估模型，并根据模型对待评估的电网规划方案进行测试，输出该电网规划方案的得分，并根据得分选择最优电网规划方案。

2 电网规划方案评估与优选的实例分析

2.1 测试对象

以某地电力系统500 kV网络未来5年时间内的3种规划方案为例，采用3种电网规划方案作为测试对象，电网区域内包含节点与支路数量分别为68个以及81个，其中包含发电机节点数量为41个，电网内包括线型类型为2种。

2.2 评估结果分析

依据层次分析法确定的指标权值，采用支持向量机对3种方案进行评估结果，如图2～图5所示。由图2～图5可以看出，方案1成本最低，但安全稳定性最差；方案2与方案3均满足电网安全稳定性需求，但方案2的可靠性差，因此方案3为3种电网规划方案中最优方案。选择方案3为该电网规划的最佳方案，这与实际情况相同，实验结果验证本文方法可有效、合理评估与优选电网规划方案。

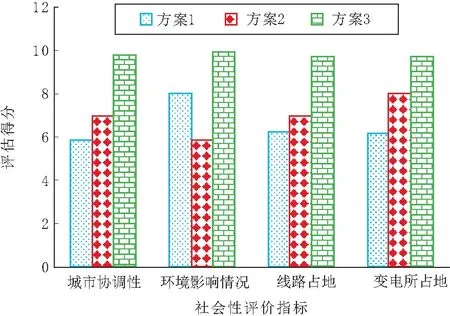
图2 社会性指标评估结果

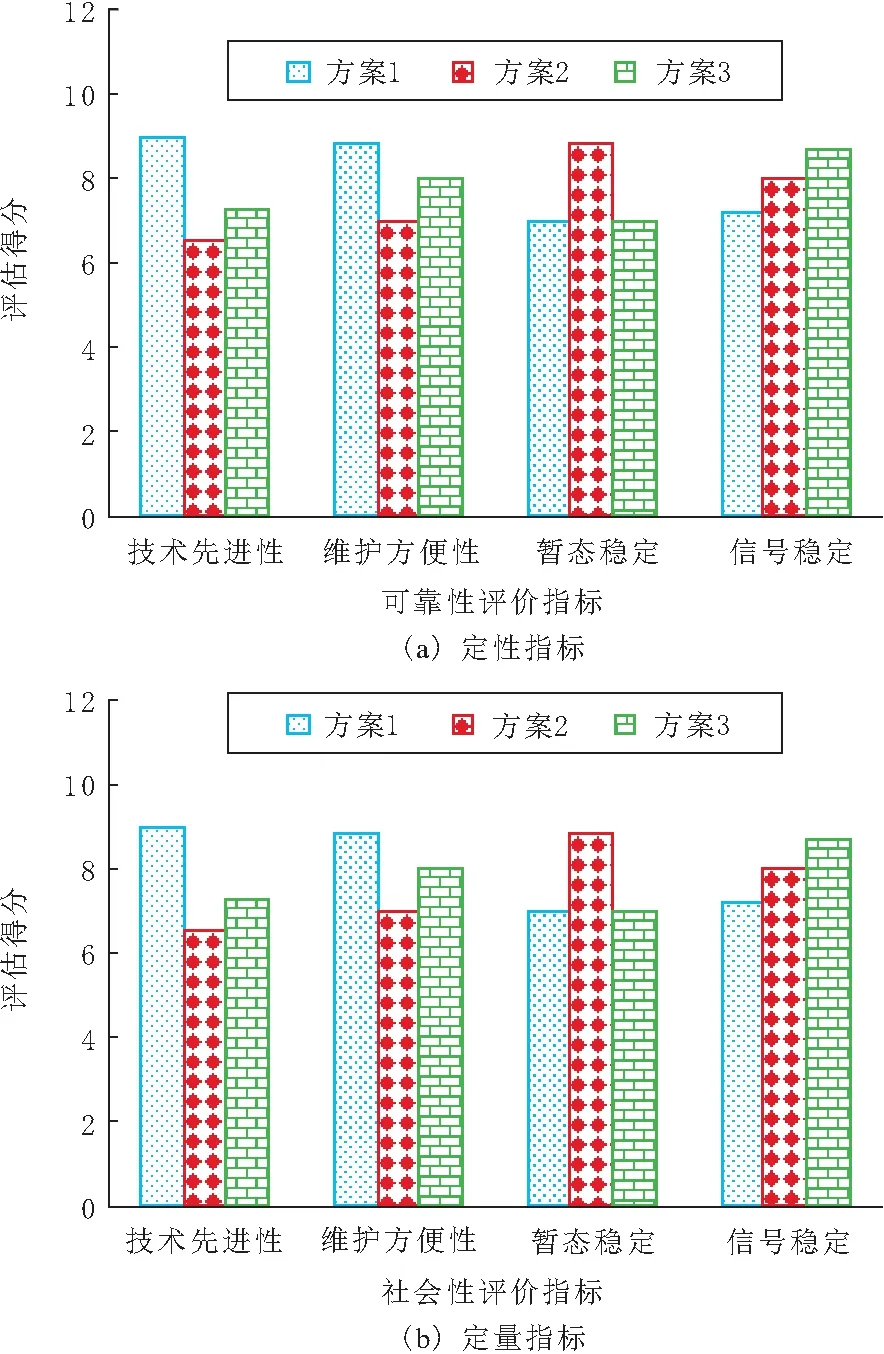
图3 可靠性指标评估结果

图4 经济性指标评估结果

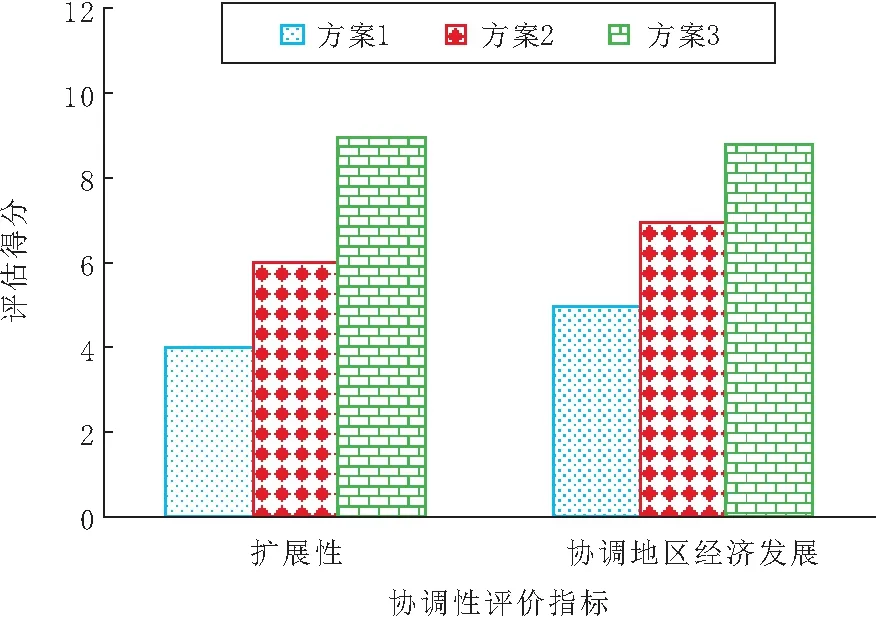
图5 适应性指标评估结果

2.3 选择最优方案的优越性分析

为验证本文方法优选电网规划方案3是否可靠，采用MATLAB仿真软件分别将3种方案应用于该500 kV电网内，采用仿真软件模拟3种电网规划方案下的电网于2018年9月—2019年8月运行情况，电网运行费用对比结果如图6所示。由图6可知，方案3所规划电网运行费用低于方案2与方案1，验证了本文方法优选的方案3具有较高的经济性。

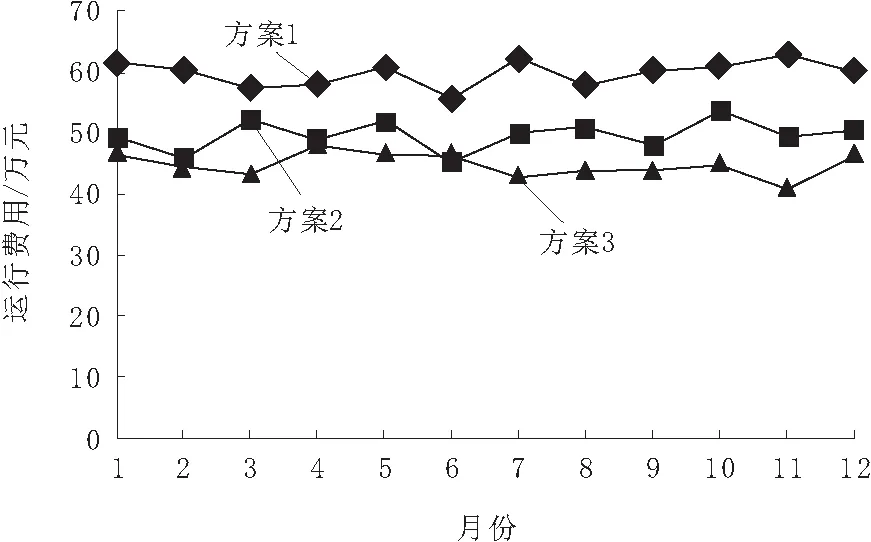
图6 3种方案运行费用对比

电网故障次数对比结果如图7所示。

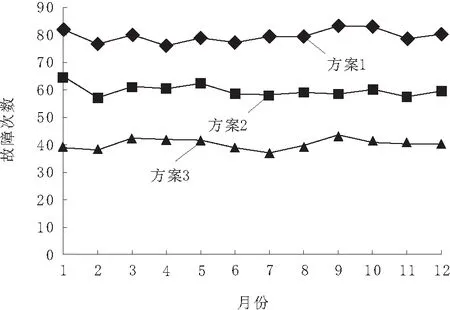
图7 3种方案故障次数对比

由图7模拟结果可以看出，采用3种方案规划电网，长期运行时方案3的电网故障次数明显低于方案1与方案2，表明方案3具有较高的运行稳定性，故障次数低，规划电网具有较高的安全性能，符合电网长期运行的安全稳定性要求。

负载率作为电网运行可靠性的重要评估指标，可有效体现电网的运行性能，电网最大负载率对比结果如图8所示。由图8可以看出，方案3最大负载率最低，明显优于方案1以及方案2，再次验证本文方法选择方案的优越性，依据评估结果可以得到最佳电网规划方案。

图8 3种方案最大负载率对比结果

3 结束语

为获得更优的电网规划方案，提出了层次分析法与支持向量机相结合的电网规划方案评估模型，利用层次分析法综合考虑电网规划方案的技术性和经济性，建立了完整的电网规划方案评估层次结构，并通过支持向量机分类器将权重求解问题转换至线性规划问题，有效提升评估效率与评估精准性，实现电网规划方案精准评估与优选。并以某地某500 kV电网为例，利用该方法有效评估3种电网规划方案，综合考虑3种规划方案的技术性以及经济性，最终选取方案3作为最优电网规划方案，通过仿真模拟软件有效验证该方法具有较高的评估有效性，可从众多方案中选取最优方案。