季节变化和温度对上海市猩红热传播的影响探究
2020-10-22张玉洁潘丽虹朱城志林支桂
张玉洁, 潘丽虹, 朱城志, 林支桂
(扬州大学 数学科学学院,扬州 225002)
猩红热(Scarlet fever),别名“灿喉痧”,是由A组β型溶血性链球菌(Group A Streptococcus,GAS)感染引起的急性呼吸道传染病,其典型症状为发热、皮疹和杨梅舌[1-2]。该病的传染源为患者和带菌者,主要经空气飞沫传播,也可经被传染的生活用品、食物、破损皮肤或产道等传播。人群普遍易感,5~15岁小儿易发病[3]。
据记载,该传染病的暴发曾对人类自身的健康和社会经济的发展造成过一定的威胁[4-5]。作为一种极易传播的传染病,近年来在我国多地呈现出了一种逐年上升的趋势,如鄂尔多斯市[6],银川[7]、合肥[8]、北京[9]等。本文基于猩红热的传播机理建立数学模型,利用数据估计系统的参数,对疫情的发展趋势进行研究,分析影响疫情发展的各种因素,为制定控制方案提供定量的决策依据。具体方法是利用上海市2012至2018年猩红热感染数据,重点考虑季节变化和气候因素建立SIS模型,研究温度、环境等对猩红热传播的影响。
1 数据搜集及整理
本文主要研究季节变化和气候因素对上海市猩红热传播的影响因素,我们首先从上海市卫生健康委员会官网(http://wsjkw.sh.gov.cn/)中获取到2012至2018年猩红热感染的数据,该数据为这7年来上海市每月猩红热感染的新增病例数如图1所示。

图1 上海市2012~2018年每月猩红热感染的新增病例数
图1中显示,上海市猩红热每年的整体发病情况基本相似,具有明显的季节性变化,一年中存在两个发病高峰,第一个高峰大致在春夏之交(4月~6月份),第二个高峰大致在秋冬之交(11月~次年1月)。因上海属亚热带季风性气候,四季分明、日照充足、雨量充沛,所以该地的季节性变化可以体现在气候环境的温度、降水量、日照长度等因素上。鉴于此,本文将着重研究当地温度对猩红热传播的影响。
我们从全国历史天气官网(http://www.tianqihoubao.com/lishi/)中获取了上海市2012至2018年月平均温度数据,如图2所示。

图2 上海市2012~2018年月平均气温统计图
以上述数据为基础,下面将利用数学模型分析猩红热传播的特征。
2 数据处理及模型分析
2.1 SIS传染病模型
首先考虑SIS模型[10]:
(1)
结合本文所研究内容,该模型中所涉及的变量分别表示为:t*为染病时间/天、S*为当天易感者人数、I*为当天感染者人数、β为感染比例系数(传染系数)、βS*I*为每天新增病例数、γ为移除率系数(恢复率)、N为被调查的总人口数。
相关资料显示,21世纪以来,上海市常住人口基本趋于稳定,于是取N为24240000人;该病疗程为6~9天,因此将恢复率γ取1/7。
现在取t为月份,I可为当月的感染人数,S为当月的易感人数,则(1)式离散为如下方程:
I(t+1)=I(t)+βS(t)I(t)-γI(t),
(2)
根据每月的新增病例数βSI及γ(=1/7),可计算出每个月感染者的人数I(t),从而得到I的实际值,如图3所示。

图3 计算得到的2012~2018年每月I(t)的实际值
利用每月新增病例数和感染者的人数I(t)可以求出β值,它是随着t时刻的变化而变化,如图4所示。
图4表明β值关于时间的曲线是上下波动的,且都在每年的5~6月和11~12月取到峰值,在每年的1~2月和7~8月取到谷值,具有较为明显的周期性变化规律,波动的周期大致为6个月。据有关资料可知[1],猩红热的传染系数的确存在周期性变化的规律。因此我们将依托传染系数研究影响猩红热传播的因素。
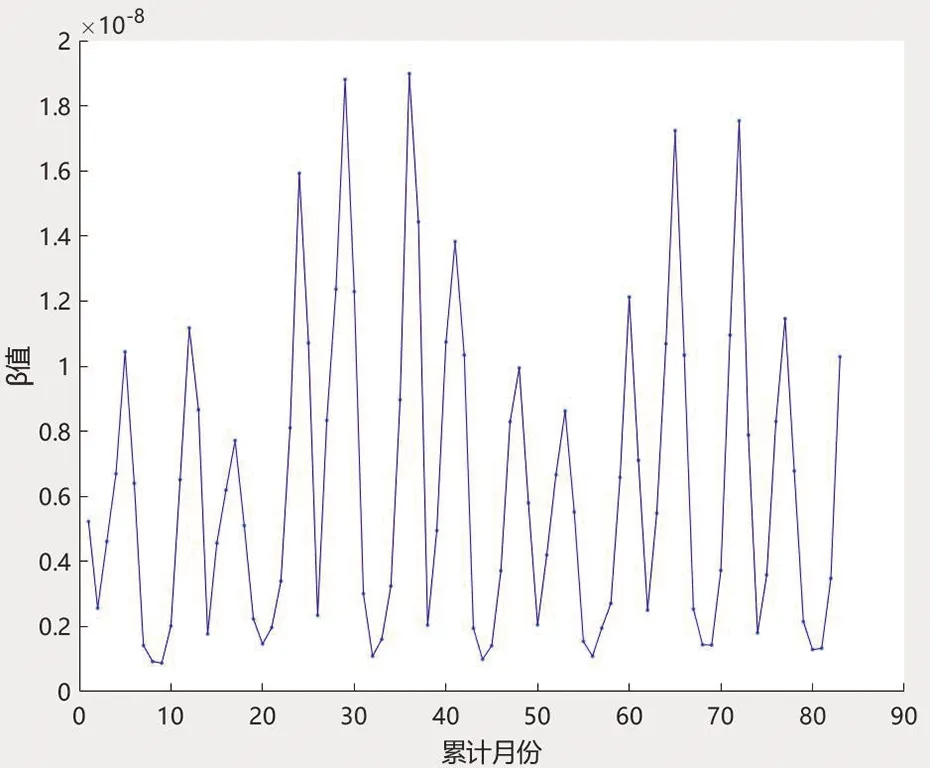
图4 计算得到的2012—2018年β的实际值
2.2 传染系数的周期性变化拟合
首先考虑单周期变化。将2012—2018年β的值进行频谱分析,得到如图5所示结果。
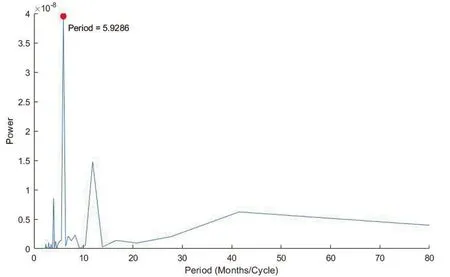
图5 单周期的频谱分析图
该频谱分析图显示其变化周期为5.9286个月,我们取其近似值6个月(即半年)为一个周期,进行单周期变化的研究。结合非线性拟合的方法拟合出如下表达式:
7.60898*10-9,
(3)
如图6所示。

图6 初步拟合的单周期的传染系数图
该图中的拟合曲线,整体趋势与实际值一致,周期为半年。但拟合曲线的振幅受实际值中的个别点(已标注为实心点)影响较大,引起了较大误差。这些误差可能是这几个时刻由于大型活动导致的人员流动增加所致,如果不考虑这几个特殊点并进行二次改进,结果如图7所示。
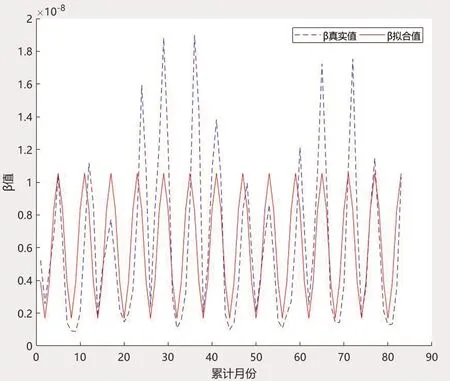
图7 改进拟合的单周期的传染系数图
图7中拟合曲线的表达式为:
(4)
较图6,除去上述特殊点之后,拟合曲线的振幅有所下降,使得拟合度更高。
再考虑叠加的周期变化。观察图7发现,峰值也存在着周期性变化,将所有的峰值进行频谱分析,得到如图8所示结果。
图8表明6个峰值为一个周期,由于一年内有两个峰值,所以6个峰值对应的时长为3年,即周期为3年。因此我们考虑拟合一个叠加周期的表达式,利用非线性拟合的方法拟合出该表达式为:
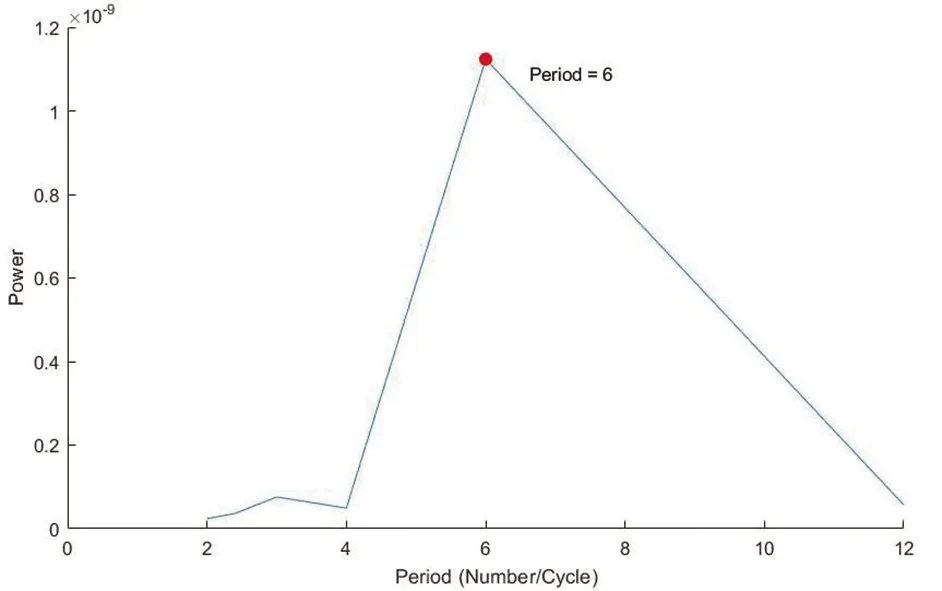
图8 峰值的频谱分析图
(5)
拟合曲线如图9所示。
对比图7与图9,叠加周期的拟合将上述特殊时刻的实际值纳入考虑范围,第一周期为半年,第二周期为3年,其拟合度更高。下面将在此基础上引入温度及环境的影响做出进一步的改进。
2.3 温度对传染系数的影响
由图2已知,猩红热在一年中感染存在双高峰,分别为5月份和12月份。考虑到温度的影响,我们对表达式(5)进行修改:
(6)
其中a、b为参数,T为t时刻的温度。根据图2平均温度的变化,可用非线性拟合方法拟合出一个温度的表达式为:
(7)
对上述表达式(6)进行拟合得:
(8)
其拟合曲线如图10所示。
图10中的拟合曲线,几个谷值相较于图9中的谷值更接近于实际值,可以发现,温度对传染系数存在明显的影响。

图9 拟合的双周期的传染系数图

图10 温度影响下的双周期的传染系数拟合图
2.4 每月感染人数I(t)的理论值与实际值的比较
基于上述对传染系数β的研究,我们将拟合出来的β的表达式(7)代入模型(1)得到每月感染人数的理论值,其理论值与实际值的比较如图11所示。

图11 I(t)的理论值与真实值的对比图
由图11,我们可以看出每月感染人数的理论值与实际值重合度较高,且通过残差分析得出其拟合的相关系数为0.9280,再次说明上述方法的拟合度较高,从而证实本文研究的合理性,即季节变化与温度对猩红热的传播有影响,且猩红热的传染系数具有双周期的变化规律。
3 结语
目前已经有很多方法和模型用来分析猩红热疫情流行病学特征,如以泊松分布作为概率模型的时空扫描法[3],描述性分析法[2],自回归移动平均混合模型[7]等。本文我们利用SIS传染病模型计算出上海市猩红热传染系数的实际值,着重考察传染系数的变化,根据图形特点,首先给出一个单周期的表达式,然后拟合出一个较为合适的叠加周期表达式,最后引入温度因素,对叠加周期表达式进行了修改,利用数学软件初步得到了传染系数的周期性变化,最终将传染系数的拟合表达式进行回代,对比感染人数的理论值与真实值,从而说明了季节和温度对猩红热传播的影响,具体表现为在每年春夏之交(4~6月)、秋冬之交(11~次年1月)猩红热的感染人数有明显的增加。借此提醒广大人群尤其5~15岁小儿,在春夏之交以及秋冬之交特别关注气温变化,做到防寒保暖,降低感染猩红热的可能性。
当然作为传染病,政府的干预、媒体的报道、人口的流动等因素均会对猩红热疫情产生重要的影响,本文着重从季节变化和气候因素中的温度两个方面进行了研究,其结果仍存在一定的局限性,我们将在此基础上进一步完善模型,为政府精准做出防疫措施,媒体适时宣传引导群众提供数据支持。
