基于新课程理念的命题考查策略

王国韬

（福州市鼓楼第一中心小学，福建 福州 350001）

《义务教育数学课程标准（2011 年版）》指出：“数学评价是为了全面了解学生的数学学习的过程和结果，激励学生的学习和改进教师的教学。”教学质量检测是数学评价体系中的一个重要组成部分，而试卷的命题则是教学的“指挥棒”。下面结合试题命制经验，谈谈符合新理念的命题策略。

一、基于知识技能的考查，指向概念的理解

学生掌握数学知识，应以理解为基础，并在知识的应用中不断巩固和深化。以往基础知识、技能的考查，主要体现在对概念形成的结果的考查，往往忽视概念形成的过程。教师在命题设计时，既要考查概念形成的过程，又要关注对概念的理解、应用。可以通过对相似概念的甄别、判断，形成对其本质的理解。

例1 在正方形、等腰三角形、平行四边形、长方形中，找出一个与众不同的图形，并说明理由。

这道题是考查图形面积的计算、轴对称图形、图形的特征、特性等多个概念的开放题。学生可以选择平行四边形，原因是平行四边形不是轴对称图形；也可以选择等腰三角形，因为其他图形都是四边形；或从求面积计算的角度看，其他三个图形面积都是底乘高。学生通过甄别判断，对四个平面图形间的异同产生更深刻的理解。一道题既考查了学生问题解决的能力，又培养了学生的创新力。

二、基于解决问题的考查，指向应用能力的培养

弗赖登塔尔认为，“数学教育应该源于现实，用于现实”。［1］将数学知识和技能融入“现实生活情境”，或让学生置身于“身边的数学”问题，能够更好地考查学生解决问题的能力，提升其应用意识。命题时，教师将知识点融合到图文、时政要闻、游戏活动等生活媒介中，不仅增强学生对数学本质的理解，还激发学生求新求异的学习欲望，使其在“生活经验”之下，学会合理预测和决策，提升数学应用能力。

（一）根据经验，发展推理能力

例2 下列几组数据中，哪一组能组成一个三角形衣服架（ ）。

A.13cm，14cm，15cm B.11cm，11cm，20cm

C.11cm，11cm，11cm

本题选择衣服架作为载体，新颖别致。将现实生活中的事物作为试题背景，构造出的试题往往能成为试卷中的亮点。本题主要的考查点，是对衣服架这个三角形形状和边的关系的特殊性的考查。试题中呈现的三组数据都能组成三角形，但组成的形状、大小各不相同。其中，A 数据为一般三角形，C 数据为等边三角形，这两组数据显然不能匹配“衣服架”这个生活素材，因此只能选择B 选项的等腰三角形，且还要是钝角三角形。命题者紧扣学生在学习过程中可能存在认知难点、薄弱点，借用生活事物进行命题设计，学生在解决问题中，真切地感受到数学源自生活。

（二）根据问题，寻求不同策略

例3 庆“六一”活动，各商城进行打折促销，原价299 元的书包，现按活动价出售。甲商场每满100 元立减20 元；乙商场原价打八折；丙商场原价打九折，持有VIP 卡再打九折。如果你是顾客，你会选择那种优惠方案，请说明理由。

上述命题，一方面，让学生体会到用数学思维寻求解决问题的不同策略；［2］另一方面，使学生在情境驱动中感悟到数学不再是枯燥的“数字”，而有其独特的“生活味”，进而形成用数学眼光观察、思考、表达的核心学习力。

（三）根据条件，选择合适解法

例4 我国规定家庭用电计费方式采用阶梯式收费方式：0-150（千瓦时），每千瓦时收费0.45 元；151-400（千瓦时），每千瓦时收费0.55 元；401（千瓦时）以上，每千瓦时收费0.85 元。王老师家8 月份用电846千瓦时，共计使用电费多少元？

此类命题是生活中常见的数学问题，但并非每个人都有留心探究。此类命题多以大量的信息呈现，考查学生获取信息、阅读分析的能力。要求学生在解决问题时，要先对条件进行分类，然后从问题入手进行分析，最后根据问题分类解答。［2］类似的题目还有阶梯式水费、工资缴税等。

三、基于运算能力的考查，指向算理的理解和运用

运算能力主要是指根据法则和运算律正确地计算的能力，其主要考查形式是计算题。在命题时，教师应摆脱“重算法，重结果”的陈旧观念，注重考查学生对理解算理及寻求合理简洁的运算途径解决问题的水平。

（一）重视算理理解，以理驭法

例5 有46 支铅笔，每个小朋友分2 支，可以分给多少个小朋友？小亮用竖式计算出了结果，竖式中箭头所指部分表示的意思是（ ）。

A.已经分掉了2 支

B.已经分掉了4 支

C.已经分掉了40 支

D.已经分掉了46 支

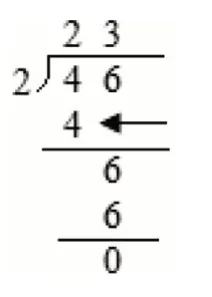
例题，若只考核46÷2 的计算，则只停留在对算法的考查。本道例题的设计，则凸显学生在学习过程中对算理的理解，明确计算时每一步的实际意义。［3］

（二）重视算法多样，提升技能

例6 用计算器计算28×36 时，按键“6”坏了，下面算法正确的是（ ）。

A.28×4×9 B.28×35+1

C.36×30-2 D.28×30＋28×6

试题借助情境，为学生展示28×36 的多种算法。既关注技能的形成，又呈现学生在计算学习过程中的多样化策略，在思考与对比中，提升运算技能。

四、基于探究能力的考查，指向思想方法的提炼

课标指出：通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想和基本活动经验。可见，学生对数学知识更高层次的抽象与概括，就是让其经历独立思考、自主探索、分析比较等活动过程，继而逐步感悟基本的数学思想，积累活动经验。

例8

本题旨在考查学生能否运用从简单入手的方法，探索简单的圆片层数与总个数之间的关系，推算出圆片层数与总个数之间的关系情况。既考查学生在探索规律中体现出的推理能力，又落实教师在课堂教学中对学习过程的重视情况，渗透数学思考的思想和方法，避免只求解题结果，忽视学习过程的现象。