小学数学结构化学习的优化路径

芮金芳

（江苏省溧阳市平桥小学）

结构，在《现代汉语词典》中解释为“组成整体的各部分的搭配和序列”。皮亚杰认为，认识不仅具有结构，而且认识是一个由从低级到高级不断建构、完善结构的过程。布鲁纳则认为，一个人在学习历程中，不是简单地把概念、信息、知识堆砌起来，各种知识之间充满纵横交错的复杂联系，是一个动态的结构。小学数学结构化学习是指在大单元整合视野下，基于学生已有认知经验建构，生长动态化的知识结构体系，促进学生个性化认知的学习过程。在这个过程中，学生整体感悟知识结构，促进深度学习发生，积淀数学核心素养。当前，在小学数学课堂中存在知识零散、学习浅层、思维离散等问题。在教学中，教师应引导学生养成整体、系统、深度、结构化的数学学习习惯。要达成这样的目标，需要找到小学数学结构化学习的优化路径。

一、关联核心要素，建构“块知识”的整体结构

数学概念是对数量关系、空间形式特征的概括，它是同类事物本质特征联合起来所形成的一种属性。数学概念的形成是抽象、理性的。要让学生理解抽象的数学概念，需要把诸多相关联的核心要素进行一定的意义建构，从而获得对概念本质的理解，形成良好的整体认知结构。

如在教学“认识分数”一课时，一位教师提供了不同形状的图形，让学生折一折、涂一涂，表示出他们的二分之一。这位教师精选结构化的资源素材，用核心问题引领学生发现知识之间的共同要素，引导学生提炼二分之一的本质属性。在这个过程中，学生结构化地整体理解和掌握了分数的知识。

图1

师：如图1，这些图形的折法不同，涂色部分的形状也不一样，为什么都能表示是这张长方形纸的二分之一呢？

生：这些折法都是把一张长方形的纸平均分成两份，涂色部分是其中的1份。所以，涂色部分都是长方形的二分之一。

师：除了这些折法，还有其他折法也能表示出这张长方形纸的二分之一吗？

生：只要沿着长方形的中心点任意分成2份，都可以表示它的二分之一。（如图2）

图2

图3

师：如图3，这些图形形状各不相同，涂色部分的形状也不一样，为什么涂色部分也都能用二分之一表示呢？

生：不管图形的形状如何，只要把它平均分成2份，涂色部分是其中的1份，就可以用二分之一来表示。

学生在教师提供的丰富多样、具有结构化资源的素材中，从两个维度即同一组内图形大小、形状、颜色完全相同和不同组内大小、形状、颜色不相同进行动作表征和图形表征，在多次深度比较辨析中逐步剥离，去除分数次要的、非本质的特性，保留聚焦“只要平均分成2份，每份就是它的二分之一”符号表征的核心要义。在具有结构性、整体性、关联性素材的利用和比较中，学生对“二分之一”这个分数核心概念的意义建构，逐渐从模糊走向清晰、从单一走向多维、从零散走向整体，形成了比较完备的整体认知结构，也为后续进一步学习“认识一个整体的几分之一”“分数的意义”奠定了基础。

二、深度理解算理，建构“类知识”的方法结构

学习是学生基于自身认知经验基础上的一种再认识、再提升、再生长。在整个小学阶段的计算学习中，如何实现算理理解与算法建构的有机统一，一直是整数、小数、分数运算中的核心问题。学生对于算理和算法的学习，主要体现在口算、估算、笔算中。笔算的算理和口算基本一致，但算法往往需要经历由“原始”到简洁的规范过程，而且稍复杂的笔算算理与算法都是在简单笔算基础上延伸、发展而来的。

基于这样的认识，在教学“两位数乘两位数笔算乘法（不进位）”时，我立足学生已有的口算经验，通过对比和迁移，丰富了学生对笔算乘法类结构特征的整体认识和结构把握，架构起了多样算法之间的内在意义联结。

如学习24×12时，我利用导学单呈现了口算、点子图、竖式计算的三种方法。

拆分法：

24×10=240；24×6=144；

24×2=48；144×2=288。

240+48=288。

画点子图法： 竖式计算法：

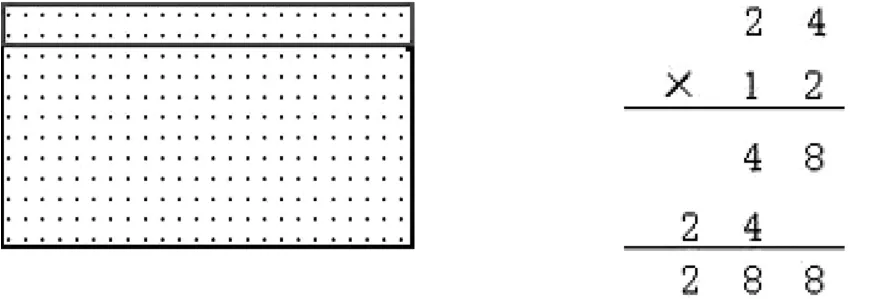
不同的算法将学生原有计算经验中“先拆再合”的思想充分展示了出来，使学生在结构化对比、沟通中发现了这些不同算法之间的内在关联。点子图直观地还原出了两位数笔算乘法的算理意义，以形助数，帮助学生以直观可视的方式理解了背后的算理。同时，它与口算中的“分步式”完全相同，帮助学生打通了“图式—分步式—竖式”之间的结构通道，在整体比较中找到了各算法之间的融通点，实现了由明确算理到建构算法的自然过渡。（如图4）

图4

在形成两位数笔算乘法一般计算方法后，我引导学生回顾以前学过的“两位数乘一位数笔算乘法”，并提问：如果是三位数乘两位数该怎样算？任意数和两位数相乘呢？任意数和三位数相乘呢？（如图5）

图5

皮亚杰曾说：“全部数学都可以按照结构的建构来考虑，而且这种建构始终是开放的……这种结构或者正在形成更强的结构，或者由更强的结构来予以结构化。”学生从乘数一位数出发，在类推联想到两位数、三位数、甚至更多位数的计算中，在迁移与对比中，实现了整数乘法笔算的横向整合，形成了整数笔算乘法一般化的“算理”结构模型，构建了笔算乘法的网状关联结构，加深了对笔算乘法算理本质的深度理解。

三、体悟策略思想，建构“群知识”的意义结构

“解决问题的策略”这个板块的内容是从三年级开始每册安排的策略主题学习。具体内容分布如表1。

表1 “解决问题的策略”内容分布表

教材一共编排了8次“解决问题的策略”专题学习，虽然策略学习内容不同，但教材在策略教学的体系编排结构、内容展开、过程推进中都具有类似的关联度。

（一）教材编排结构上的关联性

不管是哪一种策略教学，教材都按照解决问题的四大板块展开，即“理解题意—分析关系—自主解答—回顾反思”，引导学生经历分析和思考问题的全过程。正如波利亚在《怎样解题》一书中提到，解题过程一般包括四个步骤：弄清问题、拟定计划、实施计划、回顾反思。

（二）学习内容展开上的关联性

以五年级上册“一一列举的策略”为例。首先，以“王大伯围栅栏”典型实际问题情境切入，激发学生了解这个策略是什么策略、它有什么作用、具体该怎样实施的学习内需；其次，结合具体数量关系的分析思考，逐步内化“一一列举”策略，初步感悟在解决什么问题时可以运用这一策略；最后，随着策略运用解决问题中经验的逐步累积，学生自觉形成灵活选择策略解决问题的意识，并能学会自我监控回望策略运用的全过程。这样的策略学习内容展开逻辑，同样适用于其他策略的学习。

（三）策略推进过程中的关联性

学生解决问题策略的形成不是一蹴而就的，它是一个潜移默化、循序渐进的过程。所以，不管哪种策略的学习，都需要贯穿“策略需要—策略感知—策略体验—策略形成—策略应用”这一学习线索，在策略学习中，学生只有将自身的学习经历提炼上升为策略经验，方能充分体验与深刻理解不同策略的本质要义。

布鲁纳认为，掌握事物的结构，就是以使许多别的东西与它有意义地联系起来的方式去理解它。学习结构就是了解他们之间是怎样相互关联的。在解决问题策略学习中我发现，任何一种策略学习都不是孤零零的一个节点，如果利用关联整合视角发现策略教学中的联系，就能组建一个更大的策略群学习结构网络，由点及面、由浅入深地建立策略学习的生长序列，架构不同策略之间的意义联结，促进策略学习中知识、经验、思想的深度融合。

四、积淀反思素养，建构“类思想”的循环结构

结构化学习，不仅要引导学生感悟数学知识之间的显性结构，更要领悟方法形成中的隐形思维结构，生长出结构化学习过程中的关联性思维、整体性思维、系统性思维、逻辑性思维，并拓展应用到新的数学学习中。这样，才能引导学生逐步形成数学核心素养。

美国心理学家波斯纳认为，没有反思的经验是狭隘的经验，最多只能是肤浅的知识。结构化学习给学生提供了整体建构、寻求关联、逻辑判断、主动创造的学习历程和思维进阶空间，在反思中有助于深化学生对数学知识和数学思维方式的再认识、再思考、再理解、再创造。同时，有助于促进学生思维整体结构的深层次运行，促进学生元认知能力的发展和提升。

在学生学习了“解决问题的策略（画图）”后，教师要引领学生回望审视解决问题的全过程，思考：这个解决问题的策略是什么？这个策略是怎样解决这一类和差实际问题的？我们是怎样想到画图的？为什么选择画线段图？画图时我们要注意什么？画图对我们进一步理解、分析、思考解决问题有什么好处？同时，要回顾“在以前的学习中，有哪些地方运用画图策略来解决问题的？”还可以延伸至“数学中的画图策略除了今天学习的画线段图还有其他的吗？”“除了画图策略还有其他解决问题的策略吗？”“今天研究的数学上的画图策略与美术课中画图有什么异同点？”这样瞻前顾后地追问，将学生原先积累的运用画图策略分析、思考、解决问题的零散经验汇总聚合，有助于学生从以往的学习经历中剥离、提炼出数学思想方法和应用策略，形成具有迁移作用的策略体验。同时，能将这种体验延伸至后续的其他解决问题的策略学习中，将学生的认知方法、结构不断丰富、完善、打开，形成一个开放、循环、流动的结构，真正触发学生思维的深度生长。

结构化学习，需要教师在教学中形成结构性思维，以整体关联的视角、开放动态的内容、连续循环的过程、迁移生长的反思，不断促进学生结构化学习的自然发生，并在知识的理解、整合、关联、迁移中培养学生的结构化思维，以真正促进高阶思维的形成，实现优质化的深度学习。