考虑橡胶质量的两级局域共振子梁的振动研究

2020-10-21同志学齐小军李丽霞

机械设计与制造 2020年10期

同志学，齐小军，李丽霞

（西安建筑科技大学机电工程学院，陕西西安 710055）

1 引言

声子晶体的出现为梁的振动控制提供了新的思路。声子晶体是一种具有带隙特性的弹性常数及密度周期分布的材料或结构。在带隙频率范围内，弹性波的传播被抑制，这种特性使得在带隙频率范围内的振动被削弱，为振动控制领域提供了新的想法。声子晶体产生带隙的机理有两种：布拉格散射机理[1-3]和局域共振机理[4-7]。其中，布拉格散射型声子晶体的带隙频率所对应的波长与晶格常数处于同一数量级，其一般需要较大的晶格常数才能获得低频带隙，实现在低频范围的减振。2000 年，局域共振型声子晶体首次被提出[7]，其实现了“小尺寸控制大波长”，可以在较小的晶格常数下获得低频振动带隙，突破了布拉格散射机理的限制。局域共振型声子晶体为低频振动控制开拓了新局面。

目前，一些学者将声子晶体的局域共振思想引入到结构设计中，提出在梁、杆或轴上周期性地附加单级局域共振子结构，发现了局域共振结构可以获得低频范围内的振动带隙，实现了振动控制[8-10]。然而，这些研究全部专注于单个带隙，这对于在实际工程中多个频率范围内的振动控制具有局限性。近年来，多局域共振子的结构被提出，发现其具有比单级局域共振子结构更低的带隙起始频率和更宽更丰富的第二振动带隙[11]。但是，其在附加较大质量的多局域共振子时获得的第一振动带隙仍然较窄，第一和第二带隙覆盖的频率范围较小。

传递矩阵法被广泛应用于一维局域共振型声子晶体结构的带隙计算之中[12]。目前，国内外学者引入类似弹簧振子结构的简化原理模型研究了局域共振子结构的带隙特性[11]。但是，在利用传递矩阵法时将局域共振子中的橡胶简化为无质量的弹簧，忽略了橡胶质量的影响，这使得获得的带隙结果与有限元法的计算的传输特性曲线结果出现了偏差。

首先给出一种两级局域共振子欧拉梁，考虑局域共振子中橡胶的质量，采用传递矩阵法研究了该结构的振动带隙特性。进一步分析该算法的收敛性。采用有限元法计算了有限周期结构的传输特性曲线。最后分析了材料密度对振动带隙的影响。

2 考虑离散弹簧质量的传递矩阵法

考虑橡胶质量的两级局域共振子欧拉梁的简化原理模型，如图1 所示。其将每一级由一个橡胶和散射体组成的局域共振子按原理简化为一个带质量的弹簧和集中质量块。图1 所示第一级橡胶的质量为MS1，径向刚度为K1。第二级橡胶的质量为MS2，径向刚度为K2；第一级和第二级散射体的质量分别为M1、M2。该欧拉梁的晶格常数为a。

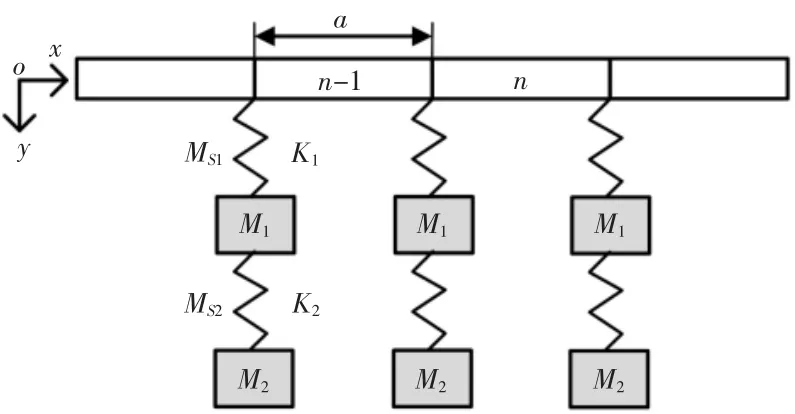
图1 考虑橡胶质量的两级局域共振子欧拉梁的简化原理模型Fig.1 Simplified Principle Model of Two-Stage Local Resonators Euler Beam Considering Rubber Mass

假设轴线只有y 方向的横向位移y（x，t），则欧拉梁的横向位移y（x，t）满足下列弯曲振动方程[8]：

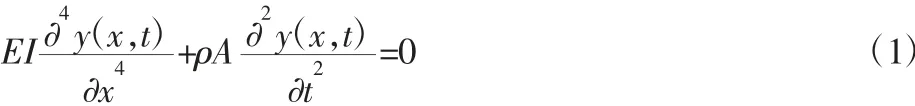
式中：ρ，E—密度和弹性模量；A—梁的截面积；I—截面二次矩，梁的横向位移为y（x,t），设横向位移y（x,t）=X（x）exp（iωt），其中X（x）为振幅，ω 为角频率。对于第n 段梁，弯曲振动解可写为如下形式[8]：

在宫廷文化中，狮子则代表着至高无上的帝王威仪，立于宫殿朝堂之前，见证着赫赫皇权。在民间习俗中，狮子同样是吉祥的象征，是能辟邪的瑞兽，有驱邪、保平安的作用。因此在民间可以常常看到气派的府宅大门前左右分别立有一狮子，铜门环上钉有狮面图案。南北方的重要节假日都有舞狮的民俗活动，还有众多各异的狮王庙，皆可以看出狮子在传统文化中有着举足轻重的地位。

该结构的考虑离散弹簧质量的传递矩阵法的简化原理模型，如图2 所示。根据连续质量离散化分布的思想，将第一级和第二级橡胶分别均匀地离散为N1个相同的和N2个相同的弹簧振子串联系统。其中，第一级和第二级橡胶的质量分别离散为N1个相同质量的振子和N2个相同质量的振子；第一级和第二级橡胶的径向刚度分别等效为N1个串联弹簧和N2个串联弹簧的等效刚度；第一级橡胶的第N1个和第二级橡胶的第N2个振子质量分别附加到第一级和第二级散射体质量上。因此，两级局域共振子结构的简化原理模型可以被看作N（N=N1+N2）个弹簧振子的串联系统。

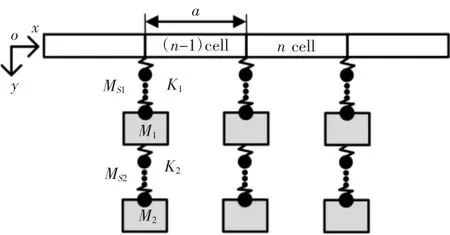
图2 两级局域共振子欧拉梁的考虑离散弹簧质量的传递矩阵法的简化原理模型Fig.2 Simplified Principle Model for Transfer Matrix Method of Two-Stage Local Resonators Euler Beam Considering Discrete Spring Mass

则第i（i=1，2，…，N）个弹簧振子的弹簧刚度ki为：

第i 个弹簧振子的质量mi为：

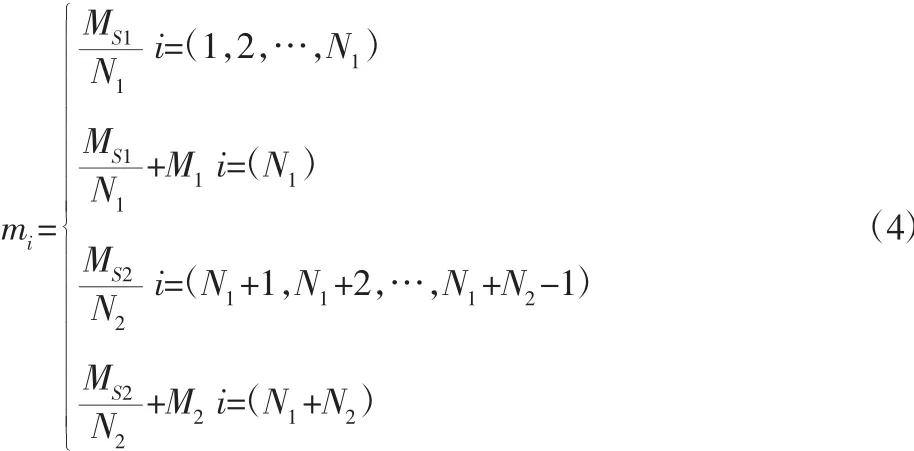
在第n 个原胞的局域共振子中第i 个弹簧振子的纵向位移为Zni（t）=Vniexp（iωt），其中，Vn是振幅。第一个、第i（i=2，3，…，N-1）个和第N 个弹簧振子的运动方程分别为：

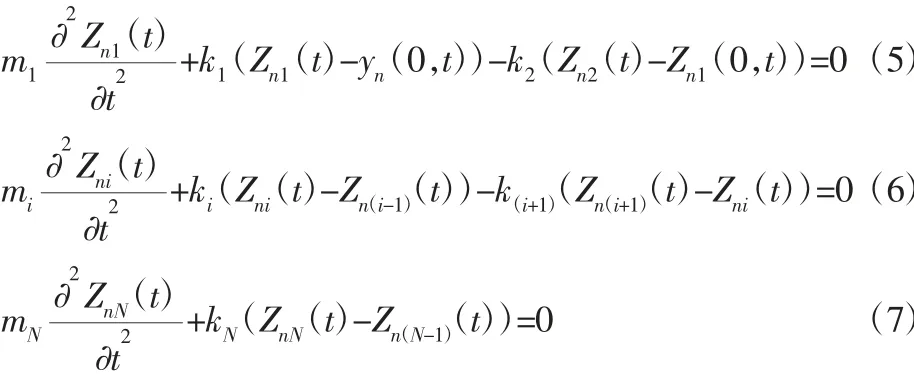
由第（n-1）个原胞和第n 个原胞之间的位移、倾角、弯矩及剪切力连续得到：

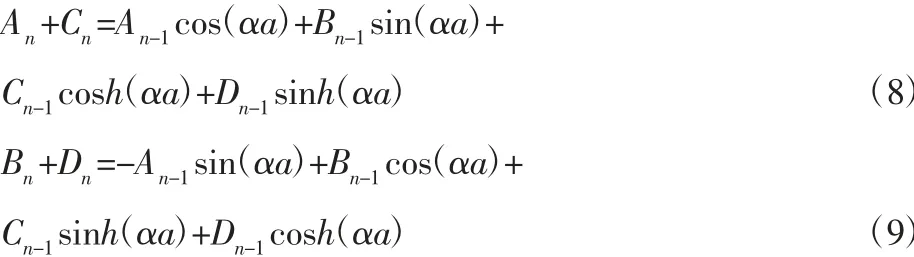
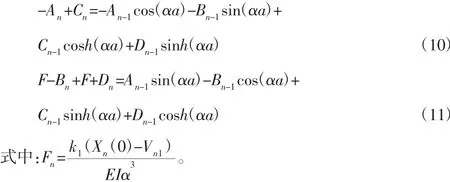
因此，式（8）～式（11）写成如下的矩阵形式：

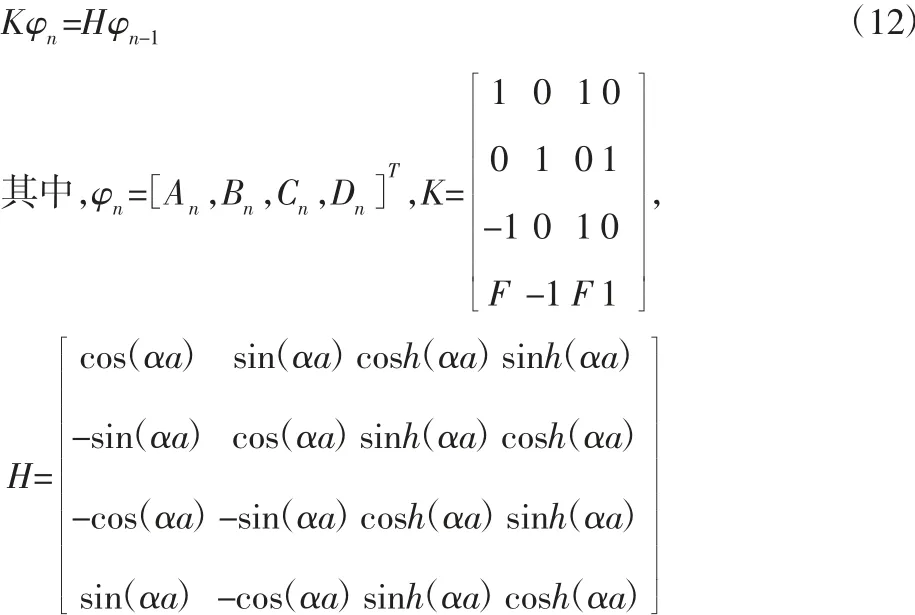
由于梁是无限周期，所以矢量φn必须满足Bloch 定理：

式中：q—波矢。

这个问题可以转化为特征值矩阵方程：

其中，T=K-1H，I 为4×4 的单位矩阵。通过求解矩阵的特征值，即可求得色散关系曲线。对于给定的ω 值，方程（14）得出相应的q 值。如果q 值有虚部，则相对应的波传播不能通过梁。q 的虚部表示带隙内波的衰减特性。

3 数值计算与讨论

两级局域共振子欧拉梁的结构示意图，如图3 所示。两级局域共振子由橡胶环和环状散射体交替组成，每级局域共振子包括一个橡胶环和一个包覆在橡胶环外的环状散射体。梁的内径为r0=0.007m，外径为r1=0.01m。两级局域共振结构的结构参数为：r2=0.015m，r3=0.0195m，r4=0.0245m，r5=0.029m。梁的材料为铝，两级散射体的材料都为铜，具体的材料参数，如表1 所示。周期结构的晶格常数为a=0.05m。所有环的长度为l=0.01m。

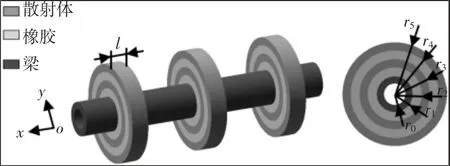
图3 两级局域共振子欧拉梁的结构示意图Fig.3 Structure Diagram of Two-Stage Local Resonators Euler Beam

对于第一级橡胶环的径向刚度为[13]：

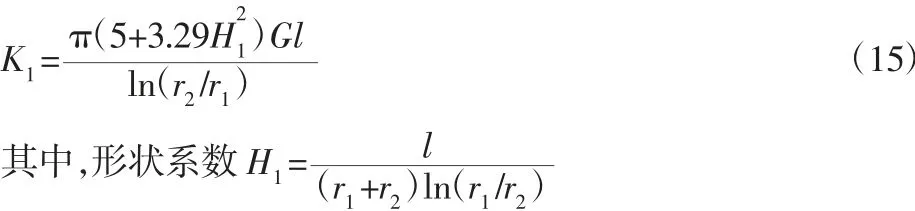
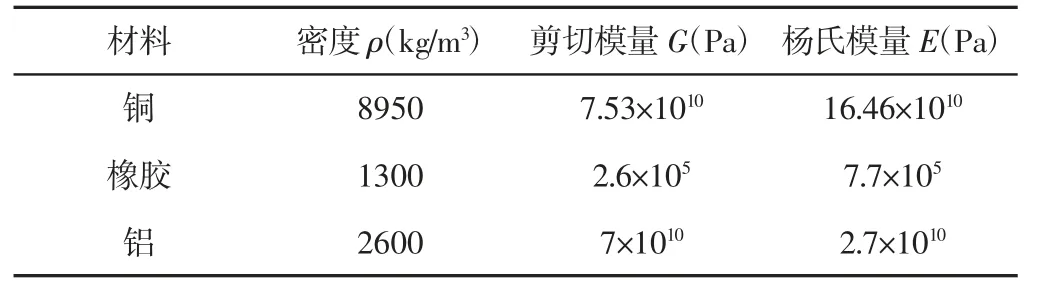
表1 材料参数Tab.1 Material Parameters

3.1 算法收敛性

第一带隙和第二带隙的起止频率随弹簧振子数N 的变化规律，如图4 所示。其中，将第一级橡胶和第二级橡胶等效为相同个数的弹簧振子（即N1=N2）的串联系统计算。由图可知，第一带隙的起止频率范围随着弹簧振子数N 的增加逐渐降低，当N=6（N1=N2=3）时已经基本趋于稳定；第二带隙的起止频率随着弹簧振子数N 增加到10（N1=N2=5）时基本保持不变。因此，该算法具有较好的收敛性。

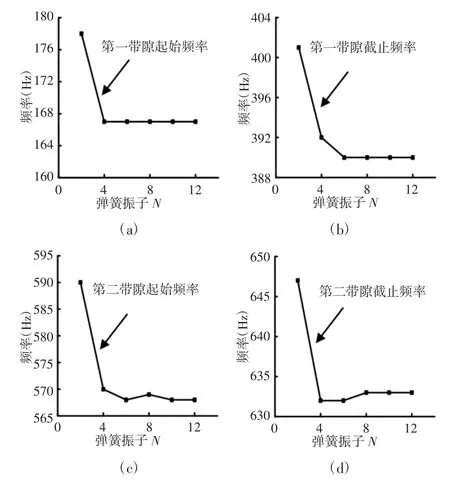
图4 带隙的起止频率随弹簧振子数N 的变化Fig.4 The Changes of Start-Stop Frequency of Band Gaps with the Number of Spring-Mass N

3.2 振动特性计算

采用考虑离散弹簧质量的传递矩阵法，将第一级和第二级橡胶分别等效为5 个相同的弹簧振子串联系统，即将两级局域共振子结构等效为N=10 个弹簧振子串联系统，根据式（14）可以计算出两级局域共振子欧拉梁的能带结构，如图5 所示。图5 中所示的实线为考虑离散弹簧质量的传递矩阵法的计算结果，其第一带隙频率范围为（163～390）Hz，第二带隙频率范围为（570～632）Hz；其中所示的虚线为传统传递矩阵法的计算结果，其带隙范围为（178～401）Hz 和（590～647）Hz。为了验证算法的准确性，下面计算两级局域共振子结构的传输特性曲线。

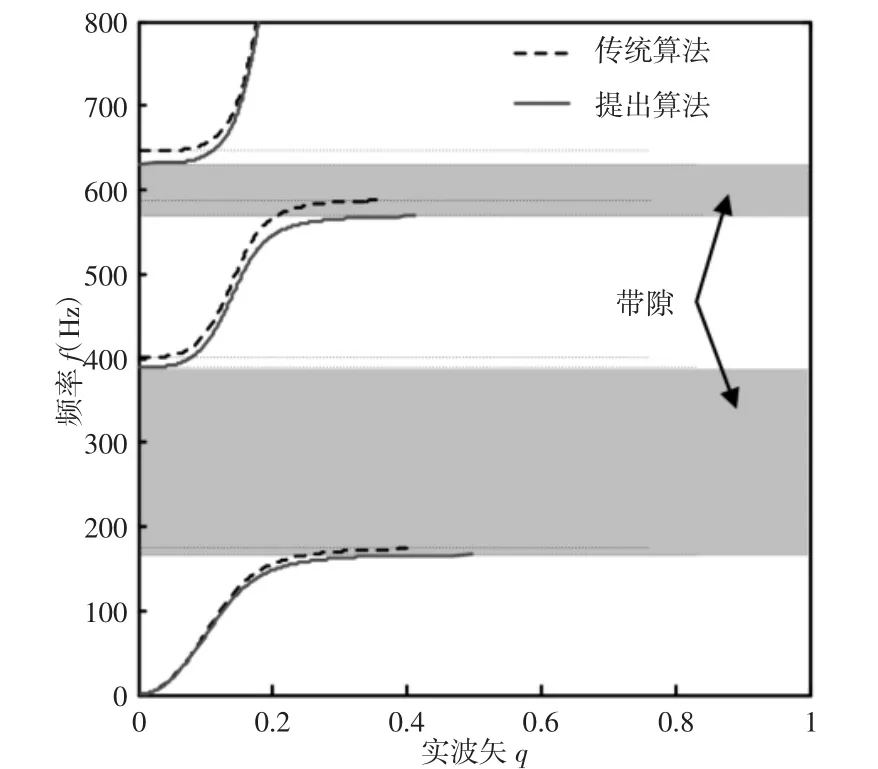
图5 采用不同算法计算的两级局域共振子欧拉梁的能带结构Fig.5 Complex Band Structure of the Two-Stage Local Resonators Euler Beam Calculated by Different Methods

首先在patran 中建立8 个两级局域共振子周期结构，在该结构的一端施加垂直于轴向的径向加速度激励，使得弯曲振动沿着结构的周期方向传播，在另一端拾取加速度响应，输出响应和输入响应的频谱相比，即可得到传输特性曲线，如图6 所示。可以看到，其获得的带隙频率范围为（166～390）Hz，（563～621）Hz。传输特性曲线具有平均约20dB 的振动衰减量。

图6 两级局域共振子欧拉梁的传输特性曲线Fig.6 Transmission Characteristic Curve of Two-Stage Local Resonators Euler Beam

将传统传递矩阵法和考虑离散弹簧质量的传递矩阵法的计算结果与有限元法结果相比发现，考虑离散弹簧质量的传递矩阵法比传统传递矩阵法更好地吻合有限元的结果。但是在频率较高的第二带隙起止频率处，提出算法与有限元法的结果之间存在一定的偏差，这主要是由于提出算法基于连续质量离散化的思想在高频处与有限元思想存在差异造成的。

为了分析附加相同质量时，单级局域共振子结构和两级局域共振子结构的振动带隙特性，选择单级局域共振子的结构参数为r0=0.007m，r1=0.01m，r2=0.015m，r3=0.0256m，梁的参数设置与前文保持一致，单级局域共振子的材料也选择铜。获得的能带结构，如图7 所示。其中虚线代表相同附加质量的单级结构的带隙，频率范围为：（185～475）Hz，带宽为290Hz；实线代表上文所述的两级结构的带隙，其第一和第二带隙的总带宽为285Hz。由此可知，附加相同的质量时，两级结构具有比单级结构更低的带隙起始频率和覆盖频率范围更高的第二带隙，且总带宽基本相同。

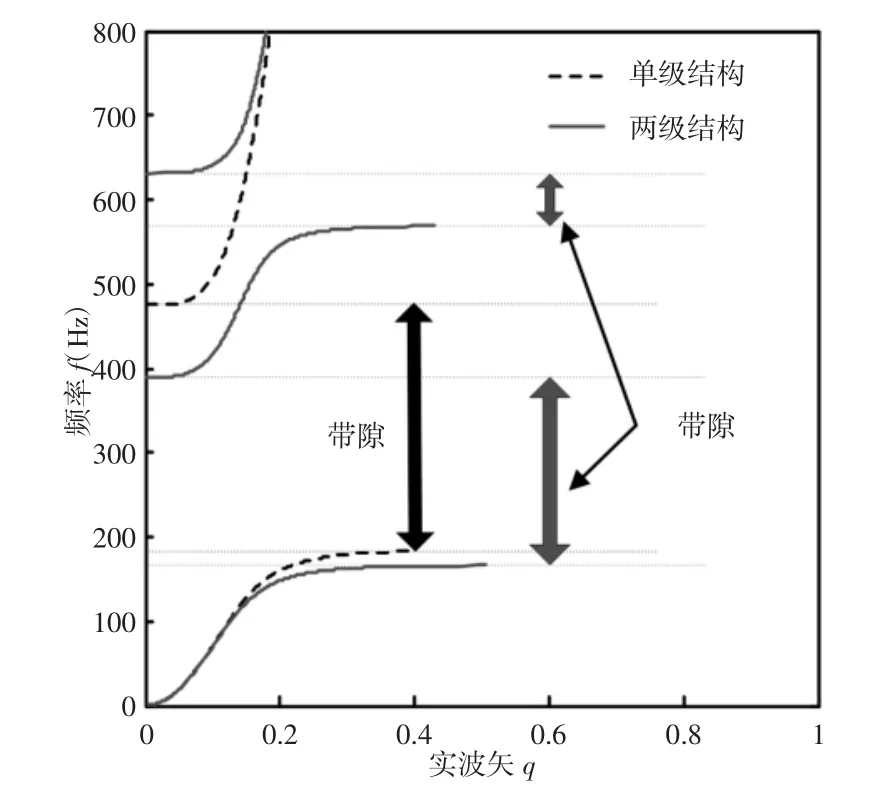
图7 附加相同质量时单级结构和两级结构的振动带隙特性Fig.7 Vibration Band Gap Characteristics of One-Stage Structure and Two-Stage Structure with the Same Mass Added

4 材料密度对带隙特性的影响

梁和散射体的密度对带隙的影响，如图8～图10 所示。由图8 可知，第一和第二带隙的截止频率受梁的密度的影响比较大。随着梁的密度逐渐升高，带隙的截止频率迅速降低，而起始频率基本保持不变。这是因为起始频率主要由两级局域共振子的谐振频率决定，与梁的密度无关。每一级散射体的密度对带隙都有着一定的影响，如图9～图10 所示。随着散射体密度的升高，散射体的质量增大，导致散射体谐振频率降低，因此带隙频率随着下降。此外，由图9 还可以发现，当着重关注于低频第一带隙时，随着第一级散射体密度的减小，第一带隙的起止频率基本保持不变，这样第一级散射体可以采用更小密度的材料来减小附加的局域共振子质量。