一种基于精英反向和纵横交叉的鲸鱼优化算法
2020-10-21赵露露
刘 琨,赵露露,王 辉
(河南理工大学 计算机科学与技术学院,河南 焦作 454000)
1 引 言
全局优化问题广泛存在于数学、经济、系统优化和工程实践等领域中,对于具有高维、非线性、多极值、目标函数不可导等特点的复杂全局优化问题,传统优化算法很难获得理想的优化效果,而群智能优化算法为求解此类优化问题提供了有效的解决方案.近年来,许多群智能优化算法如粒子群算法[1],蚁狮优化算法[2],蜻蜓算法[3],蝗虫优化算法[4],灰狼优化算法[5],正弦余弦算法[6]等相继被提出,并用于解决复杂全局优化问题.
鲸鱼优化算法(Whale Optimization Algorithm,WOA)是Mirjalili等人在2016年提出的一种新型智能优化算法[7].该算法具有原理简单、结构灵活、易于理解且便于实现等优点,但其同样存在收敛速度慢、易陷入局部最优和收敛精度低的问题.为此,许多学者针对鲸鱼优化算法的不足做了相应的改进.例如,Zhou等人[8]将Levy飞行引入鲸鱼优化算法中以增加种群多样性,从而提高算法跳出局部最优解的能力;Kaur等人[9]将混沌理论引入鲸鱼优化算法的优化过程中,以此提升算法的收敛速度;Sun等人[10]提出一种改进的鲸鱼优化算法用于解决大规模优化问题,该算法利用非线性收敛因子来协调算法的探索和开发能力,采用二次插值法对最优解进行变异并结合Levy飞行策略避免算法陷入局部最优;涂春梅等人[11]提出一种混沌反馈自适应鲸鱼优化算法,将混沌初始策略用于初始化种群,增加了反馈阶段来提高算法的全局探索能力,同时引入自适应惯性权重帮助算法跳出局部最优,实验证明该算法具有更好的收敛精度和稳定性;褚鼎立等人[12]提出一种基于自适应权重和模拟退火的鲸鱼优化算法,通过改进的自适应权重加快局部收敛速度,并结合模拟退火策略来提升算法全局寻优能力,从而有效提高了算法的收敛精度和优化性能.
上述改进策略在一定程度上改善了WOA算法的性能,然而对于复杂或规模较大的函数优化问题,算法的收敛速度和精度仍有提升的空间.因此,本文提出一种基于精英反向和纵横交叉的鲸鱼优化算法(Elite Opposition-Based and Crisscross Optimization for Whale Optimization Algorithm,ECWOA).该算法首先通过精英反向学习策略初始化种群,提高初始解的质量,为算法快速收敛奠定基础;其次,引入非线性收敛因子平衡算法的全局探索能力和局部开发能力,从而改善算法的收敛速度和求解精度;最后,利用纵横交叉策略对种群个体和全局最优解进行修正,在保持种群多样性的同时,避免算法陷入局部最优.通过8个测试函数验证ECWOA算法的性能,实验结果表明该算法在函数优化问题上表现优异,具有较好的收敛精度和收敛速度,并能有效防止算法陷入局部最优.
2 鲸鱼优化算法
WOA算法通过模拟座头鲸的捕食行为实现对复杂优化问题的寻优,将待求解问题的解空间类比于鲸鱼种群,鲸鱼个体代表待求解问题的可行解,最优个体为最优解,其他个体通过收缩包围、发泡网攻击和随机搜索三种方式更新自身位置向最优个体趋近,经过多次迭代更新后求得最优解.
2.1 收缩包围
令鲸鱼种群规模为N,鲸鱼种群S={s1,s2,…,sN},由于WOA算法初始化鲸鱼种群是无先验经验的,所以假设当前最优个体为目标猎物,迭代过程中鲸鱼种群中的其他个体均向猎物靠近,位置更新公式如下:
si(k+1)=sbest(k)-A|Csbest(k)-si(k)|
(1)
A=2ar1-a
(2)
C=2r2
(3)
式中,si(k)为第i个鲸鱼个体的位置,k为当前迭代次数;sbest(k)为当前最优鲸鱼个体的位置;A和C为系数变量;r1和r2为区间[0,1]上的随机数;a=2-2k/Kmax为收敛因子,Kmax为最大迭代次数.
2.2 发泡网攻击
发泡网攻击是座头鲸通过螺旋向上的方式逐步缩小包围进行捕食的过程.该过程中的收缩包围和螺旋更新是一种同步行为,当|A|<1时,个体以50%的概率作为阈值来确定更新方式是螺旋更新或收缩包围,更新公式如下:
(4)
式中,b为对数螺旋形状常数;l为区间[-1,1]上的随机数;p为[0,1]上的随机数.
2.3 随机搜索
鲸鱼在捕猎过程中除了可以进行发泡网攻击之外,还可以通过随机游动来搜寻猎物.当|A|≥1时,鲸鱼根据彼此的位置对猎物进行随机搜索,使算法具有一定的全局搜索能力,位置更新公式如下:
si(k+1)=srand(k)-A|Csrand(k)-si(k)|
(5)
式中,srand(k)为当前群体中随机选择的鲸鱼个体.
3 基于精英反向和纵横交叉的鲸鱼优化算法
为了解决WOA算法收敛速度慢,易陷入局部最优等问题,本文通过精英反向学习、非线性收敛因子和纵横交叉三种策略对WOA算法进行改进,提出一种基于精英反向和纵横交叉的鲸鱼优化算法(ECWOA),下面详细介绍三种改进策略.
3.1 精英反向学习策略
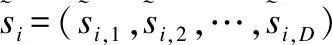
(6)

(7)
式中,rand(lbj,ubj)为区间[lbj,ubj]上的随机值.
精英反向学习策略初始化种群的基本步骤如下:
1)随机初始化种群S,选前N/2个适应度较优的个体组成精英种群E.
2)求出精英种群E的反向种群OE.
3)合并种群S和OE得到新种群{S∪OE},从中选择N个适应度较优的个体组成初始种群.
3.2 非线性收敛因子
在标准WOA算法中,系数A是影响全局探索和局部开发能力平衡的关键因素,当系数|A|≥1时,种群扩大搜索区域,以搜索到更好的候选解,即算法进行全局探索;当系数|A|<1时,种群将缩小搜索范围,在局部区域进行精细搜索,即算法进行局部开发.而从式(2)中可以看出,系数A的值是由线性递减的收敛因子a决定的,无法准确地反映复杂的非线性搜索过程.因此,本文引入逆不完全Γ函数来更新收敛因子a,其具体表达式为:
(8)
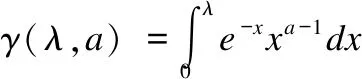
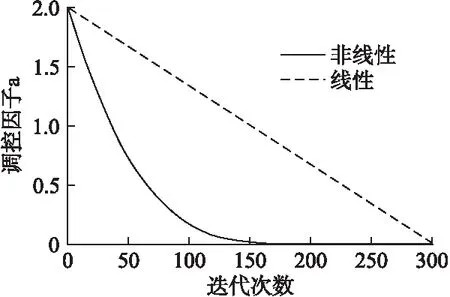
图1 非线性收敛因子的递减曲线Fig.1 Nonlinear convergence factor decline curve
图1为amin=0,amax=2,λ=0.01时,非线性收敛因子a的递减曲线.从可以看出,相比于线性递减的收敛因子a,逆不完全Γ函数具有的优良特性使得非线性收敛因子a在算法迭代初期接近线性下降,有利于算法进行全局探索;而在算法迭代后期,a开始呈现指数形式下降,有利于算法进行局部开发.非线性收敛因子能够更好的协调算法的全局探索和局部能力,进一步提升算法的寻优性能.
3.3 纵横交叉策略
由于种群中的鲸鱼个体在迭代过程中向最优个体聚集,若存在一个局部最优解,随着迭代次数的增加,鲸鱼个体聚集在局部最优解周围,易导致种群多样性下降.为了避免算法陷入局部最优,防止“早熟”现象的发生,本文引入纵横交叉策略[14]对种群个体和全局最优解进行修正,利用横向交叉对种群进行交叉搜索以减少搜索盲点,通过纵向交叉对最优解进行交叉运算,在增加种群多样性的同时能够降低算法陷入局部最优的概率.纵横交叉策略产生的候选解与其父代进行竞争获得的占优解会呈链式反应迅速传播至整个种群,从而提升算法求解精度并加快收敛速度.
3.3.1 横向交叉

(9)
(10)
3.3.2 纵向交叉
WOA算法在迭代后期易陷入局部最优,往往是由于种群更新过程中某些个体的某一维陷入局部最优而造成的.纵向交叉能够以概率Pv对全局最优解Fbest的两个不同维的进行交叉运算,使同一个体不同维之间相互学习,有利于陷入局部最优的维度跳出局部最优.并且纵向交叉每次只对其中一维进行更新既能够使陷入局部最优的维度跳出局部最优,而又尽可能不破坏另一正常维度包含的信息.假设对Fbest的第d1维和第d2维进行纵向交叉,通过下式产生子代个体:
(11)

3.4 ECWOA算法
结合标准鲸鱼优化算法以及上述改进策略,本文提出的ECWOA算法的伪代码如下:
1.设置种群规模N,维度D,最大迭代次数Kmax,横向交叉概率Ph,纵向交叉概率Pv等,令当前迭代次数k=1
2.利用精英反向学习策略初始化种群{si,i=1,2,…,N}
3.计算种群个体适应度{f(si),i=1,2,…,N},记录当前最优个体sbest
4.While(k 5.Fort=1toN 6. 根据式(8)、式(2)和式(3)分别更新收敛因子a、参数 A和C,更新概率p∈[0,1]和随机数l∈[-1,1] 7.If(p<0.5) 8.If(|A|<1) 9. 进行收缩包围,根据式(1)更新个体位置; 10.elseif(|A|≥1) 11. 进行随机搜索,根据式(5)更新个体位置; 12.Endif 13.elseif(p≥0.5) 14. 进行螺旋更新,根据式(4)更新个体位置; 15.Endif 16.Endfor //横向交叉 17. rand1=randperm(N)//产生1到N的随机整数序列 18.Fori=1toN/2 19. 生成随机数p1∈[0,1] 20.If(p1 21.Ford=1toD 24.Endfor 27.Endif 28.Endfor //纵向交叉 29. 计算种群适应度,更新sbest并对sbest进行归一化处理 30. rand2=randperm(D)//产生1到D的随机整数序列 31.For j=1 to D/2 32. 生成随机数p2∈[0,1] 33.If (p2 (2j) 35.Endif 36.Endfor 39.k=k+1 40.Endwhile 41.输出最优个体sbest及其适应度f(sbest). ECWOA算法主要由精英反向学习、非线性收敛因子、鲸鱼位置更新以及纵横交叉策略组成.当种群规模为N,搜索空间维度为D,最大迭代次数为Kmax时,本文算法时间复杂度分析如下:精英反向学习初始化种群的时间复杂度为O(ND);迭代过程中,非线性收敛因子是在原收敛因子的基础上进行改进,并没有增加额外的时间复杂度,时间复杂度仍为O(KmaxN);鲸鱼个体位置更新的时间复杂度为O(KmaxND);纵横交叉策略的时间复杂度为O(KmaxND/2+KmaxD/2)=O(KmaxND),其它各步计算规模较小,略去不计.因此,ECWOA算法的整体时间复杂度为O(KmaxND),与标准鲸鱼优化算法的时间复杂度保持一致. 为了验证ECWOA算法的优化性能,本文在8个测试函数上进行仿真实验,并与粒子群算法[1](Particle Swarm Optimization,PSO)、灰狼优化算法[5](Grey Wolf Optimization Algorithm,GWO)、基本鲸鱼优化算法(WOA)、基于精英反向的花授粉算法[13](Elite Opposition-based Flower Pollination Algorithm,EOFPA)、纵横交叉算法[14](Crisscross Optimization Algorithm,CSO)以及改进的鲸鱼优化算法[15](Modified Whale Optimization Algorithm,MWOA)进行比较.采用最优值Best、最差值Worst、均值Mean和标准差Std作为评价指标,其中最优值和最差值反映解的质量,均值反映算法所能达到的精度,标准差反映算法的鲁棒性和稳定性.本文仿真实验基于Windows 7操作系统,3.2GHz主频及4GB内存,编程采用MATLAB R2014a软件. 表1 测试函数Table 1 Test functions 在进行仿真实验时,为了使实验结果更加公正和客观,将所有算法的规模均设置为30,最大迭代次数设置为300.PSO、GWO、CSO、EOFPA和MWOA算法的其余参数设置同其相应的参考文献一致.ECWOA算法的参数如下:收敛因子a最小值amin=0,最大值amax=2,随机变量λ=0.01,横向交叉概率Ph=1,纵向交叉概率Pv=0.6,对数螺旋形状常数b=1;标准WOA算法参数设置与ECWOA算法相同. 本文选取8个具有不同特点的测试函数进行仿真实验,其名称及特性见表1,其中f1~f3为单峰函数,f4~f6为不定维多峰函数,f7和f8为固定维多峰函数. 为了验证ECWOA算法在不同维度下的性能,设置函数f1~f6维度分别为30、50和100,将ECWOA与WOA算法在6个测试函数上独立运行50次,仿真结果如表2所示.从中可以看出,ECWOA在不同维度下的收敛精度均优于WOA.尤其是对于多峰函数f4和f5,无论低维还是高维,ECWOA均可以收敛到其理论最优值0,而WOA的收敛精度随着维度增加有所下降.另外,ECWOA在各个函数上的标准差非常小,对于多峰函数f4、f5和f6,在不同维度下所求得的标准差均为0,说明ECWOA具有较强的鲁棒性和稳定性.由此可知,随着函数维度的增加,待求解函数的复杂程度也随之增加,从而导致ECWOA的寻优精度和稳定性有所下降,但ECOWA的寻优性能还是优于标准WOA. 表2 WOA、ECWOA算法在不同维度下的实验结果Table 2 Experimental results of WOA and ECWOA algorithm in different dimensions 表3为PSO、GWO、WOA、CSO、EOFPA、MWOA和ECWOA算法在8个测试函数(其中f1~f6的维度D=30)上独立运行50次得到的实验结果.从表3中可以看出,对于单峰函数f1~f3,ECWOA寻优的均值和标准差与其他算法相比高出多个数量级,说明ECWOA的求解精度和稳定性相对较好.特别是对于极难求得最优解的函数f2,ECWOA不仅可以收敛到其理论最优值,而且在各项指标上的表现均优于其他算法.针对多峰函数f4和f5,CSO、EOFPA、MWOA以及ECWOA均可以搜索到函数的理论最优值且寻优的标准差均为0,PSO寻优效果最差.对于多峰函数f6,该函数全局最优点周围存在无数次优点为算法的寻优过程增加了难度,虽然所有算法均无法搜索到其理论最优值,但ECWOA和EOFPA寻优的均值、方差和最优值优于其他算法.函数f7为固定维度为2的多峰函数,ECWOA和EOFPA寻优得到的均值相同,但在标准差指标上,ECWOA获得最优值,说明ECWOA具有更好的稳定性.对于固定维度为6的多峰函数f8,ECWOA可以收敛到其理论最优值,且寻优的最差值、均值和标准差均优于其他算法. 表3 算法对比Table 3 Comparison of algorithms 图2 函数收敛曲线Fig.2 Function convergence curve 图2为不同算法在测试函数上的收敛曲线,从图2中可以看出,对于单峰函数f1和f3,CSO、EOFPA以及MWOA虽未陷入局部最优,但因收敛速度过于缓慢使得算法无法获得更好的求解精度,而ECWOA通过非线性收敛因子加快了算法的收敛速度,从而有效提高了算法的求解精度.求解函数f2和f8时,其他算法均过早的收敛到局部最优解,而ECWOA通过非线性收敛因子合理控制收敛速度以及纵横交叉策略提高了算法跳出局部最优解的能力,最终收敛到理论最优值.对于多峰函数f4和f5,CSO、EOFPA、MWOA和ECWOA均能够收敛到其理论最优值,但ECWOA迭代不到75次就能够收敛到理论最优值,收敛速度明显优于其他算法.在函数f6和f7的优化过程中,所有算法在迭代后期均陷入局部最优,但在迭代结束时,ECWOA和EOFPA获得了更好的求解精度. 综上所述,ECWOA算法在单峰、多峰函数上的寻优性能均优于PSO、GWO、WOA、CSO、EOFPA和MWOA算法.这主要得益于高质量的初始种群、非线性动态变化的收敛因子以及纵横交叉策略,通过这些改进策略ECWOA算法能有效平衡全局探索和局部开发能力,避免算法陷入局部最优,使得算法在收敛速度、求解精度和稳定性方面均表现出较好的性能. 为进一步提高鲸鱼优化算法的寻优能力,本文提出了一种基于精英反向学习和纵横交叉的鲸鱼优化算法,该算法利用精英反向学习生成初始种群以维持初始群体的多样性;设计了一种基于逆不完全Γ函数的收敛因子使其随迭代次数增加非线性动态变化,以平衡算法的全局探索和开局部发能力;引入纵横交叉策略使个体信息在种群中呈链式反应迅速传播交流,从而避免算法陷入局部最优.通过对8个测试函数进行仿真实验表明,与PSO、GWO、WOA、CSO、EOFPA和MWOA算法相比,ECWOA算法具有更好的收敛速度、求解精度和稳定性.后续工作将从理论上对ECWOA算法的收敛性进行分析,并考虑将该算法应用于实际的优化问题中.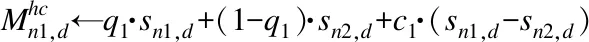
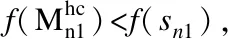
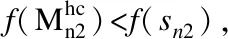

3.5 改进算法时间复杂度分析
4 实 验
4.1 实验设置

4.2 参数设置及测试函数
4.3 维度变化分析

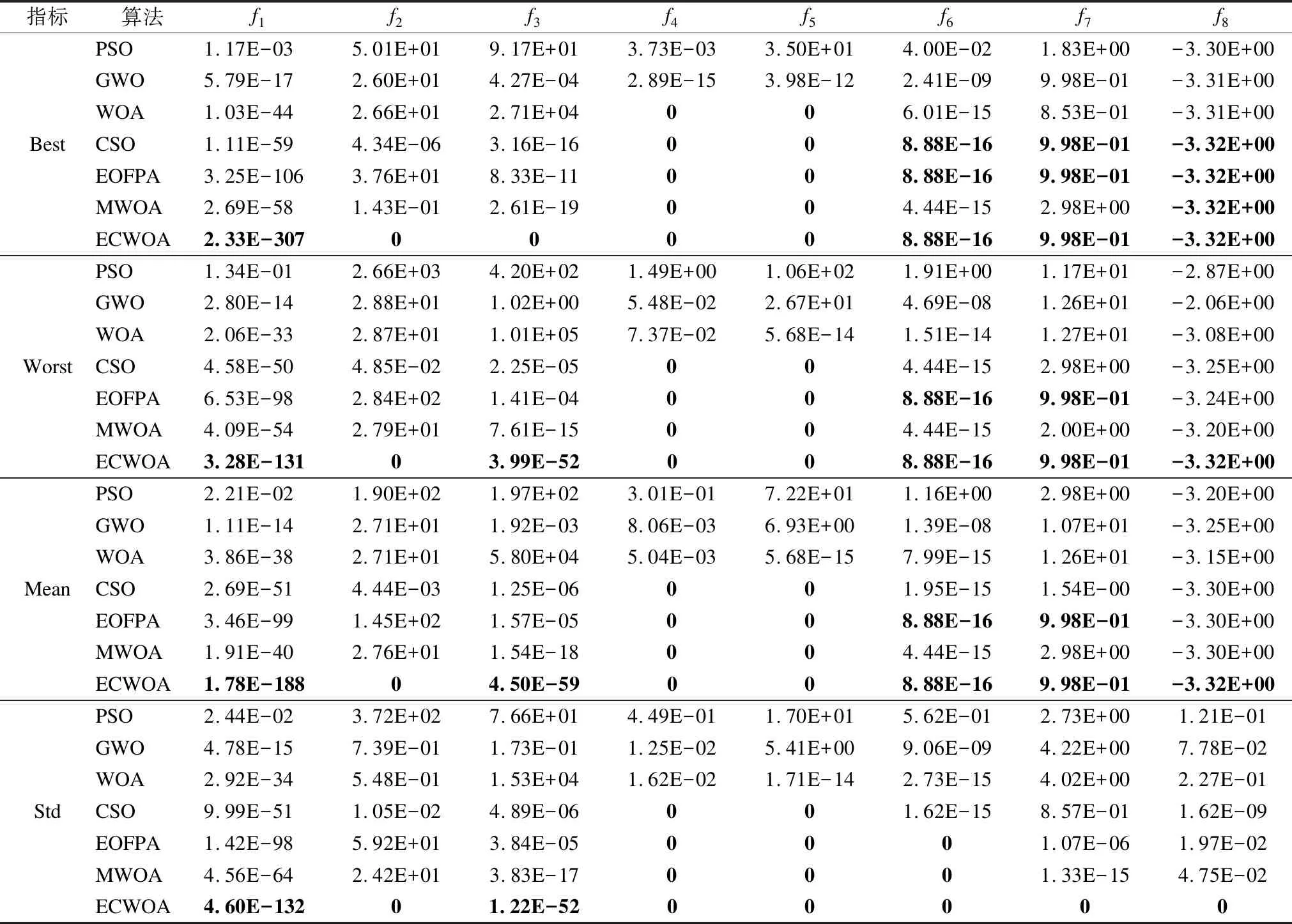
4.4 算法对比分析

5 结束语
