基于均衡接近度增强时间的兴趣点推荐模型
2020-10-21陈江美张岐山张文德
陈江美,张岐山,张文德,何 珑
1(福州大学 经济与管理学院,福州 350108) 2(福州大学 信息管理研究所,福州 350108) 3(福州大学 网络与信息化建设办公室,福州 350108)
1 引 言
随着智能终端设备的普及和定位技术的发展,人们更加容易地获得实时的位置信息,基于位置的社交网络(location-based social network,LBSN)应运而生[1].在LBSN中,用户根据个人喜好选择兴趣相投的兴趣点(point-of-interest,POI),并以“签到”的方式与朋友分享他们感兴趣的兴趣点.兴趣点推荐增强了用户的个性化体验,如何帮助用户从大量的兴趣点中挖掘出他们喜欢的地点不断引起学术界的关注,成为了推荐领域研究的热点.
目前,大多数的研究[2-4]主要利用用户的历史签到记录并融合相关的上下文信息(如地理信息、社交信息等)进行推荐.为了进一步了解用户的移动行为,少数学者将时间融入兴趣点推荐领域中,但推荐精度有待提高,同时现存的研究仍面临一些挑战.首先,LBSN中的每个用户仅签到有限个兴趣点,用户签到矩阵极其稀疏,若根据时间划分用户偏好矩阵,会造成更严重的数据稀疏问题.其次,大多数用户在一天中的不同时间有不同的签到偏好,例如中午去餐馆,晚上去商场,如何更好地建模时间影响是一大难点.最后,LBSN中存在大量的异构信息,这些信息对兴趣点推荐的性能发挥着不同程度的影响,如何有效融合这些信息值得关注.
针对以上问题,本文提出了一种基于均衡接近度增强时间的兴趣点推荐模型(GB-TSP).首先,本文将时间因素融入基于用户的协同过滤算法中,用均衡接近度方法度量时间相似度,获得时间影响模型.其次,将时间流行度与地理影响结合,获得空间影响模型.综合考虑上述时空的影响,为每个用户学习到一组兴趣点并将其填充进矩阵,有效地缓解了数据稀疏性.最后,考虑时间影响,将填充后的矩阵通过矩阵分解得到最终的偏好预测矩阵,进而完成推荐.具体地,本文的创新主要体现在以下三个方面:
1)考虑合并时间的签到矩阵极其稀疏,用均衡接近度的方法度量时间相似度,进而平滑用户间的相似度,构建融合均衡接近度的时间影响模型.
2)采用矩阵填充的方式,通过增加签到数据记录来有效缓解数据稀疏的影响.再通过矩阵分解获得用户偏好预测矩阵,实现实时推荐.
3)有效地建模时间因素、地理位置因素和兴趣点的时间流行度的影响,并将时间因素有效地融入基于用户的协同过滤算法和矩阵分解算法中.
2 相关工作
2.1 兴趣点推荐的相关研究现状
兴趣点推荐是一种基于情景信息的感知推荐,主要通过用户签到数据并融合相关情景信息来完成推荐工作.目前,基于地理位置的兴趣点推荐研究较为成熟.相关学者提出一些经典的模型,如USG[5]、iGSLR[6]、GeoMF[7]等.USG模型将地理和社交信息融入基于用户的协同过滤框架中,并采用幂律分布建模地理因素,但人为地赋予用户统一的空间先验分布无法满足用户个性化的偏好.iGSLR模型采用核密度估计分布来建模地理影响,一定程度上满足了用户个性化的需求.但由于采用简单的线性融合方法建模用户的签到行为,导致推荐效果不佳.据此,文献[7]提出将地理信息嵌入加权矩阵分解算法中,充分考虑隐式信息的影响.Zhang等人[8]将地理、社交和兴趣点分类信息分别建模,并采用混合算法融合不同的情景信息.上述模型的性能虽有所提高,但由于遭受严重的数据稀疏影响,推荐效果一般.为了缓解稀疏问题,Li等人[9]提出“两步走”的框架,利用地理和社交信息为每个用户学习一组待填充兴趣点,通过矩阵填充的方式缓解稀疏影响.王峥等人[10]通过社交信息度量用户兴趣相似度,结合通过非负矩阵分解算法获得的熟悉度预测用户相似度,使其在稀疏数据情况下计算出更精确的相似度.上述模型有效地缓解了稀疏问题,但由于考虑的情景因素有限,造成对兴趣点属性的挖掘不够全面.基于此,相关学者[11,12]通过纳入流行度信息来改善推荐性能.Yuan等人[11]利用流行度信息度量兴趣点被签到的先验概率,并将其与基于幂律分布的地理模型结合.吴燕等人[12]综合考虑时间、地理和兴趣点流行度的影响,利用最近邻候选兴趣点的方法刻画用户的地理偏好,将其与兴趣点流行度相结合进行推荐.同时,用户的偏好是动态变化的,为了更好地建模用户的移动行为模式,时间信息被充分挖掘.Gao等人[13]考虑时间非统一性和连续性的影响,将其融入矩阵分解模型中,实现实时推荐的效果.此模型有效利用时间建模,但考虑因素单一,准确率极低.在此基础上,文献[14]考虑时间、地理和社交信息的影响,并将各情景信息建立在统一的框架中.文献[11]考虑地理位置因素和兴趣点流行度,并嵌入时间信息.这些模型有效地考虑用户偏好的动态变化问题,但由于将时间划分造成更严重的数据稀疏问题,使得推荐的准确率不佳.
综上,本文综合考虑数据稀疏和用户兴趣动态变化的问题,提出了一种基于均衡接近度增强时间的兴趣点推荐模型.采用矩阵填充的方式缓解稀疏问题,并将时间信息与地理位置以及兴趣点流行度结合,实现实时推荐的效果.
2.2 均衡接近度方法
均衡接近度方法由张岐山教授[15]提出,由传统的灰关联系数发展而来的一种计算复杂贫信息系统的两向量之间的接近度的方法.
定义 1.(灰关联度) 设X为灰关联因子集,X0={x0(k)|k∈K}为参考列,Xi={xi(k)|k∈K}为比较列,i={1,2,3,…,m},K={1,2,3,…,n}:
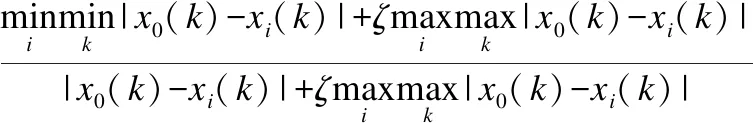
(1)
(2)
其中,γ(X0,Xi)为第i个比较列的灰关联度;ζ为分辨系数.
定义 2.(均衡度) 设第i个比较列的关联系数列用Ri表示:Ri={γ(x0(k),xi(k)),k∈K},i={1,2,3,…,m},K={1,2,3,…,n}:
(3)
(4)
其中,B(Ri)为第i个比较列的均衡度;lnn为最大熵.
定义 3.(均衡接近度) 设B(X0,Xi)为参考列X0和比较列Xi的均衡接近度:
B(X0,Xi)=B(Ri)×γ(X0,Xi)
(5)
均衡接近度方法改进了邓聚龙教授[16]提出的灰关联系数的方法,能有效克服灰关联系数存在的信息损失和局部点关联倾向的不足.文献[17]将均衡接近度融入到各类算法中,用来预测数据间的相似性程度,减弱局部强关联性造成的影响.文献[18]将灰色预测模型引入到推荐系统,用来缓解数据稀疏性和相关性等问题.基于此,考虑根据时间段划分签到矩阵会使得数据更加稀疏,本文提出利用均衡接近度来计算每个时间段间的相似度,将其作为平滑因子,有效改进时间影响模型,提高推荐准确率.
3 融合时空的矩阵填充模型
对融合时空影响的矩阵填充建模是本文的第一阶段,主要任务是通过建立时间影响模型和空间影响模型,为每个用户学习出一组可能签到的兴趣点和时间,将其填充进矩阵,完成矩阵填充.
3.1 基于均衡接近度的时间影响
本文将时间按小时为单位分为24个时间段,为了获得用户间的时间行为相似性,利用余弦相似度来计算两用户的相似度,如下:
(6)
其中,ru,t,l和rv,t,l分别表示用户u和v在t时刻对兴趣点l的签到次数.
采用式(6)计算用户相似度存在两个问题:一是将时间划分导致数据更加稀疏;二是用户在某些时间段无签到行为会造成无意义的相似度计算.因此,本文采用时间平滑技术,修正原始的签到次数.
给定用户u,设Ru,t=(ru,t,l1,ru,t,l2,…,ru,t,ln)表示用户u在时间段t内的签到向量.考虑均衡接近度能有效处理复杂贫信息系统的数据,本文用式(5)的均衡接近度度量时间段ti和tj的相似度,如下:
(7)
取所有用户的相似度的平均值作为两时间段的相似度,如下:
(8)
利用上述的值去平滑签到次数ru,t,l,如下:
(9)
将式(9)代入式(6),得到平滑后的用户相似度:
(10)
最终,本文将通过平滑技术得到用户u在时间段t对兴趣点l的签到得分定义如下:
(11)
3.2 融合时间流行度的空间影响
本文考虑用户更倾向于签到距离自身近的兴趣点,采用文献[19]提出的幂律分布模型对地理建模,因此用户在距离d-km远的位置签到的概率为:
PrG(d)=a·db
(12)
其中,a和b是幂律分布的参数.
设用户u的历史签到记录为Lu,li∈Lu.本文将用户u对未签到兴趣点lj的访问概率建模如下:
(13)
最终,根据贝叶斯规则,得到用户u对未签到兴趣点l在空间上的签到得分,如下:
(14)
其中,∝表示正向于;P(l)表示兴趣点l被所有用户签到的先验概率.
在此基础上,本文考虑用户对兴趣点的签到概率除了与空间距离相关,还与兴趣点在某时间段的流行度相关,即兴趣点的受欢迎程度会随着时间不断变化.为了验证这一点,图1绘制了从Foursquare数据集中选取两个兴趣点的时间流行度的情况.其中,兴趣点l在时间段t内的流行度为t时间段上所有用户对兴趣点l的签到次数与兴趣点l在所有时间段上被签到总次数的比值.从图1明显看出,每个兴趣点的流行度随时间变化很大,所以考虑将时间流行度纳入模型极其重要.
因此,本文将时间流行度融入空间模型,如下:
(15)
其中,|Rl|表示兴趣点l被签到的次数;|Rl,t|表示兴趣点l在时间段t内的被签到次数;式(15)第一项表示兴趣点l在时间段t内被签到的概率,即兴趣点l的时间流行度.第二项表示不考虑时间因素的兴趣点l的被签到的先验概率;参数α作为时间流行度的权重系数.
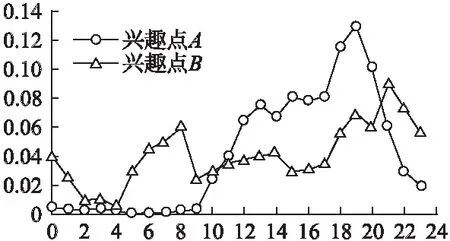
图1 兴趣点的时间流行度分布Fig.1 Distribution of POI′time popularity
因此,本文将兴趣点的时间流行度融入空间影响模型,利用式(15)获得的Pt(l)调整式(14)的p(l),得到用户u在时间段t对兴趣点l的签到得分,如下:
(16)
3.3 统一框架
在3.1和3.2节中,本文分别建立了时间影响和空间影响模型,通过考虑时间、空间和流行度分别对其建模.本节综合考虑上述两种模型,获得最终的矩阵填充模型,将得分最高的top-n个兴趣点和相应的时间填充进原始矩阵.考虑两种模型的度量方法有差异,整合前先采用min-max归一化的方法对两个分数进行处理,如下:
(17)
(18)
最终,得到用户对兴趣点的综合分数如下:
(19)
根据上述结果,将分数最高的top-n个兴趣点填充进原始矩阵,完成矩阵填充的过程.
4 融合时间的矩阵分解模型
矩阵分解技术在推荐算法中被广泛使用,对通过矩阵填充后的新矩阵进行矩阵分解是本文的第二阶段.在文献[13]提出的LRT模型的基础上,考虑受到数据稀疏问题的影响,本文对时间接近度的计算用均衡接近度方法改进,并采用加权矩阵分解算法将时间因素融入到模型中.
4.1 时间非统一性

(20)
考虑时间的非统一性,通过优化以下的损失函数来获得特征偏好,如下:
(21)
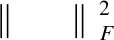
同时,本文通过填充矩阵得到的新矩阵Pt包含三类兴趣点,分别是用户已签到和未签到的兴趣点,以及待填充的兴趣点.并采用加权矩阵分解算法得到偏好矩阵Pt的元素pu,t,j和权重矩阵Wt的元素wu,t,l,如下:
(22)
(23)
其中,θ表示用户u以θ的概率签到矩阵填充纳入的兴趣点;η是调整参数.
4.2 时间连续性
时间连续性指用户在连续时间状态具有更相似的签到偏好.为了建模此属性,本文利用均衡接近度计算时间接近度,并将此融入模型,得到损失函数如下:
(24)

ζu(t,t-1)=simti,tj
(25)
其中,simti,tj表示用均衡接近度计算的两个时间段间的接近度.
4.3 统一模型
通过4.1和4.2节的分析,本节综合考虑时间非统一性和时间连续性的影响.将式(21)与式(24)综合,最终通过解决以下优化问题来获得用户的签到偏好,如下:
(26)
其中,λt表示用来调整时间正则化的参数.
本文采用交替最小二乘(ALS)法优化上述损失函数,当计算一个隐特征向量时,固定其他变量.训练过程中Ut,V的更新公式分别如下:
(27)
(28)
最终,通过优化学习获得矩阵Ut与V,并将其代入式(20)获得最终的偏好预测矩阵.
5 实验结果与分析
5.1 数据集
本文实验采用Foursquare[20]和Gowalla[11]两个真实公开数据集来评估所提出模型的性能,其包含的相关内容如表1所示.为了评估算法的准确性,本文对数据进行预处理,分别去掉签到次数低于10个兴趣点的用户和低于10个用户签到的兴趣点.同时,本文实验按8∶2的比例将数据随机分成训练集与测试集.

表1 数据集统计Table 1 Statistics of dataset
5.2 评价标准
本文采用推荐算法中被广泛使用的两个评价指标:准确率precision@k与召回率recall@k,这里的k表示推荐列表的长度.公式分别如下:
(29)
(30)
其中,R(u)表示本文算法计算训练集后获得的兴趣点推荐列表;T(u)表示用户在测试集上真实的兴趣点签到列表.
5.3 实验结果分析
为了验证本文提出的GB-TSP模型的推荐性能,选取了四种具有代表性的模型与本文提出的模型进行对比,具体描述如下:
1)LRT模型[13]:将时间因素融入到矩阵分解模型中.考虑用户签到行为具有时间差异性和连续性两大特征,分别对其建模,最终将两个模型统一融入到矩阵分解模型中.
2)ASMF模型[9]:采用“两步走”的框架,首先利用用户偏好和地理信息为每个用户学习一组潜在兴趣点,将其填充进矩阵.再将地理因素与通过矩阵分解算法获得的偏好矩阵结合,完成推荐.
3)TACF模型[11]:首先将时间因素融入到基于用户的协同过滤推荐框架中,再将兴趣点流行度融入到基于幂律分布的地理模型中.最终生成一个融合时间和空间模型的统一模型,将签到分数最高的兴趣点推荐给用户.
4)LRBTSP模型[12]:首先利用时间特征建模用户对兴趣点的签到偏好,再结合流行度特征的影响,利用最近邻候选兴趣点方法建模空间模型.最终获得一个综合时间、空间和兴趣点流行度特征的模型.
实验1.参数分析
本节主要分析参数β对实验结果的影响.在矩阵填充阶段计算用户对兴趣点综合得分Su,t,l的公式(19)中,β∈[0,1]用来表示调整时间和空间影响的权重参数,其值的大小最终决定了兴趣点的得分及填充的结果.图2、图3为β取不同的值对Foursquare和Gowalla数据集中用户的top-5推荐的准确率和召回率的影响.从图2和图3可以看出,Foursquare数据集对应的准确率和召回率在β=0.8达到最好效果,而Gowalla数据集则在β=0.7时达到最好效果.两大数据集上的实验结果表明了参数的最优值会受到数据集的影响,因此在选取参数值时应当依据不同数据集最优选取.同时,实验还表明了用户对兴趣点的综合得分中的时间影响权重高于空间影响,这主要因为用户的偏好随时间表现出不同的行为模式,且受到数据稀疏的影响,采用均衡接近度的方法在缓解稀疏问题上发挥有效作用,使得时间影响占较大权重.但空间因素决定了用户在物理距离上的敏感性,对用户选择的兴趣点起到重要作用,不容忽视.因此本文在之后利用Foursquare和Gowalla数据集进行对照实验中,分别将β设置为0.8和0.7.
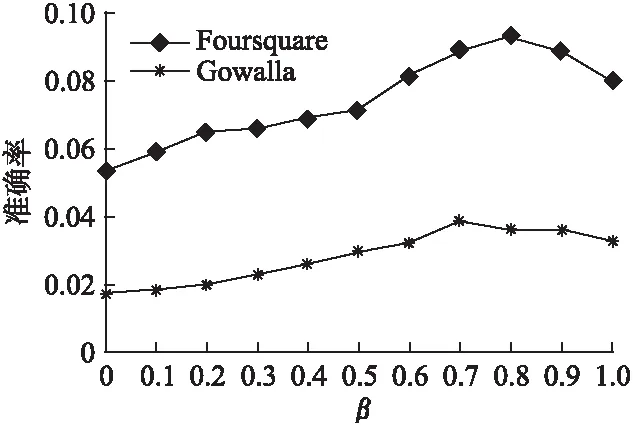
图2 不同β值对准确率的影响Fig.2 Influence of parameter β on precision
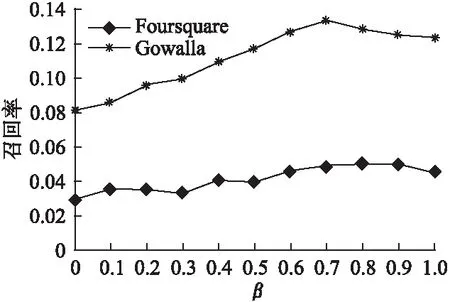
图3 不同β值对召回率的影响Fig.3 Influence of parameter β on recall
本实验中,对于正则化参数λu,λv,λt根据文献[13]中的最优参数分别设置为2,2,1;参数η和θ根据文献[9]中的最优参数预设置为10和0.1,经实验测试同样适用于本文模型;参数α表示兴趣点流行度的重要程度,在其他参数固定的情况下,实验通过从0到1每增加0.1来获取α值,通过测试不同α值下GB-TSP模型的准确率和召回率,发现α=0.5时的推荐性能最好.
实验2.验证矩阵填充的有效性
本节对第一阶段提出的矩阵填充模型的有效性加以验证,将待填充兴趣点的数量s设置为100,通过实验分析填充前后的推荐性能.实验分别在Foursquare和Gowalla数据集上比较k=5、8、10、12、15和20时,GB-TSP模型在填充兴趣点前后的准确率和召回率的变化情况,并在实验中将算法的其他参数设为最优值.
图4、图5分别是本文模型在Foursquare和Gowalla数据集上,通过填充矩阵前后的准确率和召回率的变化情况.两大数据集的实验结果表明,经过第一阶段的矩阵填充后的模型的推荐性能明显优于未经过填充的模型的性能,且在Foursquare数据集上变化更大,说明矩阵填充有积极意义.矩阵填充能明显提高推荐性能的原因主要是本文将时间划分后会导致严重的数据稀疏问题,通过第一阶段的矩阵填充能有效缓解数据稀疏性,同时运用均衡接近度方法能有效处理复杂贫信息系统的数据,对推荐性能的提高起到重要作用.

图4 矩阵填充对GB-TSP模型准确率的影响Fig.4 Influence of matrix filling on precision of GB-TSP model
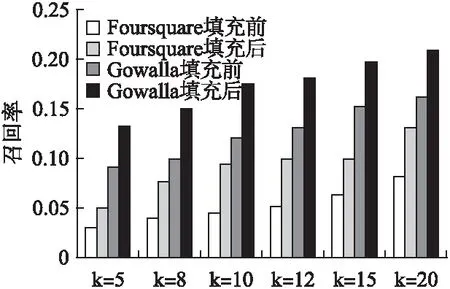
图5 矩阵填充对GB-TSP模型召回率的影响Fig.5 Influence of matrix filling on recall of GB-TSP model
实验3.不同推荐模型的性能对比
本部分实验分别在Foursquare和Gowalla数据集的基础上对五种推荐模型的性能进行了对比,并参照其他四种文献设置的不同参数,使各模型都取得最佳性能,对比结果见图6-图9.图6、图7和图8、图9分别展示了各模型在Foursquare和Gowalla数据集的基础上,兴趣点推荐列表长度k=5、8、10、12、15和20时的推荐性能.从图6-图9中看出,GB-TSP模型在两大数据集上的准确率和召回率均高于其他模型.随着k的增加,各模型的准确率在逐渐下降与召回率在逐渐升高.这主要是向用户推荐更多兴趣点有利于用户挖掘更多兴趣点,由此促进用户签到次数的增加,对准确率和召回率产生一定影响.

图6 Foursquare上不同推荐模型的准确率对比Fig.6 Precision of recommendation models on Foursquare
由图6-图9看出,本文所提出的GB-TSP模型的准确率和召回率明显优于其他四种模型.其中,LRT模型推荐性能均低于其他模型,由于只考虑时间因素,且利用时间段划分矩阵会造成更严重的稀疏问题.因此,LRT模型的推荐性能最低.ASMF模型考虑地理和社交因素,为用户学习一组待填充兴趣点,缓解数据稀疏性.因此,ASMF模型的推荐性能在Foursquare和Gowalla数据集上都明显优于LRT.但ASMF模型未考虑时间因素,无法为用户实现实时推荐.同前两个模型相比,TACF模型有效融合了时间、地理和兴趣点流行度,并将兴趣点流行度融入基于幂律分布的地理模型中.因此,TACF的推荐效果有一定改善,且从图8、图9看出,TACF模型在Gowalla数据集上表现更好.与TACF模型不同,LRBTSP模型采用最近邻候选兴趣点的方法建模用户的地理偏好,一定程度上提高了推荐精度,在Foursquare和Gowalla数据集均表现良好,但数据稀疏问题有待缓解.本文提出的模型有效改进了上述四种模型的不足.同LRT模型相比,GB-TSP模型考虑了更多的情景信息,并且通过矩阵填充缓解数据稀疏性.同ASMF相比,GB-TSP充分考虑时间的影响,解决了用户兴趣变化的问题.另外,GB-TSP在TACF和LRBTSP的基础上考虑了矩阵填充阶段,并将均衡接近度方法灵活地运用到时间影响模型中,有效缓解了数据稀疏的问题.同时,GB-TSP模型将时间影响充分地融入基于用户的协同过滤算法和矩阵分解算法中,达到了实时推荐的效果.因此,GB-TSP模型的推荐效果均优于其他四种模型,表现出最高的准确率和召回率.

图7 Foursquare上不同推荐模型的召回率对比Fig.7 Recall of recommendation models on Foursquare
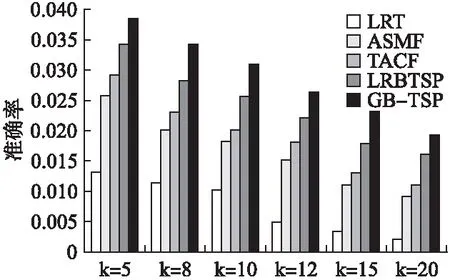
图8 Gowalla上不同推荐模型的准确率对比Fig.8 Precision of recommendation models on Gowalla
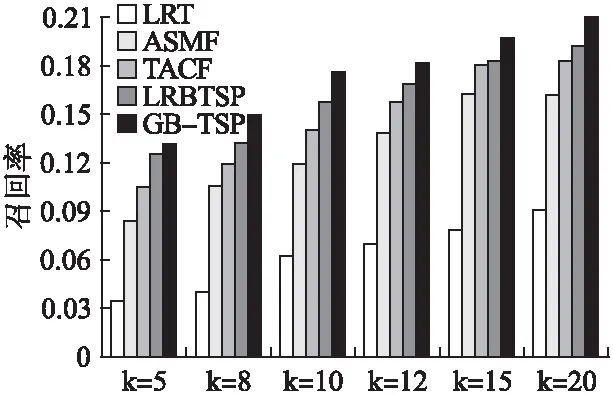
图9 Gowalla上不同推荐模型的召回率对比Fig.9 Recall of recommendation models on Gowalla
6 结束语
对于兴趣点推荐中的数据稀疏问题和用户兴趣的动态变化问题,本文提出了一种基于均衡接近度增强时间的兴趣点推荐模型.该模型在基准模型的基础上,利用均衡接近度方法增强时间接近度,将时间因素融入矩阵填充和矩阵分解两个阶段,实现实时推荐的效果.在Foursquare和Gowalla数据集上的实验结果表明,本文提出的模型有效地整合了多种情景信息,与其他基准的推荐模型相比,该模型的准确率和召回率明显提高.在接下来的工作中,将把异地推荐问题作为突破重点.同时,将深度学习融合到兴趣点推荐中也是一个值得研究的方向.
