一道立体几何最值问题解法探究

曹永生 杨刚 区卓君

[摘  要] 立体几何板块是高考考查的一个重要板块，经常出现在解答题第二道的位置，一般不会太难，学生往往也不会太过重视，甚至是忽略，但近年常以选填的压轴题形式出现，令很多学生望而却步，萌生放弃作答的念头. 这就要求我们在平时的教学中有意识地培养学生对该模块的经典问题进行总结，形成解题套路，完善知识体系，达到解一题通一类题的目的.

[关键词] 立体几何;公垂线;向量;不等式;高考

某次测试将立体几何题放在填空题倒数第二题的位置，学生普遍反映比较难，一是计算难，二是转化难，三是方法难. 本文介绍这道题目的变式及多种解法，让学生感受立体几何板块的综合性，让学生学有所思，总结一类题的解决办法，完善自己的知识体系.

测试题的题源及变式

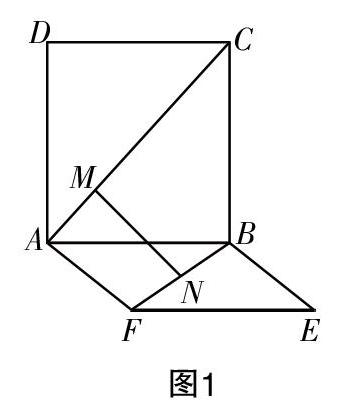
（测试题题源）在如图1所示实验装置中，正方形框架的边长都是1，且平面ABCD⊥平面ABEF，活动弹子M，N分别在正方形對角线AC，BF上移动，若CM=BN=a（0

（测试题）在如图2所示实验装置中，正方形框架的边长都是1，且平面ABCD⊥平面ABEF，活动弹子M，N分别在正方形对角线AC，BF上移动，则MN长度的最小值是__________.

测试题的几种解法

这道题是求两条异面的线段之间的距离，与异面直线的距离问题存在密切的联系，解法较多.

解法1（如图3）：作出公垂线段

取AB的中点G，设AC与DG交于M，BF与EG交于N.

由△DCM与△GAM相似得■=2，同理■=2，

所以MN∥DE.

又DE⊥AC，DE⊥BF（由三垂线定理易得），

所以MN是AC与BF的公垂线段，MN=■DE=■. ？摇？摇？摇？摇？摇？摇？摇？摇

解法2（如图4）：函数法

在AC上任取一点M，作MP⊥AB，PN⊥BF，MP⊥AB，PN⊥BF，则MN⊥BF.

设AP=x，则MP=x，BP=1-x，PN=■.

所以MN2=MP2+PN2=x2+■=■·x-■2+■.

当x=■时，MN的最小值为■.

解法3（如图5）：解析法

设M（0，a，a），N（b，1-b，0），由柯西不等式

MN2=b2+（1-a-b）2+a2≥■[b+（1-a-b）+a]2=■，

当且仅当a=b=■时等号成立，

所以MN的最小值为■.

注：本质上，解法3与下面的解法4是相同的.

解法4（如图6）：

作MP⊥AB，NQ⊥AB.

设AP=x，BQ=y，PQ=z（当AQPB依次排列时，z<0），则x+y+z=1，

MN2=x2+y2+z2≥■（x+y+z）2=■，

当且仅当x=y=z=■时等号成立，

所以MN的最小值为■.

注：解法4用到了以下公式的特殊情况（如图7）：

MN=■，

其中θ为二面角的平面角.

解法5（如图8）：向量法

设M（0，a，a），N（b，1-b，0），则

■=（b，1-b-a，-a），■=（0，1，1），■=（1，-1，0）.

由■·■=0得2a+b=1;

由■·■=0得a+2b=1，

解得a=b=■，即M0，■，■，N■，■，0，

所以MN=■.

若把本题改成求异面直线AC与BF的距离，则有以下解法.

解法6（如图9）：转化为线面距离，再转化为点面距离

因为BF∥平面ACG，

所以异面直线AC与BF的距离即为BF到平面ACG的距离，即点F到平面ACG的距离.

由V■=V■得■×■（■）2d=■×■×1，所以d=■.

解法7（如图10）：转化为面面距离

所求距离为平面ACG与平面HFB的距离，此距离为正方体体对角线的■，即■.

解法8（如图11）：向量法

■=（0，1，1），■=（1，-1，0）.

设与这两条异面直线都垂直得法向量为n，

则n·■=0，n·■=0，可取n=（1，1，-1）.

又■=（1，0，0），

所以d=■=■.

教学反思

总体而言，上述给出的8种不同的方法，分别从公垂线段，解析法，函数法，向量法，线面距离，面面距离等角度来解答本题，可谓是灵活多变，花样百出，能够使学生开阔思路，把学过的知识和方法融会贯通，使用自如，大大提升分析问题和解决问题的能力. 一题多解可以培养学生灵活、敏捷的思维能力，让学生学会对问题进行多角度、多层次的分析，达到对问题的全面理解，进而迅速准确地解决问题. 通过一题多解的训练，可以培养学生的发散性思维及联想能力，学会用不同的知识解决同一个问题，达到对多种知识的融会贯通，构建知识体系.

结束语

这道立体几何最值问题，笔者给出了8种不同的解法，对学生进行发散性思维训练. 最值问题通常跟不等式，函数，导数以及某些量的几何意义有着关联，内容相对比较复杂，形式相对多样，题目的综合性也比较强. 因此，在对高三学生进行立体几何专题复习时，除了对立体几何板块本身练习外，还需要给学生讲解立体几何与其他板块的联系，让学生能够在头脑中建立相应的知识网络结构，并且给予学生相应的立体几何板块的综合练习，使学生能够从不同的角度切入问题并选择合适自己的方法解决问题.