让数学课堂充满生机的有效策略

董桂霞

[摘  要] 新课程呼唤充满生机的数学课堂，倡导让学生成为课堂的主人. 这就要求教育者设问题激起学生的学习兴趣，以固课堂之“根”;设疑于出错处、困惑处或难点处，激起学生的探究欲望，以固课堂之“魂”;引导学生积极主动参与到学习中去，成为生机勃勃的探索者，以固课堂之“本”;尊重学生和欣赏学生，让爱心点燃学生的探究之火，最终让课堂充满生命活力.

[关键词] 数学课堂;充满生机;有效策略

新课程改革实施以来，课堂教学虽然发生了巨大的变化，但传统教学观念仍然影响着课堂教学，课堂教学仍然存在着一些问题，主要表现在：教学过程仍然以“知识核心”的教学观念为主体;教师仍然是课堂的重心，并单向性地向学生传授知识，毫无生机;学生被动接受知识，深感学习枯燥乏味，学习效果不够理想. 那么，如何有效解决上述问题，让数学课堂充满生机呢？这成了当前众多一线教育工作者研究的重要课题. 基于此，笔者结合实践经验与资料参考，构建了一条充满活力的教学模式，以期能够为高中数学教学提供一些有效策略与建议.

问题——让课堂充满生机之“根”

从教数十年，笔者观摩过各式课堂，其中不乏一些大型的观摩课、大赛课等，很多时候都会被执教教师精彩的教学设计而折服. 通常，他们都有着新颖且精妙的问题设计，宽松且紧凑的教学时空，井然有序的教学步骤，让学生在积极愉悦的学习氛围中体验到了“学数学”与“用数学”的乐趣. 笔者认为，一节优质课除去教师深厚的基本功及扎实的课堂驾驭能力之外，最为关键的就是问题设计的技巧与方式. 问题是激发好奇心，启动思维的“利器”，是教学活动推进的载体，是培养学生良好学习习惯的“催化剂”，因此数学教学应以问题为根基去营造心理困境，引导学生去发现、去建构、去应用，让课堂充满生机.

例如，学习“映射”这个抽象概念，执教者创设以下问题情境：“一个人的名字仅仅是一个代号，那这个人与其名之间则存在着一种对应关系，你所知道的还有哪些对应关系呢？”多次实践证明，教师创设的问题情境指向性越高，则越能激发学生的求知欲，使得建构活动朝着理想的方向快速推进，使得课堂教学生动活泼，使得教学目标快速达成. 通过以上的问题情境，有利于学生快速理解“映射”这个抽象概念，让概念的形成真正源于学生的亲身感受与体验.

又如，学习“空间几何体的表面积”，执教者抛出以下问题：“现在王师傅需要在一个空间几何体的表面刷上一层油漆，那么你们觉得应该如何计算所需用的油漆量呢？”从学生熟悉的事物出发，激发探求新知的欲望，这样的问题情境，不仅呈现了本课的教学重点，还让学生以一个数学家的角色进入探究状态，无疑会引起他们的兴趣.

设疑——让课堂充满生机之“魂”

心理学家贝恩布里奇曾说：“差错人皆有之，作为教师不利用是不可原谅的.”传统课堂教学中，教师讲解与示范，学生记忆与消化，学生在运用新知识时不出错，这算得上一堂好课吗？这样的课堂算是成功的吗？事实上，教师并非预言家，不可能预知学生所有的错误，只有巧设疑问展开教学，设疑于学生的出错处，设疑于学生的困惑处，设疑于教学的重难点，让学生不断碰壁，才能给予学生从事数学活动的机会，才能让学生感受到数学探究的快感，才能让学生感受到先痛后快的愉悦，这样的课堂才能意味无穷[1].

例1：已知圆O1的方程为x2+（y+1）2=4，圆O2的圆心坐标为（2，1），若圆O1与圆O2相交于点A和B，且AB=2■，试求出圆O2的方程.

本题所涉知识为两圆相交的弦长，学生易想到通过作图法去构造直角三角形来构建解题路径. 学生经过一番思考后开始解题，教师来回巡视中，发现以下错解，并板演.

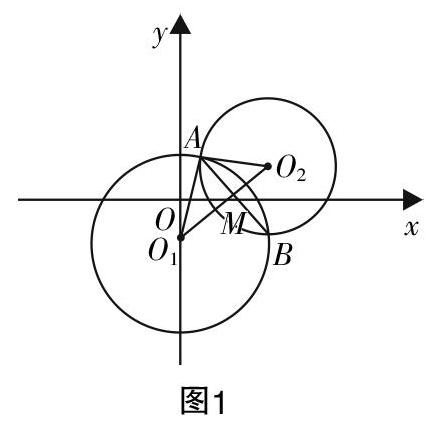
错解：如图1，连接AB，O1O2，AO1，AO2，其中O1O2与AB交于点M.

Rt△AMO1中，O1A=2，AM=■AB=■，则MO1=■. 而O1（0，-1），O2（2，1），则O1O2=2■，所以MO2=■.

Rt△AMO2中，AO2=2. 又因为圆O2的圆心O2（2，1），半径为2，所以圆O2的方程为（x-2）2+（y-1）2=4.

师：以上解题思路正确吗？（学生纷纷进入观察与思考状态）

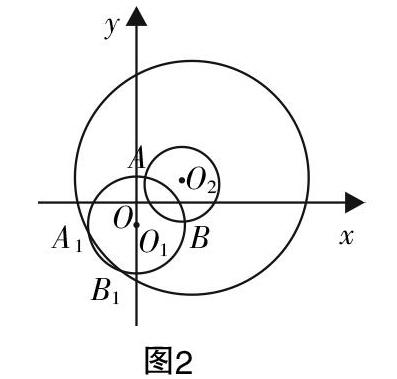
生1：他存在漏解的问题，如图2，这样的大圆也可使得相交的弦长为2■.

师：很好，那能和大家说一说正确的解题思路吗？

生1：设圆O2的方程为（x-2）2+（y-1）2=r2，則有x2+y2+2y-3=0，x2+y2-4x-2y+5-r2=0.消去x2，y2，可得两圆相交弦AB所在的直线方程为x+y-2+■=0，则O2（2，1）到直线AB的距离为d=■=■，解得r2=4或r2=20. 所以，圆O2的方程为（x-2）2+（y-1）2=4或（x-2）2+（y-1）2=20.

反思：事实上，关注通性通法才是好的数学教学，才是高考命题始终坚持的原则. 不少教师热衷于“一题多解”，却摒弃了通性通法，使学生的注意力始终停留在“题型+技巧”上，完全忽视了解题的根本. 以上例题中，让学生去联想通性通法，并透过问题的表象看到问题本质，从一般性解题思路去解析问题，这才是解题教学的长远利益.

参与——让课堂充满生机之“本”

新课程改革将学生从“授业”的枯燥课堂中解放出来，让学生积极主动地参与到学习活动中来，让学生成为学习的真正主人. 他们不再是被动的倾听者，而是生机勃勃的探究者，是学习真正的主人[2]. 因此，在数学课堂教学中，教师需点燃学生的学习热情，让学生主动参与，让数学课堂焕发它应有的光彩.

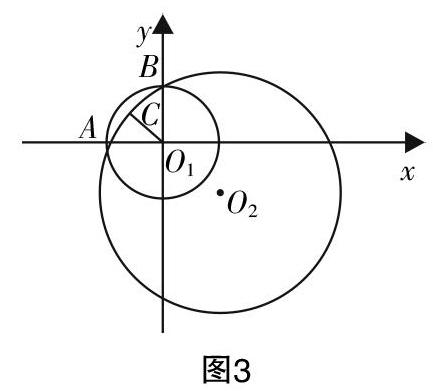
例2：如图3，已知圆O1：x2+y2-4=0与圆O2：x2+y2-4x+4y-12=0，试求出圆O1和圆O2的公共弦长及所在直线方程.

求两直线交点的问题，常用方法为联立方程得出交点坐标. 本例中要求的是两圆公共弦长与所在直线方程，类比以上方法则可以联立两圆的方程进一步求解.

解：联立方程组x2+y2-4=0，x2+y2-4x+4y-12=0，消去x2，y2，可得x-y+2=0，即y=x+2. 再将其代入x2+y2-4=0，可得x2+2x=0，解得x= -2或x=0. 所以两圆的交点为A（-2，0），B（0，2），公共弦长为AB=2■，公共弦所在直线方程为x-y+2=0.

反思：上述例题中的解法为一般解法，当遇到两圆方程消元后无法因式分解时，需借助求根公式求解的情形，交点坐标则会繁杂多了，那么就会影响进一步求两点距离与所在直线方程. 此时，教师可以带领学生审视以上解题过程：在处理方程组进行消元时，由于代入法有困难，便消去x2，y2，得到关于x，y的一元二次方程，而所得点A（0，2），B（-2，0），满足方程y=x+2，据此可得该二元一次方程即为两圆公共弦所在直线方程.

情感——让课堂充满生机之“源”

积极的情感可以充分调动学习的激情，是学生产生学习内驱力的源泉. 在课堂教学中，教师应以平等的态度去尊重学生和欣赏学生，满足学生的表现欲与言论欲，鼓励学生大胆创新，用自己的爱心点燃学生的探究之火.

例3：命题p：？坌x∈[1，2]，■x2-lnx-a≥0是真命题，试求出a的取值范围.

师：请大家思考并说一说解题思路.

生1：从函数f（x）=■x2-lnx-a，x∈[1，2]着手考虑，问题等价于“f（x）■≥0，求a的取值范围”，本题则可运用导数求解函数的最小值.

师：思路清晰，非常好！还有其他的解析方法吗？（此时教师充分展示“等待”的艺术，为学生留足思考时间，让其充分表达）

生2：分离变量a，x，则条件即可转化为“？坌x∈[1，2]，■x2-a≥lnx”. 令f（x）=■x2-a，g（x）=lnx，则在[1，2]上，函数f（x）的图像恒在函数g（x）的图像上方. 再观察图像，只需在x=1处，f（x）的函数值不小于g（x）的函数值即可.

师：生2的思路非常清楚，但是在解题的过程中，有些细节的处理还未到火候. 一个就是恒等变形不等式时，未实现分离变量的目的;第二个就是在[1，2]上，函数f（x）的图像恒在函数g（x）的图像上方时，为什么只需f（1）≥g（1）？根据上述的提示，你认为问题可作如何的变换？

生2：我知道了，在分离变量时，命题可转化为“？坌x∈[1，2]，a≤■x2-lnx，则a≤■x2-lnx■，x∈[1，2]”，这样一来，问题就简单多了！

师：多么漂亮的思路啊！

……

反思：以上说明，在课堂中教师与学生是平等的，教师既要给予学生充分的尊重，还需要掌握好“等待”艺术，让学生体会到学习的愉悦和成就感.

总之，有效的教学策略决定着教学的达成度，关系的学生思维活动的开展度，影响着教学的效果. 教师在课堂中需采用多种教学策略唤起学生的学习兴趣，如精心设问、精心设疑等，让学生积极参与，主动思维，与此同时还需尊重学生、信任学生和欣赏学生，从而使学有成效，让课堂充满生机.

參考文献：

[1]  田松华. 例谈数学课堂如何巧妙设疑[J]. 中学教学参考，2011（10）.

[2]  瞿兵. 课堂教学实施“主体参与”的探索与研究[J]. 教育科学，2000（02）.