数学文化视角下高中解析几何教学策略探讨

苏燕

[摘  要] 渗透数学文化是高中数学教学实现素质教育的有效途径.文章以圆锥曲线专题解题教学为例，探讨了数学文化视角下高中解析几何教学策略. 认为在具体教学实践中，教师应不断丰富数学文化素材、加强数学文化背景、提炼数学文化核心，只有这样，才能帮助学生在培养科学素养的同时实现人文素养，才能达到“以数化人”的素质教育最终目的.

[關键词] 高中数学;数学文化;解析几何

数学教学中融入数学文化，可以有效帮助学生提高数学与社会发展关系的认识，不断开阔学生的视野，进而帮助学生实现数学学科核心素养. 而在当前数学文化渗透教学实践中，教材中数学文化的设置基本上成为摆设，数学文化素材极度缺乏，致使相当数量的学生对数学本质和数学思想理解不深，对数学学习兴趣不浓，并且错误的数学价值观、数学思维发展受限等问题在一定程度上还存在. 因此在具体教学实践中，教师应不断丰富数学文化素材，加强数学文化背景，提炼数学文化核心，只有这样才能帮助学生在培养数学素养的同时使学生的思想素养、文化素养均得到有效提升，才能达到“以数化人”的素质教育最终目的.

数学文化视角下高中解析几何教学策略

1. 概念教学中丰富数学文化素材

由于数学文化的引入，学生对数学学习的兴趣会得到大幅度提升，但是，现实中可以供教师选择的有关数学文化素材寥寥无几，并且所选择的素材大多与教学内容无关，因此，为了有效避免上述教学中所面临的困惑，教师应在概念教学中不断提高素材的数学文化背景. 在具体教学实践中，一是在选取素材时注重数学文化、数学问题、数学知识的难易程度，素材内容主要以介绍数学精神、方法以及思想为主;二是为了让学生体会数学美的价值，教师在渗透数学文化时应以蕴含其中的思想、方法为主，而不是简单介绍数学家的生迹以及历史记录;三是素材的选取应注重与其他学科的融合，要使学生的思想素养、文化素养以及数学素养均得到有效提升.

2. 例题设计中加强数学文化背景

由于具有题源性的特点，教材中的例题以及课外习题是教师呈现数学文化的主要方式，因此，为了帮助学生理解数学本质，提升学生的学习效率，教师应在例题教学中加强数学文化背景的教学. 例如，教师可以现实生活为基础，以教学内容为依据，通过编制以数学文化为背景的试题，将学生所要掌握的数学知识技能与数学故事本身联系起来，将数学文化与所要考查的内容结合起来，进而培养学生的数学价值观.值得说明的是，将数学文化融入试题教学之中，并不是要求教师对所呈现的试题加以编造故事，而是渗透某个数学思想和数学方法，或者是在题面上有明显表示即可.

3. 数学价值导引中发挥数学文学特性

为了促进学生学习的主动性，充分发挥数学文化指导生活实践的作用，教师应在教学过程中将承载数学文化功能的视频或图片与教学价值融合起来[1]，并通过一些数学与日常生活相互联系、相互作用的典型案例，有效改变学生对数学知识只能被用作考试的错误观念，不断促使学生在数学价值引导中发挥数学文学特性.

4. 数学思想贯穿中提炼数学文化核心

教学实践中，数学思想的渗透明显多于数学价值、数学文化、数学美的渗透，加之数学思想的教学一直受到广大教师的重视，因此，教师在各个环节中都应重视数学思想的渗透，充分挖掘数学家在生成相应观点时的重要数学思想，让学生在有效掌握数学知识的同时体会其所蕴含的核心数学思想，从而通过这些数学核心思想建立起复杂的知识系统.

5. 感受数学美中丰富的数学文化

数学文化的渗透可以让学生体验到数学美，可以激发学生探究的兴趣，有效增进学生的眼界，因此，教师应通过设计例题的形式，让学生在推理或运算中感受整体美、和谐美. 同时，教师还应多设置一些展示数学文化的校内活动，充分应用阅读思考、探究与发现、信息技术与应用等载体，让学生在体会数学美的同时进一步掌握数学知识的本质.例如，为了让学生真实感受到数学文化的重要性，教师可以要求学生制作以数学文化为核心的幻灯片、演讲报告等. 同时，还可以设置每月一次的数学文化周，切实让学生发自内心感受数学文化的重要性.

数学文化视角下高中解析几何教学实践

仅有相关理论是不够的，而解析几何蕴藏着丰富的数学思想，并且对于数学的发展起着分水岭的作用，在一定程度上是提高学生科学素养和文化素养的典型内容. 下面，笔者以圆锥曲线专题解题教学为例进行深入探讨.

1. 介绍圆锥曲线的重要数学史和具体应用

为了激发学生学习的兴趣，引导学生主动参与教学，笔者利用幻灯片的形式呈现了如下人物和具体史料，即阿基米德、欧几里得、阿波罗尼斯，并介绍了解析几何创立之后，代数的二元二次方程就是圆锥曲线，从而使得圆锥曲线的研究摆脱了几何直观而向抽象领域迈进[2]. 同时，还以图片的形式介绍了圆锥曲线在声、光、热、电等方面的物理学特性，展示了现实生活中太阳能光电站、音乐台、太阳灶以及灯具与望远镜的设计.

2. 设置问题链深度探究圆锥曲线问题

为了强化阿波罗尼斯对圆锥曲线的重要贡献，阐述高考命制试题的重要题材，有效拓宽学生学习的知识面，笔者设计了如下问题，要求学生以小组为单位自行探究. 在此过程中，教师对于有困难的小组及时给予提示和帮助，对于能够解决的小组要求及时归纳总结.

（1）已知⊙O：x2+y2=1，A（-2，0），B（b，0）（b≠2），若对⊙O上的任意一点M，恒有MB=λMA，则试求b和λ的值.

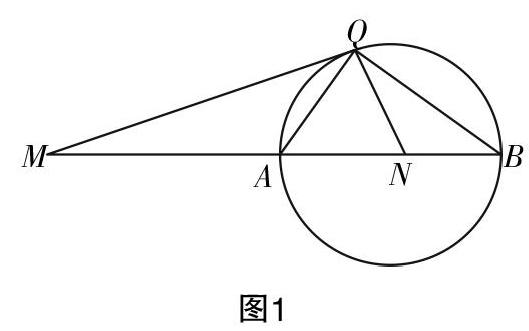
（2）如图1所示，已知M，N为平面上不同的两点，若一动点M在平面上满足■=λ，若λ>0且λ≠1时，试证明点Q的轨迹是圆.

（3）已知F1，F2是椭圆■+■=1（a>b>0）上的两个焦点，椭圆与x轴的交点分别为A1（-a，0），A2（a，0），点T1，■为椭圆上的一点，并且TF2的斜率不存在.

①试求a，b的值.

②若点P为椭圆上异于A1，A2的一点，并且A1P，A2P与直线l：x=t（t为定值）的交点为点M，N，点Q为直线l上的一点，若PQ与椭圆有且仅有一个公共点P，那么Q一定平分MN. 请根据上述命题表述出它的逆命题，并判断该命题的真假.

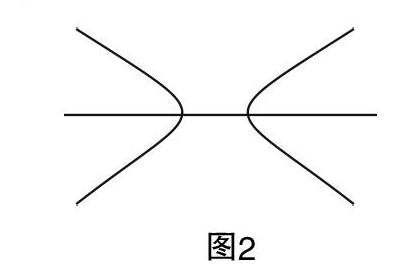
③如图2所示，根据上述解题思路，试作出与该双曲线有且仅有一个交点S的直线m.

显然以上习题的设置，从不同角度将数学美、数学史、数学价值以及数学思想融入其中[3]，呈现了阿波罗尼斯圆等数学文化背景，充分展示了要有效解决上述问题仅靠数学知识是不够的，在具体解题过程中，还要有意识地结合数学文化的史实性、价值性、工具性等系统.

3. 创设圆锥曲线课外教学活动

为了营造良好的具有解析几何味道的数学文化氛围，有效配合课内解析几何教学，笔者要求学生根据所学知识，以小组为基本单位，撰写一篇与圆锥曲线相关的数学文化文章，对于一些优秀的数学文化成果在学校的校园网上公开展示. 值得注意的是，在文章撰写中，要体现出以下三个方面：一是与课内教学内容有关;二是能改善和促进学生的数学思维;三是问题能涉及和揭示数学的本质.

总之，数学文化视角下高中解析几何教学能够改变学生对数学学习的看法，有效提升学生对知识本质的理解，因此，在具体教学实践中，教师应不断丰富数学文化素材，加强数学文化背景，提炼数学文化核心. 只有这样，才能帮助学生在积累科学素养的同时实现人文素养的提升，才能达到“以数化人”的素质教育最终目的.

参考文献：

[1]  施炜. 从知识的三要素看高中数学学科核心素养的培育[J]. 数学教学通讯，2019（33）.

[2]  赖白雪. 数学文化视阈下的高中数学教学策略研究[D]. 重庆师范大学，2019（5）.

[3]  周波. 高中数学实施数学文化教育的思考[J]. 数学教学通讯，2017（18）.