聚焦数学知识的绘本阅读指导
2020-10-20桂华


【摘要】本文以指导小学生阅读数学绘本《两条射线手拉手》为例,论述教师引导学生在阅读数学绘本过程中聚焦数学知识进行阅读和思考的策略,提出讨论封面图和标题、讨论并总结故事情节、开展操作活动、追问数学问题以及绘制数学画等建议。
【关键词】数学绘本 数学知识 《两条射线手拉手》
阅读与思考
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2020)29-0080-03
数学绘本通过贴近儿童生活的趣味故事内容和色彩丰富的直观图画形式,向读者讲述数学知识。阅读数学绘本能激发学生数学阅读的兴趣,让学生在不知不觉中学习数学知识,受到数学思想的熏陶。低年级的学生处于直观形象思维为主的阶段,教师可以选择数学绘本指导学生进行数学阅读,引导学生在阅读绘本故事中思考,初步学习数学信息的提取、转译和内化,实现数学意义的个人构建。然而笔者在研究中发现,学生在阅读数学绘本时,更关注人物和故事情节,对于较难理解的数学知识往往会略过。基于此,笔者以《两条射线手拉手》小学数学绘本阅读指导为例,说明教师如何引导学生在数学绘本阅读中聚焦数学知识阅读和思考。
一、讨论封面图和标题
绘本的封面一般蕴含故事所要表达的主要信息。我们可以让学生仔细观察封面上画了什么,读一读题目并将题目和画面结合起来,猜一猜这本书是讲什么的、会发生什么故事,等等。
《两条射线手拉手》封面隐藏着“两条射线手拉手”形成的角,乌龟、鳄鱼、小鸟的嘴巴有角,鳄鱼的背上有角……然而这些都会被学生忽略,因为学生并没有“角”的经验。学生最先看到的是鳄鱼和乌龟,进而发挥他们的想象,猜测这两个动物之间发生的故事。教师可以让学生读一读故事的题目,提问:“你知道什么是射线吗?”“两条射线手拉手会变成什么呢?在这个封面藏着答案,找一找,你发现了吗?”
学生的数学知识基础决定了他们对文本中数学知识的理解,如果学生不知道什么是射线,也就无法建立角的概念,就不能比较准确地预测绘本的主要内容。教师可以先带领学生阅读绘本的第一页。“我是射线伊伊,我们射线不会弯曲也不会转折。有一个固定的端点,另一端可以无限延伸。”学生观察绘本第一页的图,认识了射线伊伊,教师再让学生在封面上找到伊伊。在这个基础上,教师告诉学生封面上就藏着两条射线手拉手组成的图形:“你能找到它的名字吗?能找到这样的图吗?”学生会迅速找到“角”这个字,并有意识地寻找并发现乌龟、鳄鱼、小鸟嘴巴上的角以及鳄鱼背上的角、向日葵钟面上的角、坐在圆球上的小人儿的帽子上的角……绘本中的图画包含着丰富的细节,这些细节均突出故事的主题。教师要引导学生观察画的细节,从视觉图像的视角理解文本内容。在这样的指导下,学生不仅能发现物体上的角,还能找到三角形、梯形等平面图形中的角。学生虽不会准确地表述角的概念,但能感悟到像这样两条射线接在一起,有一头尖的就是角。
教师再追问:“请将题目和刚才观察到的信息结合起来,再猜一猜,这本书会讲什么呢?”学生会修正原来的猜测,重新猜测两条射线为什么要手拉手?射线拉手形成角后有哪些奇遇?会联系鳄鱼和乌龟张开嘴形成角吃东西等情景,猜测发生的趣事,感悟到预测不是随便乱猜,而是观察、收集信息、思考后进行预测。这样的预测会将学生吸引到故事中去,让他们变成一个个积极主动的阅读者,他们会有目的地读书,并希望知道自己的预测能否被验证,是否要根据新的信息不断修正自己的预测。随着阅读的继续,我们逐步明确了故事要素:谁、何时、何地、是什么、为什么。教师可以再次询问学生是否需要修改预测,并让其解释自己的想法。教师所要做的,就是将学生的预测转化为一种有意的行为,然后通过反复练习,让他们将此策略融入自己的阅读中,促使学生不断思考,帮助学生去理解故事。
二、讨论并总结故事情节
在引导学生阅读的过程中,教师可以在学生阅读完一个段落后暂停,引导学生讨论、总结情节。但是并不是每个段落都需要这样做,否则会影响学生阅读的流畅性。教师可以在出现了数学知识或对学生而言较难理解的地方暂停,运用关键图文引导学生针对数学概念去讨论和总结,促进其进行有意识地阅读。
比较角的大小是学生认识角的一个难点,学生容易受到图形形状大小的干扰。《两条射线手拉手》设计了角“张嘴吃东西”的故事情境,帮助学生理解角的大小与角两条边张开的大小有关,如图2所示。教师可以在这里停下来,引导学生思考和讨论读到的内容:哪个角的两条边张开得大?想象“如果要吃更大的东西,伊伊和亚亚应该怎么做”……在这个基础上,教师可以让学生自主总结故事情节,让学生说说刚刚阅读的段落中的主要事件,或者说说自己的收获、哪个角大一些。大部分学生认为“水果越大张开的角就越大”,一部分学生认为“两条边张开得越大,角就越大”。这样的讨论和总结有助于学生将重要的数学知识和无关冗余的信息区分开来,这是数学绘本阅读的关键做法。
三、创设数学操作活动
荷兰数学家弗赖登塔尔指出:数学教育必须面向社会现实,必须与真实的生活情景相结合,必须注重培养学生从客观现象发现数学问题的能力。绘本之所以深受学生喜爱,是因为故事贴近学生的生活经验。数学绘本更是把生活数学融入故事中。教师可以按照“故事情景—数学知识—生活应用”的思路,将学生生活中已经建立起来的认知与绘本中的新数学知识进行联结,促使学生在阅读、比较、操作等自我经历中理解数学概念并将其运用于生活。
《两条射线手拉手》讲述了两条射線伊伊和亚亚做跑步抓人的游戏,形成了锐角、直角、平角和周角,介绍了角的度量单位。教师可以先带领学生阅读,然后比较形成的角有什么相同点和不同点,再提供两根小棒:“孩子们,你们能让手中的伊伊和亚亚也来做这个游戏吗?”让学生边操作边讲述故事。在这里,学生并不需要准确地表述和摆出90度的直角、180度的平角以及360度的周角,他们只是在自己感兴趣的活动中模仿表演伊伊和亚亚的跑步情况:将两根小棒重叠在一起,一根小棒不动,另一根小棒旋转模拟“跑步”,直观地触摸到一端不动形成的“顶点”,跑了半圈是半个圆,看起来像一条直线,半圆角度的一半是90度,跑了一圈又重合了,是360度。学生还可以让伊伊、亚亚出现不同的跑步结果,创造不同度数的角,充分操作,在“真实”的情境中进行知识的建构。最后,再让学生找一找身边的角。这样的操作活动要注意次数和时机,一本绘本有一至两个操作活动即可,操作可以放在阅读故事后进行。
四、追问数学问题
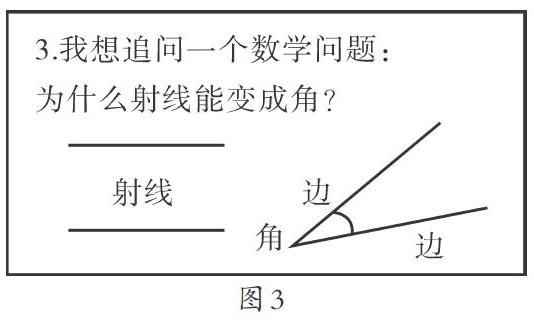
在指导學生阅读的整个过程中,教师要不断鼓励学生提问。我们强调“追问数学问题”,学生提的问题最好是与数学知识有关的,而且要基于绘本中的数学知识,与老师或其他同学交流讨论不明白的地方,追根究底地问、多次地问。有的学生在教师讲到角时追问:“什么是角?”教师可以根据学情停下来,提供更多素材,与学生一起交流讨论这个问题;有的学生在教师讲到角的度数时追问:“为什么角最大只有360度?最大1000度不行吗?”这可真是一个好问题。在大家都认为这就是规定,没有必要思考和质疑的时候,这名学生却不受约束,提出了这样的问题。这个问题引发教师和学生针对这个问题进行思考和查找资料,大家从而了解到这和60进制有关。还有一名学生在绘本阅读后,追问为什么射线能变成角(见图3)。这名学生画的两幅图都是由射线组成的图形,一幅是永不相交的两条射线组成的一组平行线,一幅是从一点引出两条射线,他不仅知道两条射线能组成角,还通过对比的方式说明两条射线并不是只能组成角。
问题对于学生思维的培养有重要意义,学生能在读中慎思,这才是有价值和意义的阅读。
五、绘制数学画
阅读绘本后,教师可以让学生用纸和笔根据自己最感兴趣的故事情节绘制一幅数学画。数学画让学生聚焦绘本中的数学知识并促进其进行再次梳理,同时也能检验学生对知识的理解程度。不同学生的阅读理解能力不同,阅读时关注的点也不同,呈现不同的认知。
图4、图5、图6是三名学生在阅读绘本后画的三幅数学画,三名学生关注点不同,对知识的理解程度不同。图4的作者关注的是生活中的角,自己创作了一个情景,呈现自己对角的认识;图5和图6的作者都关注到了角的大小,但是理解程度不一样,图5的作者只停留在“张嘴吃东西”,即还原故事情节的层面,图7的作者进了一步,虽然画存在问题,顶点没有重合,但是反映出作者能用重叠的方法比较角的大小。
教师还可以引导学生根据绘本中的图画和故事情节,想象接下来发生的故事,续编绘本,创作数学画。学生会运用自己通过阅读学习到的数学知识去想象、判断、分析,加深对绘本的理解,构建和运用数学知识,同时发展思辨能力和想象能力。
图7的作者创编了小老鼠吃三明治的数学画,呈现阅读到的数学概念——角,画出了一个直角三角形,数学画中隐藏着小惊喜——小老鼠的嘴巴是一个角。图8就更让人惊喜了,作者创作的是吃黄豆的故事情节,虽然用的仍然是原绘本中“所吃东西的大小不同,角的两边张开得越大角就越大”的情境,但是却改成了吃同一物体,大小一样,数量不同,7<9,用数形结合的方式得出结论。
值得注意的是,数学绘本的阅读要聚焦数学知识,在阅读中有思考,但千万不要执著于掌握数学知识而忽略了阅读数学绘本的乐趣,背离了通过绘本激发数学学习兴趣、寓教于乐的初衷。我们期望能做到的是:让学生学会主动思考的阅读方式,成为一名独立的阅读者,爱上数学阅读。
作者简介:桂华(1974— ),女,湖南祁阳人,大学本科学历,高级教师,研究方向为小学数学教学。
(责编 刘小瑗)
