基于三阶段DEA模型的长江干线主要港口效率评价

杜利楠　张建宝

摘要：为剔除環境变量和随机因素的影响，更加准确地评价港口效率，运用三阶段数据包络分析（data envelopment analysis，DEA）模型对2010年和2017年我国长江干线20个主要内河港口效率进行测度评价。结果表明：长江干线各主要港口，特别是长江干线中上游港口的规模效率相对较低，港口岸线资源、土地资源、设施设备和建设投资等要素投入相对分散，尚未形成规模效应;部分港口存在投入拥挤和产出水平低的现象，资源浪费问题突出。需要根据各港口发展实际，优化资源配置，提升港口效率。

关键词：长江干线; 效率评价; 环境变量; 数据包络分析（DEA）

中图分类号：  F552.7

文献标志码：A

Efficiency evaluation of main ports along Yangtze River

trunk line with three-stage DEA model

DU Linan， ZHANG Jianbao

（China Waterborne Transport Research Institute， Beijing 10088， China）

Abstract：

To eliminate the impact of environmental variables and random factors to evaluate the port efficiency more accurately， the three-stage data envelopment analysis （DEA） model is adopted to measure the efficiency of 20 major inland river ports along the Yangtze River trunk line in China in 2010 and 2017. The results show that： the scale efficiency of the major ports along the Yangtze River trunk line， especially the upper and middle reaches， is relatively low， the input of port shoreline resource， land resource， facilities and construction investment is relatively scattered， and the scale effect has not been formed; some ports are of heavy investment and low output， and the port resources are wasted seriously. It is necessary to optimize resource allocation and improve port efficiency according to the actual development of each port.

Key words：

Yangtze River trunk line; efficiency evaluation; environmental variable; data envelopment analysis （DEA）

0 引 言

长江是货运量位居全球内河第一的黄金水道，是我国内陆11个省市自治区的出海大通道，是连接西南、华中、华东三大经济区的交通运输大动脉。长江航运是长江经济带发展的重要依托，也是连接丝绸之路经济带和21世纪海上丝绸之路的重要纽带，在国家经济社会发展及综合交通运输体系中具有举足轻重的地位。

港口效率评价一直是交通经济、航运经济领域研究的热点问题。近年来，国内外学术界对港口绩效的研究方法不断丰富，其中数据包络分析（data envelopment analysis，DEA）是效率评价最重要的方法之一。国外文献对集装箱港口效率的研究较多，如：DE OLIVEIRA等[1]以200个集装箱港口为样本，利用DEA模型研究了在不同层面（地方、区域和全球层面）的竞争程度如何影响集装箱港口的效率;KUTIN等[2]利用DEA模型测算了东盟50个集装箱港口的相对效率;YUEN等[3]利用DEA估算样本集装箱码头的运行效率，重点分析了外国和地方所有权的参与和竞争如何影响集装箱码头效率。随着我国港口经济的快速发展，国内学者也越来越关注港口效率问题，如：庞瑞芝[4]利用生产率指数测算了我国沿海50个港口的动态效率;匡海波等[5]利用DEA和因子分析法测度了8个沿海港口的生产效率;沈金生等[6]利用三阶段DEA模型测算了环渤海地区主要港口效率，实证分析了港口综合效率受环境变量和随机因素的影响;王玲等[7]运用SBM（slack-based measurement）-DEA方法，对比分析了2006—2009年我国14个内河港口和17个沿海港口效率;王玲等[8]运用三阶段DEA方法对2008年我国主要内河港口的效率进行了实证研究;赖成寿等[9]采用二阶段DEA博弈交叉效率模型对17家上市港口企业进行了效率测度。

总之，已有研究多集中在沿海集装箱港口，对内河港口（特别是长江干线港口）效率的评价相对较少且缺少动态效率的比较分析;在指标选取时多考虑港口运营的相关指标，对外部环境因素考虑稍显不足。基于此，本文以长江干线20个港口为研究对象，运用三阶段DEA模型，剔除环境变量和随机因素对港口效率的影响，对比评价2010年和2017年我国长江干线主要港口效率，揭示港口效率变化和空间结构特征，研究结论对提升长江干线港口效率、更好地支撑长江经济带建设具有一定的参考价值。

1 研究方法與模型

DEA是根据多项投入指标和多项产出指标，利用线性规划的方法，对具有可比性的同类型单位进行相对有效性评价的一种数量分析方法。DEA方法最初由CHARNES等[10]于1978年提出，但该方法未考虑环境变量和随机因素对评价结果的影响。为提升模型评价结果的精确性，FRIED等[11]将环境影响和统计噪声引入模型，即三阶段DEA。

1.1 第一阶段：传统BCC-DEA建模

利用原始投入产出数据构建传统的BCC-DEA模型，即投入导向的规模保持可变模型[12]，测算得出初始综合效率。综合效率可分解为规模效率和纯技术效率，且综合效率为规模效率与纯技术效率的乘积。

1.2 第二阶段：随机前沿分析（SFA）

在传统DEA基础上，利用随机前沿分析（stochastic frontier analysis，SFA）法验证环境变量和随机因素的影响。在本阶段需要重点关注松弛变量，该变量由环境变量、管理无效率和统计噪声构成。构建SFA模型对环境变量进行回归分析，可判断上述3个因素的影响。

（1）建立松弛变量Sni：

Sni=xni-λxni （i=1，2，…，I;n=1，2，…，N）

式中：xni为第i个决策单元（decision making unit，DMU）的第n个投入值;

λxni为第i个DMU的第n个投入值在效率前沿面的最优映射。

（2）构造SFA回归模型：

式中：Zi 和βn分别表示环境变量及其系数;νni+μni是混合误差项，νni表示随机干扰项，μni表示管理无效率。

（3）调整投入变量：

式中：Xni和XAni分别表示调整前、后的投入;max f（Zi;β^n）-f（Zi;β^n）是对外部环境因素进行调整;

max（νni）-νni是将所有DMU置于同质条件下。

1.3 第三阶段：调整投入要素后的BCC-DEA建模

在此阶段，调整投入要素（剔除环境变量

和随机因素），再次运用BCC-DEA模型，可得出同质条件下的真实效率值[13]。本文采用的运算工具为DEAP 2.1和Frontier 4.1软件。

2 评价指标选取

2.1 投入和产出指标

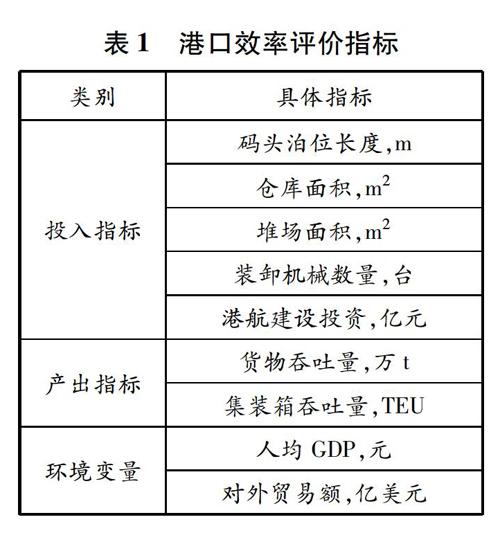
本文在选取投入指标时，重点考虑资源（包括岸线和土地资源）、设施设备和建设投资等3类要素，同时结合数据可得性、可比性及指标合理性。具体投入指标包括码头泊位长度、仓库面积、堆场面积、装卸机械数量和港航建设投资。产出指标包括货物吞吐量和集装箱吞吐量。

2.2 环境变量

从世界港口发展历程看，除港口投入和产出指标直接影响港口效率外，地区对外贸易、经济发展水平、宏观政策等外部环境也在一定程度上影响港口效率。基于此，本文主要考虑以下两个因素作为环境变量：（1）人均地区生产总值（人均GDP），综合反映某地区经济发展水平，既衍生了港口生产需求，又影响港口建设、投资规模等;（2）对外贸易额，主要反映贸易活动对港口的需求，在相同的投入水平下航运需求会随对外贸易额的增加而增加。

综上，港口效率评价指标见表1。

3 实证分析

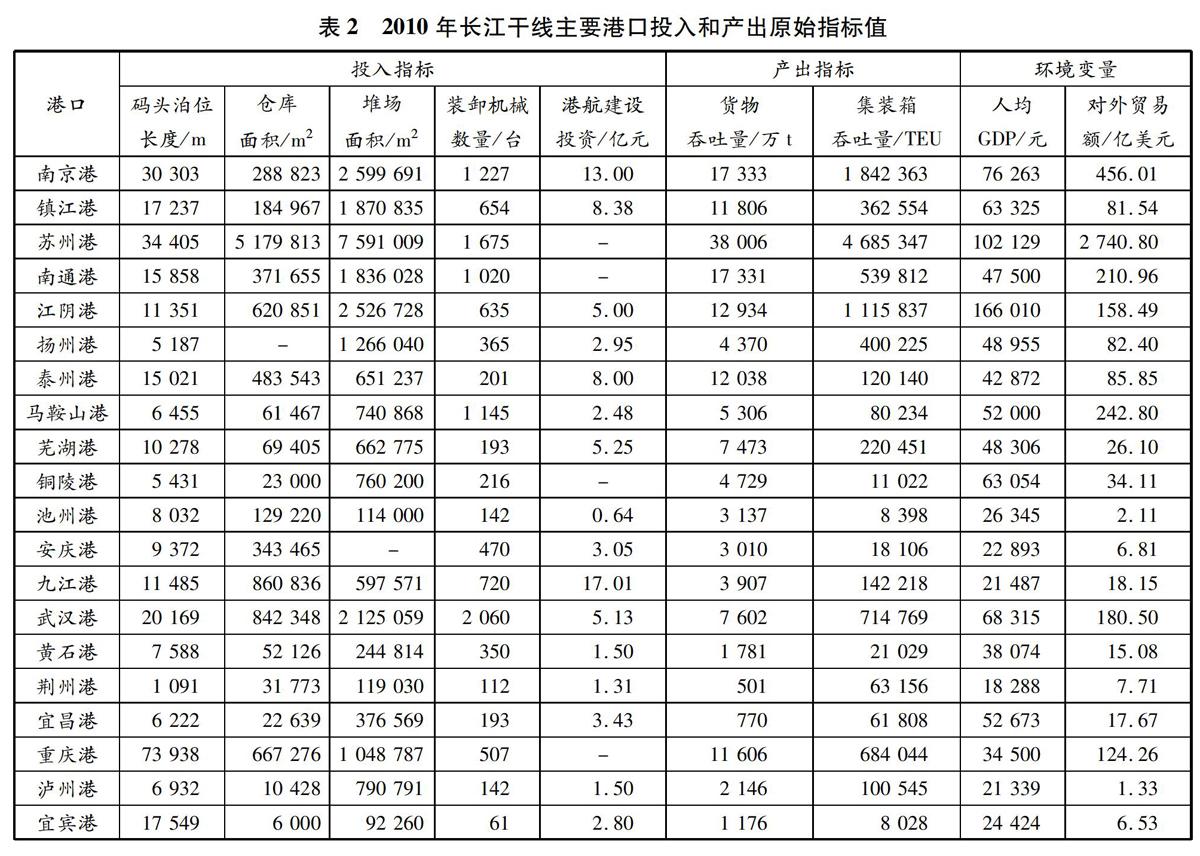
以长江干线20个主要港口为研究样本，包括上游港口（宜昌港、重庆港、泸州港和宜宾港）、中游港口（武汉港、黄石港、荆州港、九江港）和下游港口（南京港、镇江港、苏州港、南通港、江阴港、扬州港、泰州港、马鞍山港、芜湖港、铜陵港、池州港、安庆港）。文中港口投入和产出指标主要来源于2010年和2017年《全国交通运输统计资料汇编》，其中港航建设投资数据来源于《中国港口年鉴》，环境变量指标来源于《中国城市统计年鉴》和各港口城市的《国民经济和社会发展统计公报》。投入和产出原始指标值见表2和3。

3.1 传统DEA效率评价结果

运用DEAP 2.1对比分析2010年、2017年长江干线20个主要港口的效率水平与规模报酬，见表4。结果表明：在不考虑环境变量和随机因素的情况下2010年长江干线港口的平均综合效率为0.685，平均纯技术效率和规模效率分别为0.877和 0.772;2017年平均综合效率0.887，平均纯技术效率和规模效率均为0.941;总体上长江干线港口的整体效率较高，且2017年港口效率水平比2010年的有显著提升。

（1）长江干线各港口效率差距明显。2010年，镇江港、马鞍山港、九江港、黄石港、宜昌港和宜宾港的综合效率均不足0.5，明显低于港口综合效率均值。到2017年，上述几个港口综合效率明显提升，其中镇江港、黄石港、宜昌港和宜宾港综合效率为1，达到效率前沿面，马鞍山港和九江港的综合效率也超过0.8。然而，南通港、扬州港、荆州港和重庆港2017年的综合效率相较于2010年的明显降低，除重庆港外的其他3个港口的纯技术效率均为1，说明规模效率低下是导致综合效率水平降低的主要原因，也说明这3个港口本身并不存在投入冗余和产出不足的问题，其效率低是因为规模与投入产出不匹配。因此，在港口发展过程中需要进一步优化港口规模，以达到较高的经济效益。相较于2010年，2017年重庆港除了规模效率下降外，纯技术效率也有所降低，其综合效率未能达到有效前沿，主要原因是重庆港规模效率低下，投入冗余，产出不足，此时应根据各港口发展实际情况，进一步优化资源配置，从改善码头基础设施、完善集疏运体系等方面提高港口运营效率。

（2）从规模报酬看，2010年多数港口规模报酬递增，即增加其投入能带来更高效的产出，而规模报酬不变的港口则达到了效率前沿面，意味着同比例增加各类投入能带来相同比例的产出增加。到2017年，南通港、九江港和重庆港规模报酬递减，而达到效率前沿面的港口增加了镇江港、泰州港、芜湖港、黄石港、宜昌港、泸州港和宜宾港。2017年未达到效率前沿面的港口中，除池州港外，其他港口的技术效率均低于其综合效率，即效率水平低下的主要原因是技术低效，但不能排除客观环境和随机因素的影响。

（3）从效率动因看，多数港口普遍存在规模效率低于纯技术效率的现象，主要原因是：港口是规模效应显著的重点领域，在港口建设初期基础设施投资相对分散，且港口与上下游企业还未实现有效融合发展，难以形成规模效应;纯技术效率受区域经济及对外贸易迅速发展的影响，港口货物吞吐量不断增长，在既定的港口资源投入上可获得高效回报。

3.2 环境变量對港口效率的影响

运用Frontier 4.1将第一阶段DEA模型结果中5个投入变量的松弛值作为被解释变量，将人均GDP、对外贸易额两个环境变量作为解释变量，构建SFA回归模型[13]，结果见表5。

由表5可以看出，港口城市的人均GDP和对外贸易额均在至少10%的显著水平下通过了检验，说明上述两个环境变量能够显著影响港口效率，即随着港口城市经济发展和对外贸易水平的提升，港口经济实现快速发展，有利于提高港口的投入产出比。

（1）人均GDP。人均GDP与码头泊位长度、仓库面积和装卸机械数量为负相关关系，主要原因在

于：随着人均GDP的增长，港口投入大幅增加，但港口货物吞吐量未能实现同比例增长，导致港口投入产出比降低。人均GDP与堆场面积松弛变量正相关，可能是因为人均GDP增加会带来货物吞吐量的增长，从而提高港口资源利用率。此外，人均GDP对港航建设投资的影响不明显。

（2）对外贸易额。对外贸易额与码头泊位长度、港航建设投资为正相关关系。对外贸易额的增长可能带来港口吞吐量的增加，从而推动码头、航道等基础设施建设，进一步提升港口的投入产出比。该指标与仓库面积、堆场面积和装卸机械数量为互相关关系，可能是由于对外贸易额

的增长带来港口建设投资的增加，但产出并未相应

增长，导致港口资源利用率较低。

上述分析结果表明环境变量和随机因素在很大程度上影响了长江干线主要港口效率，进行港口效率评价时必须剔除环境变量和随机因素的影响。因此，根据此阶段的回归结果，重新调整港口投入变量，同时保持原有的产出变量不变，再次构建传统DEA-BBC模型，求得各港口的真实效率值。

3.3 同质环境下的港口效率分析

利用剔除环境变量和随机因素的影响后的投入变量，运用BCC-

DEA模型分析2010年、2017年长江干线主要港口效率，得出各港口的最终效率值，见表6。由表6可以看出：

（1）镇江港。2010年，镇江港规模报酬递减，其规模效率和纯技术效率均未达到最优。到2017年，镇江港规模报酬不变，综合效率达到最优前沿面。这表明经过几年的建设发展，镇江港的码头岸线、装卸机械和建设投资等要素的投入结构进一步优化，港口产出效率提升，综合效率达到最优值。

（2）重庆港、扬州港。这两个港口均从2010年的规模报酬不变转为2017年的规模报酬递增，其中：扬州港主要是规模效率降低，即港口要素投入增加后并未带来相应的产出增加，因此需要加快调整要素投入结构和规模，改善港口经营效率;重庆港则是纯技术效率明显降低，可能是由于随着港口要素投入和作业能力的不断提升，港口在信息处理、运营管理等方面未能实现同步提升，导致综合效率降低。

（3）池州港、安庆港、荆州港。这3个港口均表现为规模报酬递增，但规模效率明显降低导致2017年港口综合效率下降，说明这3个港口在码头岸线、土地资源、装卸机械、建设投资等要素方面存在投入不足且结构不合理的情况。因此，这3个港口应根据实际情况，一方面调整各类生产要素的结构，使各项要素比例更加协调，另一方面应加大投入规模，进

一步提升港口经营效率。

3.4 两种环境条件下的效率对比分析

对比分析第三阶段和第一阶段的DEA结果，即对比表4和6，可以看出剔除环境变量和随机因素的影响后，DMU效率表现出显著差异。

（1）平均效率比较分析。环境变量和随机因素在很大程度上影响了港口效率水平，在剔除环境变量和随机因素的影响后2010年长江干线20个主要港口的综合效率、纯技术效率总体上呈现上升趋势，但规模效率呈下降趋势;而2017年各港口综合效率、规模效率均呈现下降趋势，纯技术效率呈现上升趋势。这说明港口投入结构与规模不匹配，需根据不同港口规模报酬的增减情况优化港口规模，进一步提升港口效率。在剔除环境变量和随机因素的影响后，2017年各港口的平均效率比2010年的反而降低，更说明需要重视投入结构和规模经济效应。

（2）纯技术效率比较分析。2010年和2017年，除达到效率前沿面的港口外，在剔除环境变量和随机因素的影响后所有港口纯技术效率均明显提升，表明近几年港口投入与产出水平的匹配度明显提升，所有港口的投入结构优化产生了更大的产出效益。

（3）规模效率比较分析。在剔除环境变量和随机因素的影响后2010年20个港口中位于长江中上游的大部分港口（包括安庆港、九江港、武汉港、荆州港、宜昌港和泸州港）规模效率降低;而2017年，除南通港的规模效率提升外，其他港口的规模效率下降，说明在同质环境下，规模与产出不相匹，需要优化港口规模，使之符合各港口发展实际。

4 结 论

本文运用三阶段DEA模型对比分析了2010年、2017年长江干线20个主要港口的经济效率，结果表明：（1）长江干线各主要港口，特别是长江中上游港口的规模效率相对较低，尚未形成规模效应;（2）长江干线大部分港口纯技术效率达到最优，仍有部分港口存在投入拥挤和产出水平低的现实情况，港口资源浪费比较严重;（3）在不考虑环境因素影响的情况下，与2010年相比，2017年长江干线主要港口的平均效率明显提升，但在同质条件下2017年港口效率反而下降，说明环境变量和随机因素对港口效率有重大影响，需要科学把握和调整外部环境变量从而提升港口经济效率。

参考文献：

[1]DE OLIVEIRA G F， CARIOU P. The impact of competition on container port （in）efficiency[J]. Transportation Research Part A， 2015， 78： 124-133.

[2]KUTIN N， NGUYEN T T， VALLE T. Relative efficiencies of ASEAN container ports based on data envelopment analysis[J]. The Asian Journal of Shipping and Logistics， 2017， 32（2）： 66-67.

[3]YUEN A C， ZHANG Anming， CHEUNG Waiman. Foreign participation and competition： a way to improve the container port efficiency in China？[J]. Transportation Research Part A， 2013， 49： 220-231.

[4]龐瑞芝. 我国主要沿海港口的动态效率评价[J]. 经济研究， 2006（6）： 92-100.

[5]匡海波， 陈树文. 中国港口生产效率研究与实证[J]. 科研管理， 2007（5）： 170-176.

[6]沈金生， 郁威. 环渤海地区主要港口经济效率研究[J]. 华东经济管理， 2014， 28（10）： 72-76. DOI： 10.3969/j.issn.1007-5097.2014.10.014.

[7]王玲， 孟辉. 我国内河港口与沿海港口的效率对比： 基于共同边界和序列SBM-DEA的研究[J]. 软科学， 2013， 27（3）： 90-95.

[8]王玲， 毕志雯. 基于三阶段DEA模型的我国主要内河港口效率研究[J]. 产业经济研究， 2010（4）： 40-48. DOI： 10.13269/j.cnki.ier.2010.04.006.

[9]赖成寿， 吕靖， 李祥全. 基于二阶段DEA博弈交叉效率模型的港口生产效率研究[J]. 上海海事大学学报， 2018， 39（1）： 52-59. DOI： 10.13340/j.jsmu.2018 01.010.

[10]CHARNES A， COOPER W W， RHODES E. Measuring the efficiency of decision making units[J]. European Journal of Operational Research， 1978， 2： 429-444. DOI： 10.1016/0377-2217（78）90138-8.

[11]FRIED H O， LOVELL C A K， SCHMIDT S S， et al. Accounting for environmental effects and statistical noise in data envelopment analysis[J]. Journal of Productivity Analysis， 2002， 17： 157-174. DOI： 10.1023/a：1013548723393.

[12]杨健， 徐佳胤. 基于DEA模型的港口物流生产效率评价研究[J]. 三峡大学学报（自然科学版）， 2017， 39（2）： 19-23. DOI： 10. 13393/j.cnki， issn.1672-948X.2017.02.005.

[13]李璐， 朱洪兴， 单奎. 基于SFA模型和Mulmquist指数的河南省区域技术创新效率分析[J]. 科技管理研究， 2014（9）： 49-54. DOI： 10. 3969/ j. issn.1000-7695.2014.09.011.

（编辑 贾裙平）

收稿日期： 2019-09-03

修回日期： 2019-11-27

基金项目： 国家社会科学基金（14ZDB131）

作者简介：

杜利楠（1986—），女，河北廊坊人，副研究员，研究方向为交通运输规划与管理、港口经济，（E-mail）dulinan@wti.ac.cn