具有横倾抑制功能的船舶PID微分补偿航向控制
2020-10-20孙武臣卜仁祥刘勇
孙武臣 卜仁祥 刘勇
摘要:为改善船舶航向自动舵性能和减小船舶转向时的横倾幅度,提出一种基于模糊逻辑控制和滑模PID微分补偿的船舶航向保持控制策略。分析PID控制的积分超调问题和船舶转向时的横倾特点。对PID控制进行滑模变形,并引入微分项对PID控制的积分项进行补偿以消除积分超调。以横倾角和横倾角速度为输入设计模糊控制规则,对滑模PID微分补偿控制器参数进行调节以减小转向时横倾角。以集装箱船“MV KOTA SEGAR”MMG模型为控制对象进行MATLAB仿真。仿真结果表明:该控制器能够减小船舶转向时的横倾幅度,最大横倾抑制率可达71%;解决了PID控制的积分超调问题,具有参数易调节等特点。
关键词:航向保持控制; 横倾抑制; PID微分补偿; 模糊逻辑控制
中图分类号: U664.82
文献标志码:A
Ship course control with heel inhibition capacity
based on PID differential compensation
SUN Wuchen, BU Renxiang, LIU Yong
(Navigation College, Dalian Maritime University, Dalian 116026, Liaoning, China)
Abstract:
In order to improve the ship course autopilot performance and reduce the heel amplitude during ship steering, a ship course keeping control strategy based on the fuzzy logic control and the sliding mode PID differential compensation is proposed. The integral overshoot problem of PID control and the heel feature when ship steering are analyzed. PID control is deformed by the sliding mode, and the differential term is introduced to compensate the integral term of PID control to eliminate the integral overshoot. A fuzzy control rule is designed with the heel angle and the angular velocity of heel as the input, and the parameters of the sliding mode PID differential compensation controller are adjusted to reduce the heel angle during ship steering. The MMG model of the container ship “MV KOTA SEGAR” is used as the control object for MATLAB simulation. The simulation results show that: the controller can reduce the heel amplitude during ship steering, and the maximum heel inhibition rate can reach 71%; the integral overshoot problem of PID control is solved, and the parameters are easy to adjust.
Key words:
course keeping control; heel inhibition; PID differential compensation; fuzzy logic control
0 引 言
自20世紀20年代初陀螺罗经研制工作取得实质性进展后,船舶航向保持控制一直是船舶运动控制领域的重要研究课题[1]。最初的航向控制器只是简单的比例控制,且只能用于低精度要求的航向保持控制,但它让人们看到了在船舶操纵领域实现自动控制的希望。后来随着伺服系统理论和电子器件的发展,出现了PID自动舵。PID自动舵具有结构简单可靠、控制参数少等优点,因此目前大多数船舶仍装备这种舵。由于PID自动舵的设计基于精确数学模型,而船舶运动模型随速度、水深、载荷状态和外部环境干扰的变化而变化,所以常规PID自动舵很难保证在所有的情况下都具有满意的控制效果[2]。为解决上述问题,在20世纪60年代末瑞典等国家的学者将自适应技术应用于船舶航向保持控制,提高了自动舵在各种气候条件下适用的可能性[3-4]。然而自适应方法以参数估算或模型试验为基础,建立精确的船舶运动数学模型是困难的,只有经验丰富的舵手才能很好地控制船舶。自20世纪80年代以来,人们开始寻求类似于人工转向的智能控制技术,各种新型控制算法被应用于航向自动舵,如:TZENG[5]将船舶转向过程控制转化为采用顺序梯度恢复算法(sequential gradient-restoration algorithm)解决的BOLZA最优控制问题,实现了从设定航向到期望航向的平稳过渡,并可在航向响应速度与超调量之间进行权衡;刘胜等[6]运用饱和局部分析法,将不确定非线性船舶动力模型转化为线性微分包含模型,设计了饱和线性反馈控制律,设计的控制器具有工程实现容易、转向平稳快速和无超调等特点;张显库等[7]利用闭环增益成形算法设计对模型摄动和风浪干扰具有一定鲁棒性的PID控制器,改进了设计分区前馈控制器,提高了转向时的响应速度、系统灵敏度和系统控制质量;甘浪雄等[8]设计了航向成形算法对船舶转向过程进行前馈调节,并改进模糊PID控制器,提高了控制的动态性能和稳态精度等。
然而,现有的航向控制器主要针对航向保持和转向过程进行控制,很少考虑船舶转向过程中的横倾问题。船舶转向尤其大角度转向必然产生横倾,过度的横倾不仅严重威胁船舶航行安全,而且对船舶适航性、货物绑扎固定、船员舒适性有很大的影响[9],对滚装船、客滚船、集装箱船、豪华邮轮等重心较高的船舶的影响更甚。
本文针对传统PID控制参数不易调节、积分超调问题,对传统PID控制进行滑模变形,不再是单独对航向偏差积分,而是对航向偏差和偏差变化率同时积分;为减小船舶转向时的横倾幅度,根据船舶转向时横倾角大小及其变化率,设计模糊控制规则,对控制器参数进行调节。利用MATLAB仿真环境进行验证,建立了集装箱船“MV KOTA SEGAR”MMG模型并加入了風干扰和舵机模型,以更接近实际情况。
1 基本描述
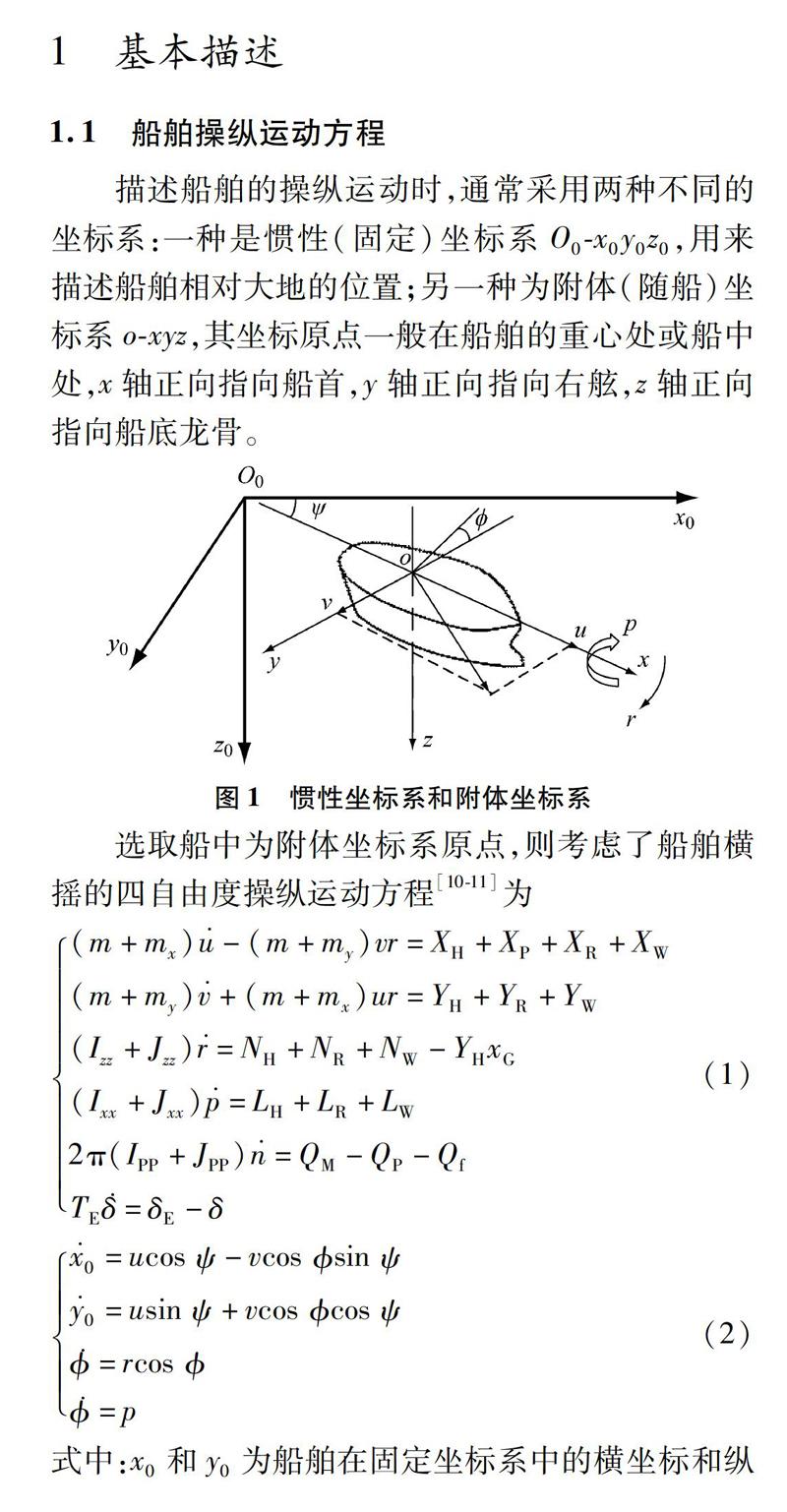
1.1 船舶操纵运动方程
描述船舶的操纵运动时,通常采用两种不同的坐标系:一种是惯性(固定)坐
标系O0-x0y0z0,用来描述船舶相对大地的位置;另一种为附体(随船)坐标系o-xyz,其坐标原点一般在船舶的重心处或船中处,x轴正向指向船首,y轴正向指向右舷,z轴正向指向船底龙骨。
选取船中为附体坐标系原点,则考虑了船舶横摇的四自由度操纵运动方程[10-11]为
式中:x0和y0为船舶在固定坐标系中的横坐标和纵坐标;u和v分别为船舶在附体坐标系中的纵向速度和横向速度;ψ和r分别为艏向角和转艏角速度;和p分别为横倾角和横倾角速度;n、δE和δ分别为主机转速、命令舵角和实际舵角;TE为舵机时间常数,一般取2.5~3 s;m、mx和my分别为船舶的质量、纵向附加质量和横向附加质量;Izz和Jzz分别为船舶的转动惯量和附加转动惯量;X和Y分别为作用于船体纵向和横向的力;N和L分别为绕垂直轴和纵轴的力矩;下标H、P、R和W分别表示流体黏性、螺旋桨、舵叶和外界干扰;xG为船舶重心在附体坐标系中x方向上的坐标;Ixx和Jxx分别为船舶的横摇惯性矩和附加转动惯量;IPP和JPP分别为螺旋桨与轴系的转动惯量和附加转动惯量;QM、QP和Qf分别为主机产生的转矩、螺旋桨吸收的转矩和轴系摩擦消耗的转矩。
1.2 控制目标
控制目标为确定舵角δ,使船舶保持期望航向航行,即航向偏差ψe→0,且转向时船舶具有横倾抑制功能。
2 控制器设计
2.1 PID微分补偿控制设计
PID控制率的基本形式为
由于PID控制器的3个参
数kp、ki和kd之间相互影响,调整其中一个参数,可能会影响另外两个参数的性能,所以对式(3)的形式稍作变形,可得到
观察式(5)可知,PID控制的3个参数转化为k1、k2和kd,参数的物理意义变得更为明显,有利于参数的调节和优化[12-13]。为方便书写,kd用k3代替。
为消除积分超调问题,在式(5)的积分项中添加微分项进行补偿,可得
由式(7)可知,控制器的参数仍为3个,但在系统输出趋近于稳定(即ψe>0,而e<0;或ψe<0,而e>0)时能够抵消积分项对系统输出偏差的积分,而在系统偏差偏离控制目标(即ψe<0,而e<0;或ψe>0,而e>0)时积分项会加速系统稳定。
2.2 模糊横倾抑制设计
根据船舶转向时横倾变化特点[14-15],以横倾
角和横倾角速度p为输入,Δk3为输出设计模糊控制规则,对PID微分补偿控制器参数进行调节以达到抑制横倾的目的。
对横倾角、横倾角速度p和输出Δk3的模糊集和论域定义如下:、p和Δk3的模糊集均取为{NB, NM, NS, ZO, PS, PM, PB},其中NB、NM、NS、ZO、PS、PM和PB分别表示负大、负中、负小、零、正小、正中和正大;的论域为{-6, -5, -4, 0, 4, 5, 6};p的论域为{-0.5, -0.4, -0.3, 0, 0.3, 0.4, 0.5};Δk3的论域为{-18, -12, -6, 0, 6, 12, 18}。论域可根据需要自行设计,上面的数
据是以“MV KOTA SEGAR”MMG模型为被控对象设计的。隶属度函数选用三角形隶属度函数和S形隶属度函数。通过仿真,由横倾角和横倾角速度p变化趋势设计减小横倾的模糊控制规则,根据49条模糊规则(见表1)建立模糊控制表。系统的输入、输出隶属度函数见图2~4。数值计算采用MAMDANI的Min模糊蕴含关系[16]、ZADEH的Max-min推理合成、最大隶属度平均法(mom)去模糊化[17]等算法。
2.3 控制器工作原理示意图
具有横倾抑制功能的PID微分补偿控制器工作原理示意图见图5。
3 仿真验证与分析
为验证控制策略的可行性和控制效果,本文以集装箱船“MV KOTA SEGAR”为仿真对象,对不同情况下的横倾和航向变化进行仿真和对比分析。船型主要参数:垂线间长217 m;型宽37.3 m;型深15.693 m;吃水12.5 m;排水量67 867.2 t;螺旋桨直径7.9 m;舵叶面积48.8 m2。控制器参数:k1=0.004 6;k2=0.028; k3=18;k=0.033。
3.1 仿真1
设定初始航速19.4 kn、风向30°、风速10 m/s,恒定风的影响用风压差角表示[18],浪和随机风的影响采用白噪声驱动的二阶振荡环节H(s)=0.419 8s/(s2+0.363 8s+0.367 5)表示[19-20],初始航向偏差为60°,PID微分补偿控制器与常规PID控制器结果对比见图6。
由图6可知,常规PID控制器下航向曲线存在4°左右超调。产生超调的根本原因是积分项的存在:在航向趋于稳定的过程中,积分项积累了不利信息(A区),而在航向偏差偏离目标时积分反应又过于迟钝;根据积分性质,必然产生反向积分区域(B区),而且只有B区面积等于A区面积,才能使航向偏差最终趋于零。PID微分补偿控制器下的航向曲线不存在超调,且航向稳定时间比常规PID控制器下的明显缩短,这是由于控制器中的微分补偿项在航向趋于稳定的过程中抵消了积分项对偏差的积分,而在航向偏离目标时加快了积分项的反应速度,抑制航向继续偏离目标,从而加快系统稳定。
3.2 仿真2
在船舶转向操纵过程中,由于艏摇与横摇之间相互耦合,所以横倾不可避免。小横倾角对船舶航行安全影响不大,但过大的横倾角严重威胁船舶航行安全,甚至会导致船舶倾覆。因此,设计的控制器应该对小横倾角不敏感,对越大的横倾角,横倾抑制能力越强。利用不同初稳心高度(GM)条件下船舶转向时横倾角不同,设计仿真实验对控制器这种性能进行验证。设定GM分别为0.6 m、0.9 m,初始航向偏差为60°,横倾抑制效果分别见图7和8。由图7和8可知:当GM为0.6 m时,在横倾抑制作用下最大横倾角由9.5°减为3.3°,横倾抑制率为65%;当GM为0.9 m时,在横倾抑制作用下最大横倾角由6.3°减为3.2°,横倾抑制率为49%。GM为0.6 m时的横倾抑制效果明显优于GM为0.9 m时的横倾抑制效果,验证了该控制器横倾角越大,横倾抑制效果越好的特点。
3.3 仿真3
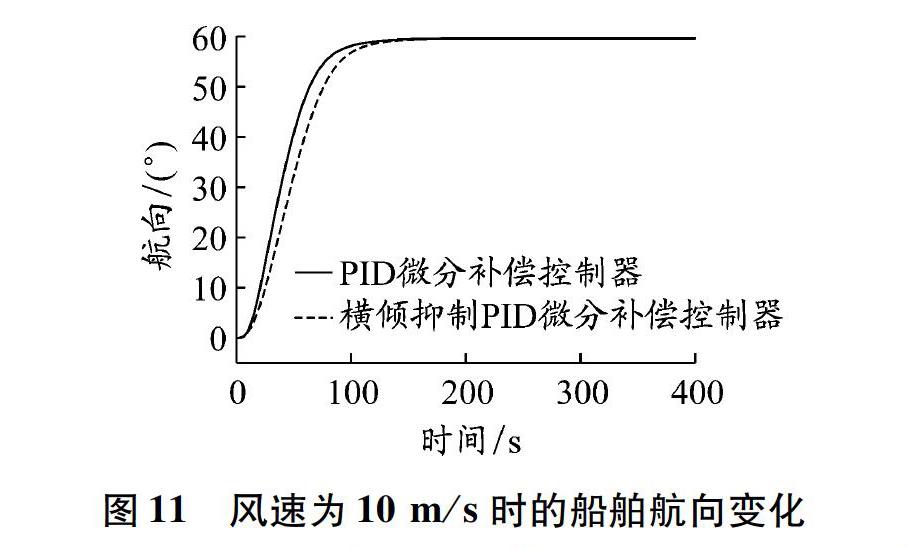
设定风速分别为10 m/s和18 m/s,其他干扰条件同仿真1,GM为 0.6 m,初始航向偏差为60°。不同风速条件下的横倾抑制效果见图9和10,风速为10 m/s时的船舶航向变化见图11。
由图9和10可知:当风速为10 m/s时,最大横倾角在横倾抑制作用下由13.4°减为5.6°,横倾抑制率为58%;当风速为18 m/s时,最大横倾角在横倾抑制作用下由20.8°减为10.9°,横倾抑制率为48%。与图7对比可知,风干扰使船舶转向时横倾角增大,且航向保持时船舶具有稳定横倾,可见该控制器对稳定横倾不起作用,这是因为:用于横倾抑制功能的模糊控制规则是以横倾角和横倾角速度为输入而设计的,当船舶处于稳定横倾状态时,横倾角速度为零,按照模糊控制规则此时对应的输出为零,对PID微分补偿控制器参数没有影响,即此时控制器不具有横倾抑制功能。这种设计符合航海实际情况,船舶在风力作用下所产生的稳定横倾不宜通过舵角来调整,因为用舵角调整不仅会增加舵机燃油消耗,而且会给控制器的航向保持功能带来不确定影响。实船上一般通过压载水系统调节稳定横倾,这不是本文研究内容,暂不详细介绍。由图11可以看出,在具有横倾抑制功能的PID微分补偿控制器作用下的航向响应速度略慢,因此在设计具有横倾抑制功能的控制器时需充分考虑实际情况,避免因不必要的加强横倾抑制功能而减慢航向响应速度。
3.4 仿真4
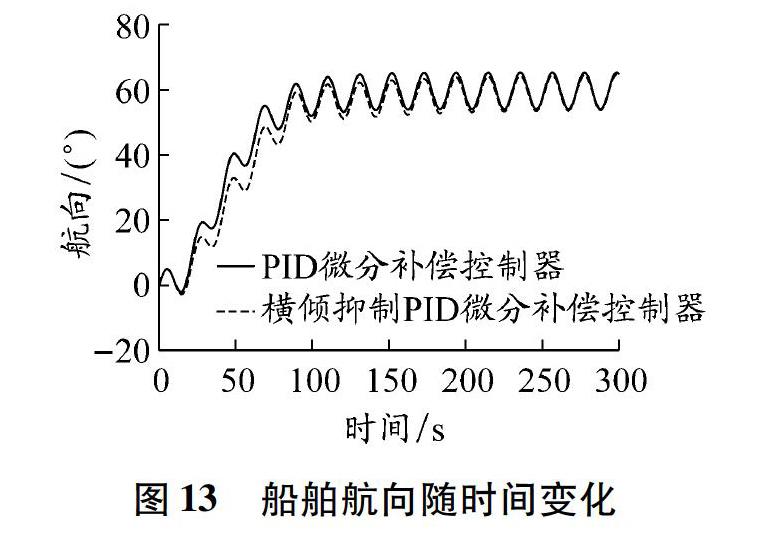
设计具有横倾抑制功能的控制器的目的是为了减小船舶转向时的横倾幅度,同时不影响船舶的航向保持功能。为验证控制器的这种性能,设定GM为0.6 m,初始航向偏差为60°,船首向受幅值为5°的正弦信号干扰进行仿真。其横倾抑制效果见图12,船舶航向变化见图13。
观察仿真结果可知:(1)在船舶转向开始时,控制器具有很好的横倾抑制效果,最大横倾抑制率可达71%;与PID微分补偿控制器相比,在横倾抑制PID微分补偿控制器下船舶航向响应速度略慢,再次验证了仿真图10得到的结论。(2)在船舶进入航向保持阶段后,在正弦信号干扰下,横倾抑制PID微分补偿控制器能够很好地跟踪控制目标,且具有一定的横倾抑制功能。仿真结果验证了该控制器能够减小船舶转向时的横倾幅度,防止转向时横倾过大,控制器的横倾抑制功能不会影响船舶的航向保持功能,实现了控制器设计的目的。
4 结 论
本文对船舶航向PID控制率进行了滑模变形,并引入了微分项对PID控制中的积分项进行补偿;根据船舶转向时的横倾特点设计了模糊逻辑规则,用以调节PID微分補偿控制器的参数,使控制器能够减小船舶转向时的横倾幅度,具有横倾抑制功能。采用集装箱船“MV KOTA SEGAR”MMG模型进行仿真,结果验证了本文所设计的控制器能够消除常规PID控制器的积分超调问题,在船舶转向时具有横倾抑制功能,横倾角越大横倾抑制效果越好,最大横倾抑制率可达71%,且不影响船舶航向保持性能,符合航海实际需求。为提高控制器的鲁棒性,下一步的工作是将控制器与其它智能控制技术相结合,对控制器参数进行在线优化。
参考文献:
[1]徐国平, 张显库. 船舶自动舵研究综述[J]. 中国造船, 2013, 54(2): 191-200.
[2]张显库. 船舶控制系统[M]. 大连: 大连海事大学出版社, 2010: 4-7.
[3]贾欣乐, 张显库. 船舶运动智能控制与H∞鲁棒控制[M]. 大连: 大连海事大学出版社, 2002: 9-13.
[4]HASELTALAB A, NEGENBORN R R. Adaptive control for autonomous ships with uncertain model and unknown propeller dynamics[J]. Control Engineering Practice, 2019, 91: 1-12.
[5]TZENG C Y. Optimal control of a ship for a course-changing maneuver[J]. Journal of Optimization Theory and Applications, 1998, 97: 281-297. DOI: 10.1023/A:1022674516570.
[6]刘胜, 周丽明. 船舶转向静态饱和控制器设计[J]. 系统仿真学报, 2009, 21(7): 1983-1985. DOI: 10.16182/j.cnki.joss.2009.07.072.
[7]张显库, 赵翔宇. 船舶转向的鲁棒控制及其优化设计[J]. 哈尔滨工程大学学报, 2006, 27(3): 319-322.
[8]甘浪雄, 邓巍, 周春辉, 等. 船舶航向模糊控制器优化设计及仿真[J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(3): 398-403. DOI: 10.3963/j.issn.2095-3844.2019.03.005.
[9]LIANG Lihua, WEN Yu. Rudder roll stabilization with disturbance compensation model predictive control[J]. Journal of Marine Science and Technology, 2019, 24: 249-259. DOI: 10.1007/s00773-018-0550-6.
[10]贾欣乐, 杨盐生. 船舶运动数学模型: 机理建模与辨识建模[M]. 大连: 大连海事大学出版社, 1999: 170-173.
[11]YO Fukui, HIROTAKE Yokota, HIROYUKI Yano, et al. 4-DOF mathematical model for manoeuvring simulation including roll motion[J]. Journal of Marine Science and Technology, 2016, 24: 167-179. DOI: 10.2534/jjasnaoe.24.167.
[12]卜仁祥. 欠驱动水面船舶非线性反馈控制研究[D]. 大连: 大连海事大学, 2007.
[13]朱业求. 船舶航向PID控制参数优化研究[D]. 大连: 大连海事大学, 2012.
[14]HIRANO M, TAKASHINA J. A calculation of ship turning motion taking coupling effect due to heel into consideration[J]. Transactions of the West-Japan Society of Naval Architects, 1980, 59: 71-81.
[15]王立军. 船舶大舵角转向时艏摇与横摇的耦合仿真研究[J]. 船舶与海洋工程, 2013(1): 6-11.
[16]MAMDANI E H, ASSILIAN S. An experiment in linguistic synthesis with a fuzzy controller[J]. Internatinal Journal of Man-Machine Studies, 1975, 7(1): 1-13. DOI: 10.1016/S0020-7373(75)80002-2.
[17]ZADEH L A. Fuzzy sets[J]. Journal of Information and Control, 1965, 8: 338-353. DOI: 10.1016/S0019-9958(65)90241-X.
[18]SUN Wuchen, BU Renxiang, LIU Yong, et al. Prediction of leeway and drift angle based on empirical formula[C]//2018 Asia-Pacific Conference on Intelligent Medical and 7th Internaltional Conference on Trasportation and Traffic Engineering (APCIM 2018 & ICTTE 2018). Association for Computing Machinery, 2018: 196-199. DOI: 10.1145/3321619.3321661.
[19]ZHANG Xianku, FENG Yongxiao. Control algorithm of YUPENG ship autopilot based on tangent function nonlinear feedback[J]. Journal of Measurement Science and Instrumentation, 2017, 8(1): 73-78. DOI: 10.3969/j.issn.1674-8042.2017.01.012.
[20]馮永孝, 张显库. 非线性修饰与模糊控制船舶航向保持控制比较[J]. 中国航海, 2018, 41(4): 12-15, 27.
(编辑 贾裙平)
收稿日期: 2019-11-27
修回日期: 2020-01-03
基金项目:
国家自然科学基金(61751202, 61751205, U1813203);辽宁省自然科学基金引导计划(20170540089);辽宁省自然科学基金计划重点项目(20170540098);大连海事大学航海学院2019年一流学科开放研究基金
作者简介:
孙武臣(1987—),男,河南鹿邑人,硕士研究生,研究方向为船舶运动控制、航海科学与技术,(E-mail)chenwusun@163.com;
卜仁祥(1975—),男,辽宁岫岩人,副教授,博士,研究方向为交通运输工程、船舶运动控制、航海科学与技术,(E-mail)burenxiang@dlmu.edu.cn
