基于迭代滑模的船舶动力定位非线性控制

陈海力　任鸿翔　杨柏丞　衣莹

摘要：针对存在外界干扰的船舶动力定位控制问题，提出一种简捷的迭代滑模控制算法。选择迭代滑模面，并将其与反步法结合，设计迭代滑模控制律。采用Lyapunov理论对系统的稳定性进行证明。将提出的控制算法与PID控制算法和传统反步滑模控制算法进行理论分析比较和仿真结果比较，结果表明迭代滑模控制算法具有超调小，收敛速度快，稳定性和鲁棒性好的优点。

关键词：迭代滑模; Lyapunov理论; 积分补偿; 动力定位控制; 反步法

中图分类号：  U664.82

文献标志码：A

Ship dynamic positioning nonlinear control based on

iterative sliding mode

CHEN Haili1， REN Hongxiang1， YANG Baicheng1， YI Ying2

（1. Navigation College， Dalian Maritime University， Dalian 116026， Liaoning， China;

2. Offshore Enforcement Fleet， Dalian Agriculture and Countryside Development Service Center， Dalian 116113， Liaoning， China）

Abstract：

For the dynamic positioning control issue of ships with external interference， a simple iterative sliding mode control algorithm is proposed. The iterative sliding mode surface is selected and combined with the backstepping technique to design the iterative sliding mode control law. Lyapunov theory is used to prove the stability of the system. Through the comparison of theoretical analysis and simulation results of the proposed control algorithm， the PID control algorithm and the traditional backstepping sliding mode control algorithm， it is shown that the iterative sliding mode control algorithm is of the advantages of small overshoot， fast convergence， good stability and robustness.

Key words：

iterative sliding mode; Lyapunov theory; integral compensation; dynamic positioning control; backstepping technique

0 引 言

當今船舶动力定位控制方法层出不穷，典型的包括PID控制算法、反步（backstepping）控制算法、滑模控制算法、模型预测控制算法等。PID控制算法最早被成功应用到动力定位控制中。然而，该方法鲁棒性差，且控制律中的积分项会导致系统有较大的超调量[1]。文献[2-3]利用神经网络和模糊方法对控制器参数进行了整定，使得系统超调量减小，仿真效果更好。文献[4]将反步控制算法应用到船舶动力定位控制中，针对模型中的不确定项和外界干扰采用神经网络进行自适应逼近，最后用Lyapunov理论进行了稳定性证明。该方法的缺点是控制器参数不具有明确的意义，参数的选取主要依靠试凑法。文献[5]将基于线性矩阵不等式的滑模控制算法应用到船舶动力定位控制中，通过设计矩阵不等式求解状态反馈增益，采用饱和函数代替符号函数消除了抖动。仿真结果表明，与基本滑模控制算法相比，该算法保证船舶在横向、纵向和艏向上的收敛速度都有极大提高。然而，虽然采用饱和函数消除了抖动，但却牺牲了系统的稳定性。文献[6]提出利用积分方法逼近外界干扰的上界。该方法不仅解决了滑模控制算法的抖动问题，而且很好地解决了由采用饱和函数引起的稳态误差变大的问题。文献[7]第一次提出迭代滑模控制算法，它首先对低阶变量设计滑动模态，对进入滑动模态前的正常运动的趋近控制使用迭代滑模控制方法。该方法具有控制器设计简单、灵活的优点，并且参数的选取更具有实际意义，即参数可以根据控制要求进行设计。该算法自提出以来，在欠驱动船舶航向控制[8-10]、航迹控制[11-12]、水下机器人控制[13]等领域得到了很好的研究应用。然而，迭代滑模控制算法的稳定性证明是一个难题。

基于上述研究现状，将迭代滑模控制算法与Lyapunov方法相结合，设计基于迭代滑模的船舶动力定位控制器。该算法具有以下优势：（1）既解决了控制算法参数意义不确定问题又进行了稳定性证明;（2）利用积分方法解决了滑模控制算法的抖动问题，稳态误差减小，系统鲁棒性提高;（3）在控制器的设计中增加滑模积分项使系统的收敛速度提高，超调量减小。

1 船舶数学模型

考虑控制器的设计目标，建立包括横荡、纵荡和艏揺运动的三自由度船舶非线性数学模型[14]。

从图1可以看出，在本文提出的控制律的作用下，船舶能够运动到目标位置，并稳定在该目标位置附近极小的范围内，很好地证明了控制律的有效性。

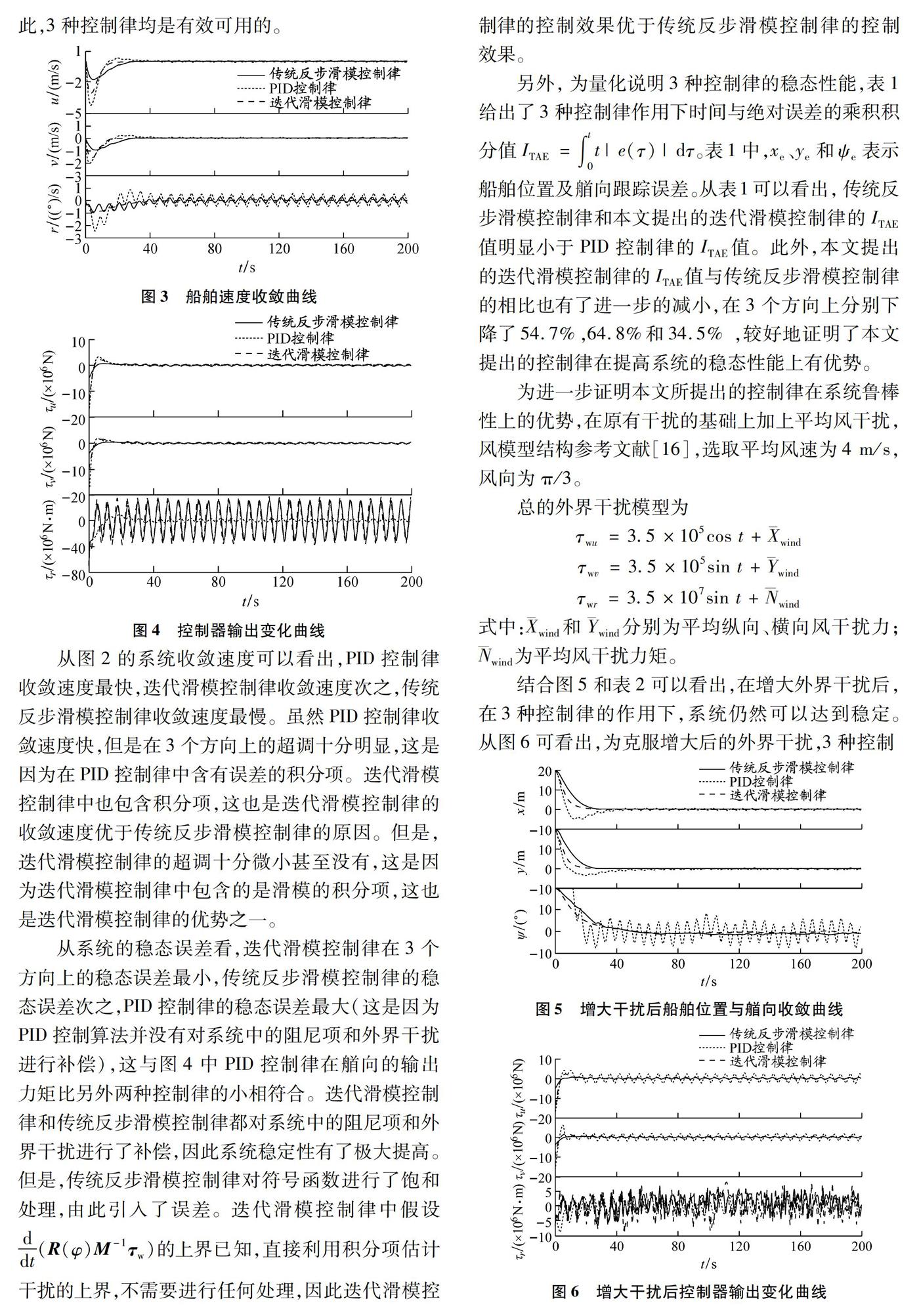
图2表明，在3种控制律（图4）的作用下，系统在x、y、z三个方向上均能够收敛到平衡点附近较小的范围内。从图3可以看出，这3种控制律保证了船舶速度u、v、r均收敛到零附近较小的范围内。因此，3种控制律均是有效可用的。

从图2的系统收敛速度可以看出，PID控制律收敛速度最快，迭代滑模控制律收敛速度次之，传统反步滑模控制律收敛速度最慢。虽然PID控制律收敛速度快，但是在3个方向上的超调十分明显，这是因为在PID控制律中含有误差的积分项。迭代滑模控制律中也包含积分项，这也是迭代滑模控制律的收敛速度优于传统反步滑模控制律的原因。但是，迭代滑模控制律的超调十分微小甚至没有，这是因为迭代滑模控制律中包含的是滑模的积分项，这也是迭代滑模控制律的优势之一。

从系统的稳态误差看，迭代滑模控制律在3个方向上的稳态误差最小，传统反步滑模控制律的稳态误差次之，PID控制律的稳态误差最大（这是因为PID控制算法并没有对系统中的阻尼项和外界干扰进行补偿），这与图4中PID控制律在艏向的输出力矩比另外两种控制律的小相符合。迭代滑模控制律和传统反步滑模控制律都对系统中的阻尼项和外界干扰进行了补偿，因此系统稳定性有了极大提高。但是，传统反步滑模控制律对符号函数进行了饱和处理，由此引入了误差。迭代滑模控制律中

假设ddt（[WTHX]R[WTBX]（φ）

[WTHX]M[WTBX]-1

[WTHX]τ[WTBX]w）的上界已知，直接利用积分项估计干扰的上界，不需要进行任何处理，因此迭代滑模控制律的控制效果优于传统反步滑模控制律的控制效果。

另外，

为量化说明3种控制律的稳态性能，表1给出了3种控制律作用下时间与绝对误差的乘积积分值

ITAE=∫t0t|e（τ）|dτ。

表1中，xe、ye和ψe表示船舶位置及艏向跟蹤误差。

从表1可以看出，

传统反步滑模控制律和本文提出的迭代滑模控制律的ITAE值明显小于PID控制律的ITAE值。此外，本文提出的迭代滑模控制律的ITAE值与传统反步

滑模控制律的相比也有了进一步的减小，在3个方向上分别下降了54.7%，64.8%和34.5% ，较好地证明了本文提出的控制律在提高系统的稳态性能上有优势。

为进一步证明本文所提出的控制律在系统鲁棒性上的优势，在原有干扰的基础上加上平均风干扰，风模型结构

参考文献[16]，选取平均风速为4 m/s，风向为π/3。

总的外界干扰模型为

式中：wind和wind分别为平均纵向、横向风干扰力;wind为平均风干扰力矩。

结合图5和表2可以看出，在增大外界干扰后，在3种控制律的作用下，系统仍然可以达到稳定。

从图6可看出，为克服增大后的外界干扰，3种控制律都开始出现不同程度的抖动，尤其在艏向上的抖动最为严重。

比较表1与表2中的数据发现，

与表1中的ITAE值相比，表2中的ITAE值在3个

方向上都有了不同程度的增加。在PID控制律作用下，xe、ye

和ψe分别增大了43 724.7，29 223和415 910.4，说明PID控制律的鲁棒性最差。此外，

与PID控制律和传统反步滑模控制律相比，本文提出的迭代滑模控制律仍然能够保证ITAE值最小，因此可以证明本文提出的迭代滑模控制律具有更好的鲁棒性。

4 结 论

本文将迭代滑模方法与Lyapunov理论相结合，设计了一种简捷的迭代滑模控制算法并进行了稳定性证明。假设外界干扰变化率上界已知，采用积分策略对外界干扰进行补偿，消除了滑模控制算法的抖动问题。将提出的迭代滑模控制律与PID控制律和传统反步滑模控制律进行了详细的对比分析。结果表明，迭代滑模控制算法具有超调小，收敛速度快，稳定性和鲁棒性好的优点。

参考文献：

[1]FOSSEN T I. Marine control systems： guidance， navigation， and control of ships， rigs， and underwater vehicles[M]. Trondheim： Marine Cybernetics， 2002.

[2]XU Lin， LIU Zhiqing. Design of fuzzy PID controller for ship dynamic positioning[C]//Chinese Control & Decision Conference. IEEE， 2016. DOI： 10.1109/CCDC.2016.7531521.

[3]周春光. BP神经网络PID控制在船舶动力定位系统中的应用[D]. 大连： 大连海事大学， 2016.

[4]ZHANG Guoqing， CAI Yunze， ZHANG Weidong. Robust neural control for dynamic positioning ships with the optimum-seeking guidance[J]. IEEE Transactions on Systems Man & Cybernetics Systems， 2017， 47（7）： 1500-1509. DOI： 10.1109/TSMC.2016.2628859.