上海市科技服务业与制造业互动发展实证研究

郑苏江，吴 忠

（1.上海工程技术大学管理学院，上海 201620；2.上海理工大学管理学院，上海 200093）

近年来，在中国经济发展进入新常态的背景下，制造业与传统服务业、新兴科技产业的互动关联发展势头愈发迅猛。科技服务业作为一种当代新型高端生产性服务业态已然把经济要素与科技要素相连接，不仅增加了制造业生产性服务部门与研发部门的粘性，而且在制造业产业服务化、产业链升级、产品升级、服务升级等方面发挥“助推器”的作用。在国家层面，2016年4月国务院正式发布《上海系统推进全面创新改革试验加快建设具有全球影响力的科技创新中心方案》，明确指出了发展科技服务业的重要意义，并确定了相应的发展目标：计划在2020年前建设成具有全球影响力的科创中心基本框架体系，到2030年着力形成具有全球化影响力的科创中心核心功能，这一目标进一步突显出科技服务业在与装备制造领域及智能制造领域的高质量协同发展需求已经迫在眉睫，相关政策的制定与实施对促进全国科技服务业与制造业的高质量发展也至关重要；在市级层面，根据上海市商务委员会近期公布的统计数据显示：德国化工巨头巴斯夫公司在上海投建了其在亚洲的第3家共创中心，2019年1—8月期间上海市科技服务业已经得到外资10.38亿美元，同比增长幅度高达186.4%，相关指标均创历史新高，科技企业的创新能力与产业孵化能力不断增强。从产业结构横向发展角度出发，以密集型高、附加值大、辐射范围广为特点的科技服务业主要通过渗透效应向相关传统制造业提供知识创新思路，以期大幅度提高生产效率并从高质量层面实现制造业服务化；从产业结构纵向角度出发，科技服务业通过关联效应从制造业全球价值链（GVC）的产品设计、研发、生产、营销、售后等环节进行增值活动，以实现资源的合理配置以及多产业的互动融合发展。因此，面对新一轮的全球化产业变革与科技革命，重点深化研究上海市科技服务业与制造业的高质量互动融合发展有利于制造业新技术、新模式、新业态的形成，并促进新时代背景下制造业的科技资源整合与创新要素集聚。

1 文献回顾

纵观全球科技服务业的发展历程，科技服务机构以资讯类机构的身份最早诞生于19世纪中期，在20世纪中期第三次科技革命的背景下出现了大量新兴科技服务机构，并在20世纪末期初步形成科技服务业态。近年来，基于数字经济的快速发展背景下，云计算、大数据、人工智能等行业的快速兴起，科技服务业已然成为国家重点发展行业，不断深化推进经济发展水平向中高端层次迈进

目前，学术界对于科技服务业与制造业的融合互联发展研究在已有雏形的基础上展开了更深层次的研究：国内学者田振中［1］、司增绰等［2］、周慧妮等［3］、唐晓华等［4］分别以河南省、江苏省、北京市、辽宁省为例，选取不同年限区间及相应地区的投入产出表数据建立面板模型，利用灰色关联分析法与专利系数法并结合本省市的相关政策背景，从制造业技术融合度、产业关联程度、制造业产业升级方向等三个层面对地区科技服务业与制造业协同发展的现状进行了深入研究。梁永福等［5］以台湾时间序列数据为基础建立VAR模型并进行单位根检验与协整检验分析，通过对比广东省研发服务业与制造业的发展现状提出了相应的对策建议；张琴等［6］选取上海、北京、江苏、广东作为样本地区，从竞争效应、知识外溢效应以及产业协同效应等三个层面实证分析了地区科技服务业集聚对制造业发展的影响机制；张鹏等［7］、张媛媛［8］则从制造业与科技服务业的互动发展需求出发，从产业规模、科创能力、服务能力、发展潜力等4个维度构建全国科技服务业发展水平评价指标体系，并对科技服务业与不同技术层次制造业之间的前后向产业关联度进行了动态与静态的研究分析，研究结果显示：全国科技服务业整体发展水平呈现逐年稳步上升的趋势，国内中部、东部、西部的科技服务业发展水平存在明显的板块差异，有关部门需要重点关注制造业与科技服务业的前后向产业关联，进一步提升科技服务业对高端技术制造业的支撑与引领作用。

国外学者一般会把科技服务业称为KIBS知识密集型服务业（Knowledge Intensive Business Services）。Hertog［9］指出科技服务业充当着创新的共同生产者，是科技创新的载体和促进者，他还提出了一个服务创新的四维模型用于进一步分析知识密集型服务在创新中的作用机制。Asikainen［10］认为知识密集型企业是科学技术与市场的知识传递者，在新兴产业研究与创新体系的发展中凸显核心作用。Pina等［11］选取英国362家KIBS企业作为研究对象，通过样板数据深入分析了3个热门行业在研发、设计与创新层面的功能作用。Desmarchelier等［12］构建了一个涉及工业、消费服务业、消费者、KIBS企业和银行系统等主体的多元代理分析模型，重新评估了知识密集型企业与经济增长之间的关系，研究结果显示：科技服务业的发展是经济增长的强大动力，并且可以替代经济增长过程中的物质资本积累，但物质资本积累仍然是经济增长的重要因素。

根据学术界目前的研究现状来看，已有文献更多的是分析科技服务业对制造业的效率、产业关联、协同创新等方面的影响，而从科技服务业与制造业发展互动关系角度展开研究的高质量文献非常少，且研究方法较为单一。因此，本文构建了VAR向量自回归模型与ECM误差修正模型，结合协整检验、Granger因果检验、脉冲响应与方差分解分析方法，通过分析样本指标数据间的长期与短期动态作用机制，实证研究了上海市科技服务业与制造业的产业发展互动关系。

2 数据来源与变量选取

2.1 研究数据

本文研究的时间跨度为2003—2017年，样本数据采用年度数据，数据来源为2004—2018年《中国统计年鉴》《上海统计年鉴》《上海科技统计年鉴》的原始数据经过汇总整理得到。同时，为了保证样本数据的平稳性并消除变量异方差的影响，需要对样本变量进行对数化预处理，其结果分别记为LNRD和LNMAF。图1可以更为直观的展示此时两个变量序列的变化趋势：LNRD和LNMAF的时间序列曲线具有较大的相似性。

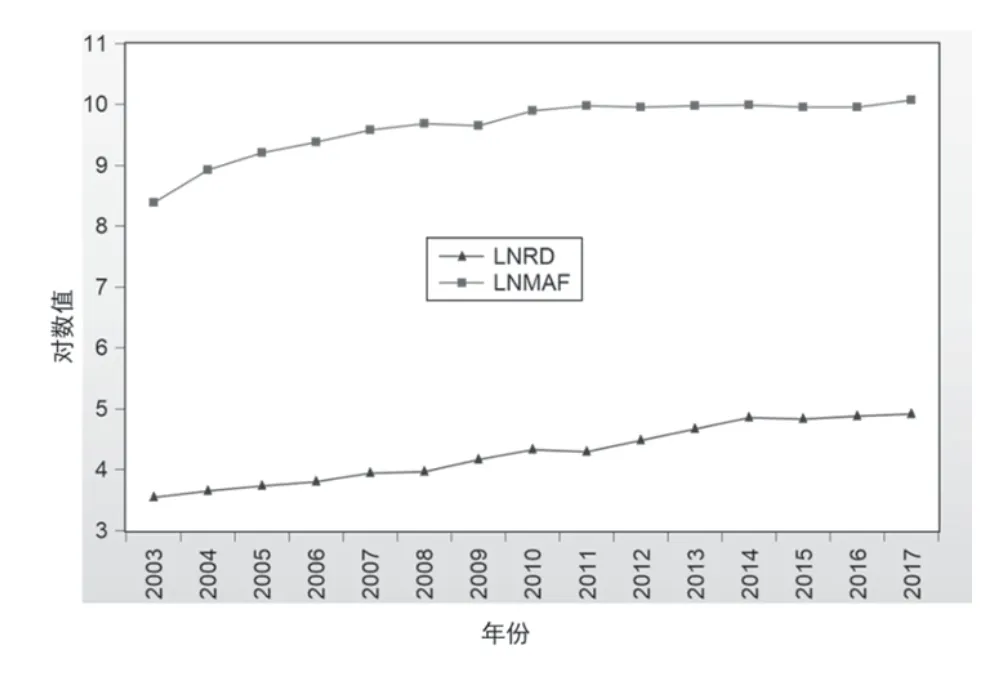
图1 LNMAF&LNRD的时间序列曲线

2.2 变量选取

罗建强等［13］利用灰色关联模型实证研究了南京市科技服务业与制造业之间的互动关联关系，研究结果表明从事科技服务业行业的R&D人员在数量及质量层面对制造业的发展水平影响较大，且R&D经费的使用合理性是影响制造业发展的核心因素。另外考虑到相关数据的可获得性，本文以上海市高技术产业（电子通信设备制造业、电子计算机及办公设备制造业、医疗设备及仪器仪表制造业、航空航天器制造业、医药制造业、信息化学品制造业）的R&D经费支出（RD）作为衡量上海市科技服务业发展程度指标；考虑到相关数据的可获得性，以上海市6个重点发展工业行业（电子信息产品制造业、汽车制造业、石油化工及精细化工制造业、精品钢材制造业、成套设备制造业、生物医药制造业，占全市工业总产值比重约为63.4%～68.9%）的年产值（MAF）作为衡量上海市制造业发展水平指标。

3 实证分析

本文构建了VAR向量自回归模型与ECM误差修正模型，结合脉冲响应与方差分解分析方法，通过采集上海市科技服务业（RD）与制造业（MAF）发展程度的衡量指标数据，并分析该数据间的长期与短期动态作用机制，实证研究了上海市科技服务业与制造业的产业发展互动关系。

3.1 变量平稳性检验

对数据进行平稳性检验是建立时间序列模型的一个前提，导致模型“伪回归”现象出现的一大重要原因就是变量序列不平稳。本文选取ADF(Augmented Dickey-Fuller)单位根检验法对样本数据的平稳性进行检验，滞后阶数M根据SIC准则来确定，检验结果如表1所示。

表1 变量ADF检验结果

结果显示，经过对数化处理后的数据LNRD与LNMAF都不是平稳的时间序列数据，但是经过一阶差分后，ΔLNRD与ΔLNMAF在5%显著性水平下都拒绝原假设（平稳数据）。因此，两组数据均为一阶单整序列，有LNRD～I(1)，LNMAF～I(1)。

3.2 VAR模型的建立

建立VAR模型的核心在于最优滞后期数的选定，其基本思路为：首先任意选定一个滞后阶数，直接建立VAR模型并进行回归分析，然后参考AIC、SC、HQ等五项指标的信息准则来确定最优的滞后期数（如表2所示）。

表2 VAR模型滞后阶数准则信息表

根据表2中的相关准则信息，选取*数量最多的那行指标数据所对应的滞后阶数2作为该VAR模型的最优滞后阶数。因此，以科技服务业发展指标LNRD与制造业发展指标LNMAF两组数据建立VAR（2）模型，对应的VAR模型表达式为：

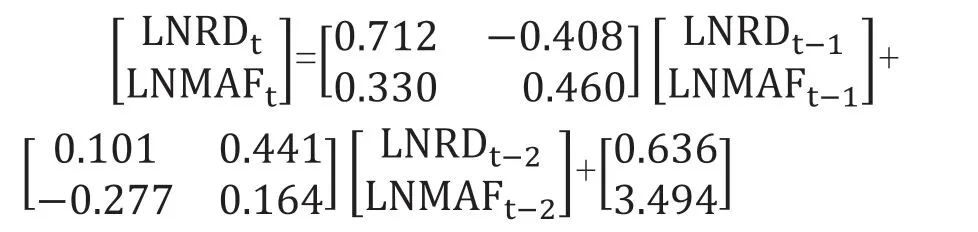
首先，该VAR（2）模型中的各检验统计量均符合检验标准，两个方程的拟合优度值分别为0.978 4、0.950 4，表现出了较好的变量解释能力，且模型方程的整体拟合效果表现良好。其次，在确定最优滞后期数之后，需要对已经建立的VAR（2）进行模型稳定性检验。在一个VAR模型中，AR根的总数计为NM，N表示变量的数目，M表示模型的最优滞后期数，由此可得该VAR（2）模型的AR根数目为2（2个变量）×2（最优滞后期数）=4。本文通过AR根在单位圆的分布情况（图2）来判定模型的稳定性：AR根分布在单位圆内部表明该VAR模型是稳定的，AR根分布在单位圆外部则表明该VAR模型是不稳定的。根据图2可以得到最终模型稳定性检验的结果：该VAR（2）模型的4个根全部位于单位圆内部，模型稳定，满足后续对该模型进行脉冲响应分析与方差分解分析的前提。

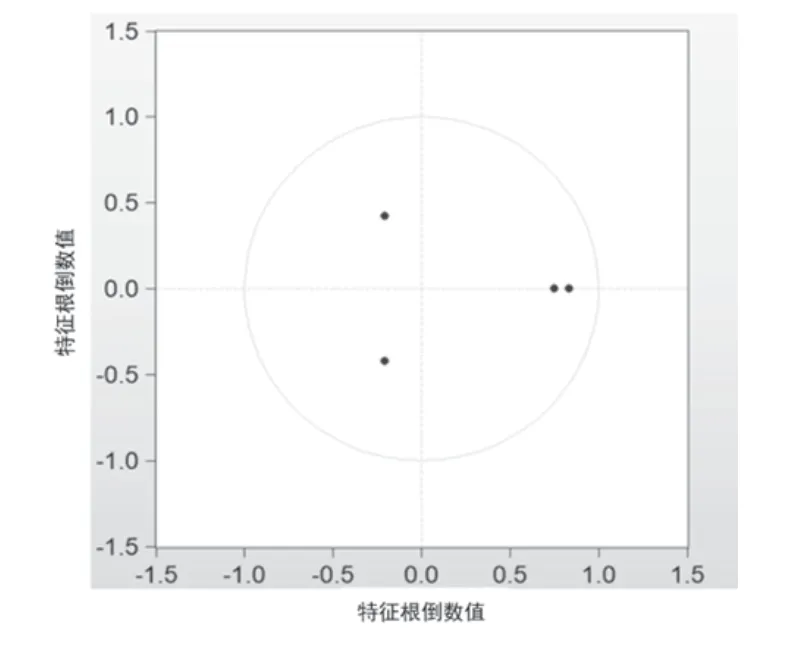
图2 VAR模型稳定性检验结果

3.3 协整检验分析

经过ADF单位根检验可以得出LNMAF与LNRD均为一阶单整序列，为了避免“伪回归”现象的发生，需要进一步对其进行协整检验分析。通过协整检验可以判断多个非平稳变量之间是否存在长期的均衡关系，学术界的主流方法为EG检验与JJ检验。EG检验主要是针对2个变量，通过对两个变量进行OLS回归并检验回归方程残差序列的平稳性；JJ检验则是根据迹检验统计量与最大特征根检验统计量的指标值，结合P值来分析多个变量之间的均衡关系。鉴于LNMAF与LNRD都是一阶单整序列，本文选取EG两步检验方法：

第一步，以LNMAF为被解释变量，LNRD为解释变量，进行OLS回归分析得出协整方程表达式：LNMAF=0.847LNRD+6.024+μt

第二步，对协整回归方程的残差序列进行ADF单位根检验来判定其序列的平稳性，根据SIC准则确定最优滞后期为0，检验结果如表3所示。

表3 协整方程残差μt的ADF检验结果

结果表明回归残差序列μt在1%显著性水平下拒绝原假设，接受不存在单位根的结论（μt为平稳序列）。因此，变量LNMAF与LNRD二者之间存在长期稳定的均衡关系，即：序列LNMAF与LNRD是（1，1）阶协整的。

3.4 ECM误差修正模型

在分析模型的误差修正方面，学术界通常建立ECM模型或VEC模型，ECM模型适用于两个变量的误差修正分析，多个变量的分析一般采用VEC模型。根据上文的变量协整检验分析可知变量LNMAF制造业发展程度指标与LNRD科技服务业发展程度指标之间存在长期均衡关系，且残差序列μt为平稳序列。因此，本文将μt作为误差修正项，建立误差修正模型，根据表4中的模型估计结果可知：信息准则AIC值、SC值、HQ值分别-1.009 672、-0.918 378、-1.018 123，表明样本模型表现情况良好，根据表中参数可得出ECM误差修正模型表达式为：

D(LNMAF)=0.927D(LNRD-0.472(LNMAFt-1-6.024-0.847LNRDt-1)

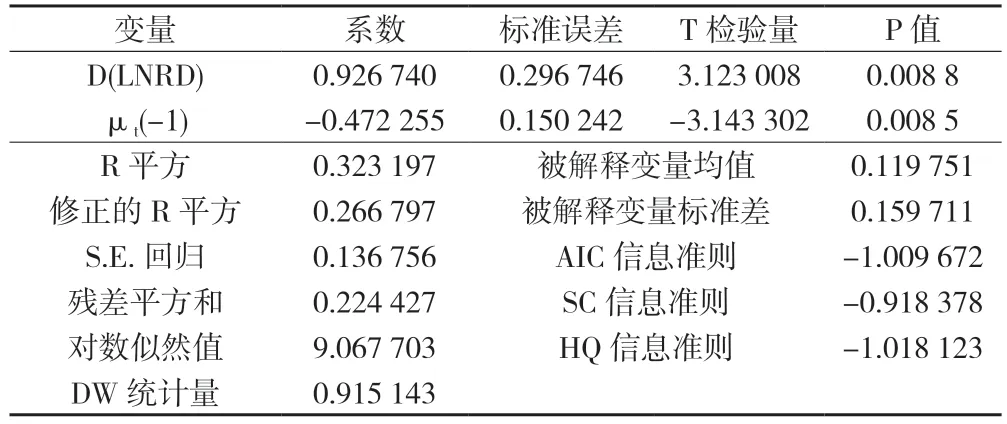
表4 ECM模型估计结果

根据误差修正模型表达式可知，-0.472(LNMAFt-1-6.024-0.847LNRDt-1)为误差修正项，系数-0.472表示误差修正项在模型偏离长期均衡状态时对D(LNMAF)具有负向修正机制：变量在短期内的波动偏离长期均衡状态时，将以47.2%的调整力度从非均衡状态拉回均衡状态。一阶差分项LNMAFt-1-6.024-0.847LNRDt-1表示变量LNMAF与LNRD之间的长期均衡关系。另外，该ECM模型可以反映出被解释变量D(LNMAF)短期波动的影响因素来源于两个部分：一部分源自于解释变量D(LNRD)科技服务业发展程度的短期波动影响，另一部分是反映LNMAF上海市制造业发展程度与LNRD科技服务业发展程度之间长期均衡关系的均衡误差（上一期的LNMAF对均衡水平的偏离程度）。

3.5 Granger因果检验

建立VAR模型的一个重要应用在于分析经济时间序列变量间的因果关系［14］，为了进一步探究两个变量间的长短期均衡关系是否还存在因果关系（检验统计意义上的因果关系），本文采用Granger因果关系检验法(Granger Test of Causality)分析LNRD科技服务业发展的变化与LNMAF制造业发展的变化之间是否存在引起与被引起的关系。由于格兰杰因果关系检验对滞后期数的选择比较敏感，因此本文根据信息准则AIC值最小原则确定最优滞后期数为2，检验结果如表5所示。

表5 LNMAF&LNRD的Granger因果关系检验结果

根据检验结果可知：LNRD科技服务业发展指标与LNMAF制造业发展指标之间仅存在单向因果关系；在5%显著性水平下，当滞后期数为2时，P值分别为0.030 7和0.491 1，拒绝原假设1（LNRD不是LNMAF的格兰杰因），接受原假设2（LNMAF不是LNRD的格兰杰因）；上海市科技服务业的发展是影响制造业发展的格兰杰因，但上海市制造业的发展不是影响科技服务业发展的格兰杰因。因此，上海市科技服务业的发展对相关制造业的发展具有一定的正向推动作用，但制造业的发展并没有明显的刺激科技服务业的发展，且上海市科技服务业与制造业之间的关联互动发展趋势尚未成熟。

3.6 脉冲响应分析

为了进一步研究上海市科技服务业与制造业发展的局部动态关系，本文利用脉冲响应函数（IRF）来说明模型内生变量对于误差出现所产生的反应［15］，以捕捉某个干扰项的冲击因素对所有内生变量在一定时间段内（当前到未来）的影响效应。LNRD科技服务业发展指标与LNMAF制造业发展指标的脉冲响应分析结果如图3所示，图中横坐标代表滞后期数（波动持续的时间长度），纵坐标代表脉冲响应数值（单位冲击引起的波动大小），每个坐标轴内实线部分表示脉冲响应函数，实线两侧的虚线部分表示偏离正负两倍标准差的响应函数。

图3 LNMAF&LNRD的脉冲响应结果

具体表现为：当科技服务业发展指标LNRD在受到自身一个单位正向标准差冲击后，会立即产生强烈的正向响应，并在第一期达到峰值0.092，随后的正向响应幅度逐渐减弱，脉冲响应值在第八期后维持在0.39附近；对LNMAF制造业发展指标施加一个单位正向标准差的冲击之后，LNRD科技服务业发展指标并没有在第一期的时间节点立刻做出响应，而是逐渐产生一定幅度的正向响应趋势并在第四期达到峰值0.039，随后有轻微的负向响应趋势，数值轻微下滑至0.34并在第八期后保持平稳；

对LNRD科技服务业发展指标施加一个单位正向标准差冲击后，制造业发展指标LNMAF立刻做出强烈的响应，后期的响应程度逐渐减弱且存在小幅度波动，脉冲响应数值在第七期后维持在0.06，表明上海市制造业的发展对来自科技服务业的扰动做出了积极地响应，且该正向响应趋势长期稳定存在；当制造业发展指标LNMAF受到了来自自身的单位正向标准差冲击后同样会在第一期迅速给予响应，中期存在一定幅度的正向响应弱化趋势，最终在第六期后基本趋于稳定。

3.7 方差分解分析

方差分解可以进一步分析结构冲击对内生变量变化的影响效应，并对不同结构冲击的贡献度做出评价［16］，本文采用Cholesky分解法对LNRD上海市科技服务业发展指标与LNMAF制造业发展指标的预测均方误差展开分解，结果如表6所示。

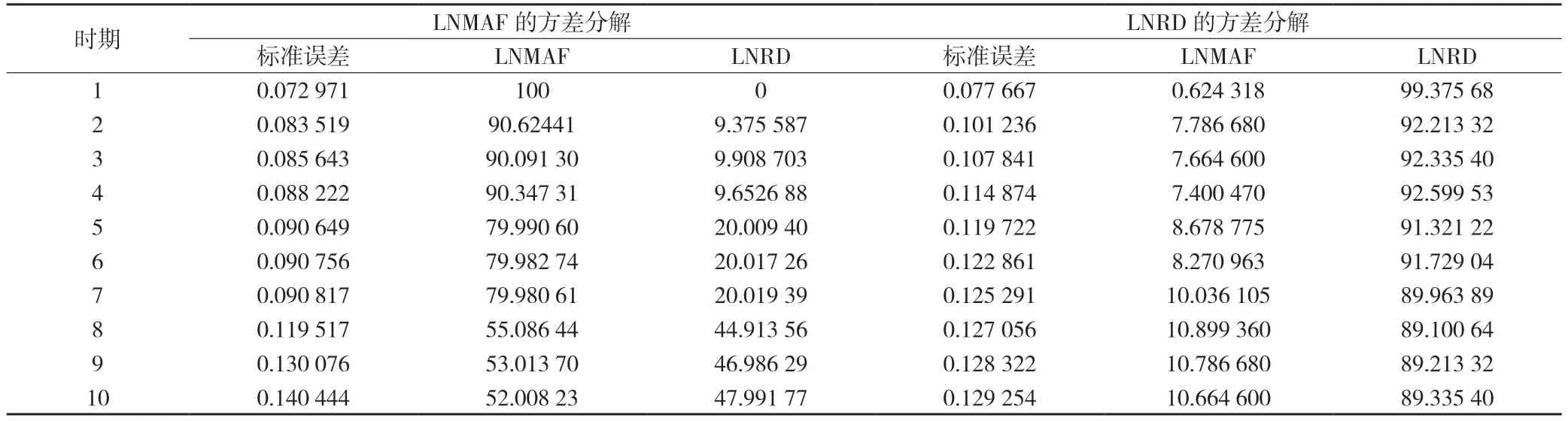
表6 LNMAF&LNRD方差分解结果

在反映制造业发展指标LNMAF的10期方差波动中，有0～47.99%的波动可以由LNRD科技服务业发展指标来解释，其解释能力呈现出缓速增强的趋势并在第八期之后稳定在46%附近；制造业发展指标LNMAF对自身波动的贡献度为52.01%～100%，其自身贡献度的变化呈现阶梯型弱化趋势，最终在第八期后基本稳定，总体可以反映出上海市科技服务业的发展指标对制造业的发展指标存在较为显著的长期波动影响。

在反映科技服务业发展指标LNRD的10期方差波动中，有0.62%～11.66%的波动可以由LNMAF制造业发展指标来解释，其影响程度从第二期开始趋于平稳，波动水平维持在7%～10%之间；科技服务业发展指标LNRD对自身的贡献度第一期为99.38%，在第二期的下降幅度最大，后期保持在89%的贡献度水平，这也反映出上海市科技服务业的发展在很大程度上是依靠自身，制造业的发展并没有对科技服务业的发展产生较大的推动力，二者之间的互动融合发展成效有待进一步优化与完善。

4 研究结论

（1）协整检验分析结果：变量LNMAF制造业发展指标与LNRD科技服务业发展指标二者之间存在长期稳定的均衡关系，即：序列LNMAF与LNRD是（1，1）阶协整的。

（2）ECM误差修正模型分析结果：长期均衡对于LNMAF和LNRD的短期波动影响在统计上是显著的，被解释变量D（LNMAF）短期波动的影响因素来源于两个部分：一部分源自于解释变量D（LNRD）科技服务业发展程度的短期波动影响，另一部分是反映LNMAF上海市制造业发展程度与LNRD科技服务业发展程度之间长期均衡关系的均衡误差（上一期的LNMAF对均衡水平的偏离程度）。

（3）Granger因果关系检验结果：LNRD科技服务业发展指标与LNMAF制造业发展指标之间仅存在单向因果关系，上海市科技服务业的发展是影响制造业发展的格兰杰因，但上海市制造业的发展不是影响科技服务业发展的格兰杰因。表明上海市科技服务业的发展对相关制造业的发展具有一定的正向推动作用，但制造业的发展并没有显著的刺激科技服务业的发展，使得上海市科技服务业与制造业之间的关联互动发展趋势尚未成熟。

（4）脉冲响应分析结果：LNRD科技服务业发展指标与LNMAF制造业发展指标这个两个变量不仅会受到显著的自身冲击影响，而且二者在短期内存在相互的正向响应效应（LNRD对LNMAF的响应程度更为显著），该响应长期存在并在一定时期后趋于平稳，表明上海市制造业的发展对来自科技服务业的扰动做出了积极地响应，且该正向响应趋势长期稳定存在。

（5）方差分解分析结果：在LNRD与LNMAF的10期方差波动中，LNRD科技服务业发展指标对LNMAF制造业发展指标存在一定的长期波动影响，相比之下，LNRD对LNMAF的波动影响要大于LNMAF对LNRD的波动影响。总体可以反映出上海市科技服务业的发展对制造业的发展产生了较为显著的长期波动影响，二者之间的互动融合发展成效有待进一步优化与完善。