直觉模糊软半环的软像与软逆像

李 庆，熊 涛

(1.重庆师范大学 数学科学学院，重庆 400047；2.西华师范大学 数学与信息学院，四川 南充 637002)

0 引言

1986年,保加利亚学者K. T. Atanassov[1]在模糊集的基础上提出了直觉模糊集的概念。直觉模糊集比传统的模糊集在处理模糊性和不确定性等方面更具有灵活性和实用性。软集理论(Softsettheory)是D. Molodtsov[2]提出用来处理不确定性问题的新的数学工具。软集理论的引入有效地解决了参数化工具不足的问题。为了充分发挥软集理论和直觉模糊集理论的优点,学者们提出了直觉模糊软集理论[3-4]。随之有研究者尝试把直觉模糊软集理论和不同的代数结构结合起来研究[5-8]。参考文献[9-10]引入了直觉模糊软半环和直觉模糊软半环的直觉模糊软理想的概念，丰富和拓宽了直觉模糊软集理论及半环理论。半环概念最早是由P.Dedekind于1894年在代数数论的原著中提出的。二十世纪六十年代开始，随着信息科学、理论计算机科学的发展，半环代数理论及其应用都得到迅速发展。半环是对环和完备格非常自然的推广。在数学的分支密码学、泛函分析、拓扑学和欧氏几何等里面，都有着半环理论的思想。半环还在物理学、化学、建筑、信息与通讯、理论计算机科学等自然科学与技术领域里都有广泛和深入的应用。现在，有不少关于半环理论和应用的专著出现，相关理论已十分丰富[11-15]。代数结构之间的联系往往可以通过一些映射反映出来。同态既能反映两个代数结构元素之间的联系，也能反映彼此结构上的联系，比如运算的保持，等等。对于同构的两个代数系统更是可以视作是一样的，只是表现形式不一样。正因为如此，研究一个代数结构的同态像和逆像就很有必要。我们可以通过其同态像和逆像来获知该代数对象本身的一些性质，这是研究直觉模糊软半环在直觉模糊软映射下的软像与软逆像的意义所在。

在此基础之上，我们自然想到映射如何作用于直觉模糊软半环，直觉模糊软半环在映射下的像与逆像是否还是直觉模糊软半环？本文对此作了研究。同时，还证明了直觉模糊软(左，右)理想在直觉模糊软映射下的软像与软逆像仍是直觉模糊软(左，右)理想。

本文使用的概念和符号都是标准的。例如：IFS是论域上的直觉模糊集等，在以后使用时不再特别说明。

1 预备知识

定义1.1[1]：论域X上的直觉模糊集(IFS)是指：A={〈x,μA(x),λA(x)〉|x∈X}。其中μA(x):X→[0,1],λA(x):X→[0,1],满足0≤μA(x)+λA(x)≤1(∀x∈X)。μA(x)和λA(x)分别为X中元素x属于A的隶属度和非隶属度。πA(x)=1-μA(x)-λA(x)称为X中元素x属于A的犹豫度。

定义1.2[3]：设U表示初始论域,E表示与U中对象有关的所有参数之集，P(U)表示U上的所有直觉模糊集的集合。令A⊆E,二元组(F,A)称为U上的直觉模糊软集，其中F:A→P(U)是一个映射。

定义1.3[10]：设R是一个半环,R上的一个直觉模糊集∅≠A={〈x,μA(x),λA(x)〉|x∈R}称为R的直觉模糊半环,若满足对所有r1,r2∈R，则：

(a)μA(r1+r2)≥μA(r1)∧μA(r2),λA(r1+r2)≤λA(r1)∨λA(r2)；

(b)μA(r1r2)≥μA(r1)∧μA(r2),λA(r1r2)≤λA(r1)∨λA(r2)。

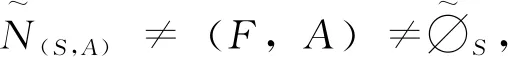
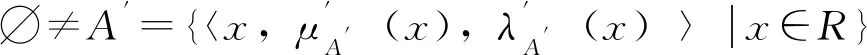
(a)A′⊆A；

定义1.6[10]：设初始论域为半环S,E表示与S中对象有关的所有参数之集。令A,B⊆E，(F,A)和(G,B)是半环S上的两个直觉模糊软半环，直觉模糊软半环(G,B)称为(F,A)的直觉模糊软子半环，若满足：

(a)B⊆A；

(b)当G(b)≠∅时，G(b)是F(a)的直觉模糊子半环。

2 直觉模糊软半环的软像和软逆像

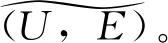
F(a)=M={〈u1,μM(u1),λM(u1)〉|u1∈U1},G(b)=N={〈u2,μN(u2),λN(u2)〉|u2∈U2};

μN(u2)=

λN(u2)=

(F,A)在直觉模糊软映射f=(f1,f2)下的像记为f(F,A)。

定理2.4 设(F,A)是半环S上的一个直觉模糊软集，(F,A)是半环S上的一个直觉模糊软半环当且仅当对所有r,t∈[0,1]和a∈A,F(a)(r,t)是S的子半环。

证明：假设(F,A)是半环S上的直觉模糊软半环。对所有r,t∈[0,1],a∈A和s1,s2∈F(a)(r,t)，我们有μF(a)(s1)≥r,λF(a)(s1)≤t,μF(a)(s2)≥r,λF(a)(s2)≤t。由定义，F(a)是S的直觉模糊半环。因此

μF(a)(s1+s2)≥μF(a)(s1)∧μF(a)(s2)≥r，

λF(a)(s1+s2)≤λF(a)(s1)∨λF(a)(s2)≤t，

μF(a)(s1s2)≥μF(a)(s1)∧μF(a)(s2)≥r，

λF(a)(s1s2)≤λF(a)(s1)∨λF(a)(s2)≤t。

亦即s1+s2,s1s2∈F(a)(r,t),所以,对所有r,t∈[0,1]和a∈A,F(a)(r,t)是S的子半环。

反之，假设对所有r,t∈[0,1]和a∈A,F(a)(r,t)是S的子半环。对每一个a∈A和s1,s2∈S，令r=μF(a)(s1)∧μF(a)(s2),t=λF(a)(s1)∨λF(a)(s2)，则s1,s2∈F(a)(r,t)。

因为F(a)(r,t)是S的子半环,有s1+s2,s1s2∈F(a)(r,t)。亦即

μF(a)(s1+s2)≥r=μF(a)(s1)∧μF(a)(s2)，

λF(a)(s1+s2)≤t=λF(a)(s1)∨λF(a)(s2)，

μF(a)(s1s2)≥r=μF(a)(s1)∧μF(a)(s2)，

λF(a)(s1s2)≤t=λF(a)(s1)∨λF(a)(s2)。

因此，对所有a∈A,F(a)是半环S的直觉模糊半环。故(F,A)是半环S上的直觉模糊软半环。

注：此定理给出了证明半环S上的一个直觉模糊软集(F,A)是半环S上的一个直觉模糊软半环的方法。

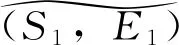
证明：令(G,B)在直觉模糊软映射f=(f1,f2)下的逆像是f-1(G,B)=(F,A)(f2-1(B)=A⊆E1,B⊆E2)。令a∈f2-1(B)=A,f2(a)∈B，对每一个f2(a)∈B,G(f2(a))是S2的直觉模糊半环。对所有s′,s″∈S1,

μF(a)(s′s″)=μG(f2(a))f1(s′s″)=μG(f2(a))(f1(s′)f1(s″))≥μG(f2(a))f1(s′)∧μG(f2(a))f1(s″)=μF(a)(s′)∧μF(a)(s″),

λF(a)(s′s″)=λG(f2(a))f1(s′s″)=λG(f2(a))(f1(s′)f1(s″))≤λG(f2(a))f1(s′)∨λG(f2(a))f1(s″)=λF(a)(s′)∨λF(a)(s″),

μF(a)(s′+s″)=μG(f2(a))f1(s′+s″)=μG(f2(a))(f1(s′)+f1(s″))≥μG(f2(a))f1(s′)∧μG(f2(a))f1(s″)=μF(a)(s′)∧μF(a)(s″),

λF(a)(s′+s″)=λG(f2(a))f1(s′+s″)=λG(f2(a))(f1(s′)+f1(s″))≤λG(f2(a))f1(s′)∨λG(f2(a))f1(s″)=λF(a)(s′)∨λF(a)(s″)。

因此F(a)是S1的一个直觉模糊半环。由a的任意性,f-1(G,B)=(F,A)是S1上的一个直觉模糊软半环。

μG(b)(s1)≥r,λG(b)(s1)≤t,μG(b)(s2)≥r,λG(b)(s2)≤t，

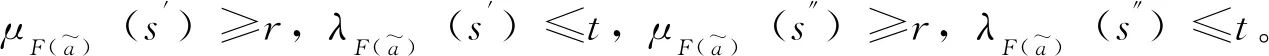
此表明s1+s2,s1s2∈G(b)(r,t)，故对所有b∈B,r,t∈[0,1],G(b)(r,t)是S2的一个子半环。由b的任意性，(F,A)在直觉模糊软映射f=(f1,f2)下的像是S2上的一个直觉模糊软半环。

3 直觉模糊软左(右)理想的软像和软逆像

在这里，我们首先引入直觉模糊软半环的直觉模糊软理想的概念：

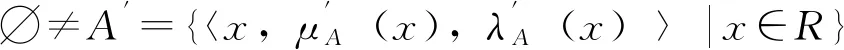
(a)A′是A的一个直觉模糊子半环；

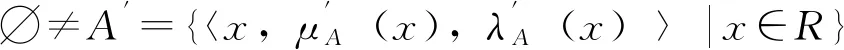
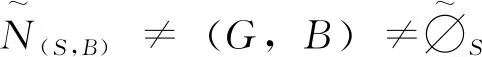
定理3.3 设(F,A)是半环S上的一个直觉模糊软集，则(F,A)是半环S上的一个 直觉模糊软左(右)理想当且仅当对所有r,t∈[0,1]和a∈A，F(a)(r,t)={x∈S|μF(a)(x)≥r,λF(a)(x)≤t}是S的一个左(右)理想。

证明：假设(F,A)是半环S上的一个直觉模糊软左(右)理想。那么，当F(a)≠∅时,F(a)是S的一个直觉模糊左(右)理想。故对所有s1,s2∈S，

μF(a)(s1+s2)≥μF(a)(s1)∧μF(a)(s2)，

λF(a)(s1+s2)≤λF(a)(s1)∨λF(a)(s2)，

μF(a)(s1s2)≥μF(a)(s2)(μF(a)(s1))，

λF(a)(s1s2)≤λF(a)(s2)(λF(a)(s1))。

对所有b1,b2∈F(a)(r,t)，s∈S，我们可得：

μF(a)(b1+b2)≥μF(a)(b1)∧μF(a)(b2)≥r，

λF(a)(b1+b2)≤λF(a)(b1)∨λF(a)(b2)≤t，

μF(a)(sb2)≥μF(a)(b2)≥r(μF(a)(b1s)≥μF(a)(b1)≥r)，

λF(a)(sb2)≤λF(a)(b2)≤t(λF(a)(b1s)≤λF(a)(b1)≤t)。

故对所有r,t∈[0,1]和a∈A,b1+b2,sb2(b1s)∈F(a)(r,t),F(a)(r,t)是S的左(右)理想。

另一方面,F(a)≠∅,对所有r,t∈[0,1]和a∈A,令F(a)(r,t)={x∈S|μF(a)(x)≥r,λF(a)(x)≤t}是S的左(右)理想。对每个a∈A,s′∈S,令r=μF(a)(s′)，t=λF(a)(s′)，则s′∈F(a)(r,t)。因为F(a)(r,t)是S的左(右)理想，所以对每个s∈S，我们有

μF(a)(ss′)≥r=μF(a)(s′)，λF(a)(ss′)≤t=λF(a)(s′)，故ss′∈F(a)(r,t)。

(μF(a)(s′s)≥r=μF(a)(s′)，λF(a)(s′s)≤t=λF(a)(s′)，故s′s∈F(a)(r,t))。

下面我们将证明s+s′∈F(a)(r,t)。对每个s,s′∈S,令r=μF(a)(s)∧μF(a)(s′)，t=λF(a)(s)∨λF(a)(s′)，则s,s′∈F(a)(r,t)，故

μF(a)(s+s′)≥r=μF(a)(s)∧μF(a)(s′)，

λF(a)(s+s′)≤t=λF(a)(s)∨λF(a)(s′),

则当F(a)≠∅时,F(a)是S的一个直觉模糊左(右)理想。因此(F,A)是S上的一个直觉模糊软左(右)理想。

证明：令(G,B)在直觉模糊软映射f=(f1,f2)下的逆像是f-1(G,B)=(F,A)(f2-1(B)=A⊆E1,B⊆E2)，令a∈f2-1(B)=A,f2(a)∈B,对每个f2(a)∈B,G(f2(a))是S2的一个直觉模糊左(右)理想。因此对所有s′,s″∈S1。

μF(a)(s′s″)=μG(f2(a))f1(s′s″)=μG(f2(a))(f1(s′)f1(s″))≥μG(f2(a))f1(s″)=μF(a)(s″)，

(μF(a)(s′s″)=μG(f2(a))f1(s′s″)=μG(f2(a))(f1(s′)f1(s″))≥μG(f2(a))f1(s′)=μF(a)(s′))，

λF(a)(s′s″)=λG(f2(a))f1(s′s″)=λG(f2(a))(f1(s′)f1(s″))≤λG(f2(a))f1(s″)=λF(a)(s″)，

(λF(a)(s′s″)=λG(f2(a))f1(s′s″)=λG(f2(a))(f1(s′)f1(s″))≤μG(f2(a))f1(s′)=λF(a)(s′))，

μF(a)(s′+s″)=μG(f2(a))f1(s′+s″)=μG(f2(a))(f1(s′)+f1(s″))≥μG(f2(a))(f1(s′))∧μG(f2(a))f1(s″)=μF(a)(s′)∧μF(a)(s″)，

λF(a)(s′+s″)=λG(f2(a))f1(s′+s″)=λG(f2(a))(f1(s′)+f1(s″))≤λG(f2(a))(f1(s′))∨λG(f2(a))f1(s″)=λF(a)(s′)∨λF(a)(s″)。

从而推出F(a)是S1的一个直觉模糊左(右)理想，由a的任意性，f-1(G,B)=(F,A)是S1上的一个直觉模糊软左(右)理想。

对所有s1,s2∈G(b)(r,t)，μG(b)(s1)≥r,λG(b)(s1)≤t，μG(b)(s2)≥r,λG(b)(s2)≤t，

从而u2s1∈G(b)(r,t)。下面我们证明对所有s1,s2∈G(b)(r,t)⊆S2,s1+s2∈G(b)(r,t)。

因为f1∶S1→S2是一个同态满射，f1(x′+x″)=s1+s2,因此x′+x″∈f1-1(s1+s2)。

所以我们有u2s1∈G(b)(r,t)，s1+s2∈G(b)(r,t)，这表明对所有b∈B,r,t∈[0,1],G(b)(r,t)是S1的一个直觉模糊左理想。因此(G,B)是S2上的一个直觉模糊软左理想。

4 小结

本文证明了直觉模糊软半环的软像和软逆像仍是直觉模糊软半环。直觉模糊软(左，右)理想在直觉模糊软映射下的软像与软逆像仍是直觉模糊软(左,右)理想。这表明直觉模糊软半环、直觉模糊软理想与它们的像和逆像之间有着相似的代数性质。作为直觉模糊软集理论在半环这个代数结构上的应用，直觉模糊软半环的其他性质还值得我们去研究。