深海半潜平台主尺度优化

童 波 袁清宁 裴志勇 吴卫国

(中国船舶工业集团公司第七〇八研究所1) 上海 200011) (武汉理工大学交通学院2) 武汉 430063)

0 引 言

深水油气开发中浮式生产平台主要有张力腿平台(TLP)、单柱式平台(Spar)和半潜式平台.TLP平台的垂荡响应较小，但是随着水深超过1 500 m时造价会增大很多，同时张力腿的设计和安装也十分复杂.Spar平台不再受水深的限制，然而其上层建筑和浮体必须在海上进行安装，因此安装成本十分高昂，此外由于甲板上的空间限制,Spar平台的装载能力较差.半潜式平台拥有更广泛的适用水深、更强的装载能力，更低的建造和安装成本，同时由于上部模块扩展性强，耐波性能优异，其安全性能也优于前两种平台，因此半潜平台成为当前备受青睐的一种深海装备.由于长期在目标海域作业，遭遇的海况复杂多变，所以此类型平台对水动力性能的要求远远大于其他类型平台.

宋兴宇[1]对一半潜平台计算其水动力特性，分析了平台水动力性能与不同主尺度参数之间的影响关系，明确了平台吃水和立柱间距对垂荡性能的影响，提出了主尺度参数优化工作的指导思想.童波等[2]对深水半潜平台的各组件进行了详细的研究，分析了各组件对平台性能的影响，提出了主尺度参数与设计指标间的关系，论证了影响主尺度选取的各个因素.Akagi等[3]通过建立以圆柱形浮体的截面直径和浮体长度为主尺度变量、以作业海况下平台垂荡响应的均方差最小为优化目标的优化模型，采用序列二次规划算法，对平台进行了优化，结果显示垂荡性能得到了提高.陈新权等[4]采用响应面模型拟合一超深水半潜平台主尺度与垂荡响应之间的关系，基于模型采用多岛遗传算法和序列二次规划算法的组合优化策略对其进行主尺度优化，以达到更好的垂荡响应，结果表明此方法较传统的基于试算和误差评估的小范围寻优方法，能在得到全局最优解的同时大大减少优化分析时间.胡志强[5]采用协同优化算法，不只是对半潜平台的运动性能，还对横摇、气隙、稳性、环境阻尼、水平位移等进行了多目标的设计优化工作，结果显示并非每一次的优化过程都能获得满足所有约束变量要求的优化结果.周佳等[6]引入Pareto解的概念，采用试验设计和近似模型相结合的方法，以垂荡运动最小为优化目标，运用非受控排序多目标遗传算法对深水半潜平台进行了优化分析，最优结果接近Pareto前沿，即该结果方案是最优的主尺度设计方案.白云山[7]在此基础上对平台造价和垂荡同时进行优化，得出了造价和垂荡的Pareto前沿，为深水半潜平台确定合理的主尺度提供了可靠的参考依据.

本文研究中，设定典型的六个主尺度为参数变量并考虑实际情况确定他们的变化范围，根据主尺度与平台性能的关系以垂荡、纵摇和横摇的运动响应为目标函数，考虑规范条文的规定和实际的要求，设定初稳性高和排水量的约束条件，采用试验设计中的最优拉丁超立方法对变量进行抽样取值，选取200种方案组合，运用Sesam软件计算各方案的水动力性能，通过径向基代理模型来近似模拟主尺度变量与垂荡、纵摇和横摇等运动响应的关系，基于近似模型采用NSGA-Ⅱ算法对各两种运动响应组合进行优化分析，得出Pareto解集，所有可行方案中靠近Pareto前沿的为最优方案.

1 优化系统构建

1.1 优化参量

深海半潜平台为适应各种复杂海况及工作状况，其结构设计得非常复杂，主尺度特征参数众多，通过对运动响应进行计算分析确定合理的主尺度参数涉及各种变量.平台吃水、下浮体横向间距、船体惯性矩等决定了垂荡运动的频率及响应；平台吃水、重心高度、船体惯性矩等对深海半潜平台的横摇和纵摇起着重要作用.平台主尺度与设计指标间的关系见图1.

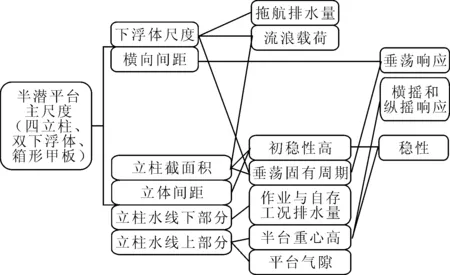
图1 半潜平台主尺度与设计指标参数关系

根据深海半潜平台结构特点，考虑各典型尺度对运动响应的影响，如重心高度主要由立柱水线上部分高度决定，初稳性高受立柱间距及高度的影响最大.在本研究中选取下浮体长度x1、宽度x2及高度x3，立柱横向间距x4、纵向间距x5，立柱高度x6等六个典型主尺度要素作为设计变量，见图2.

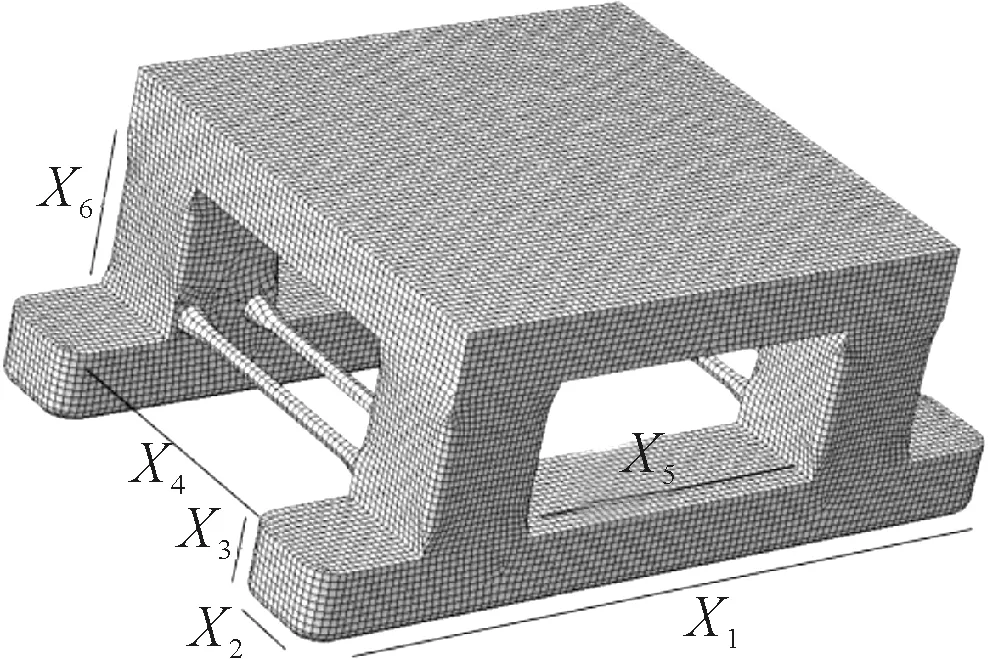
图2 典型设计变量示意图

在本研究中以一标准型深水半潜式生产平台为母型，各变量的变化范围取10%，即各相应尺度变量值的90%～110%，通过试验设计采用最优拉丁超立方法进行抽样，共抽取200组方案，设计变量的变化范围及增量步见表1.

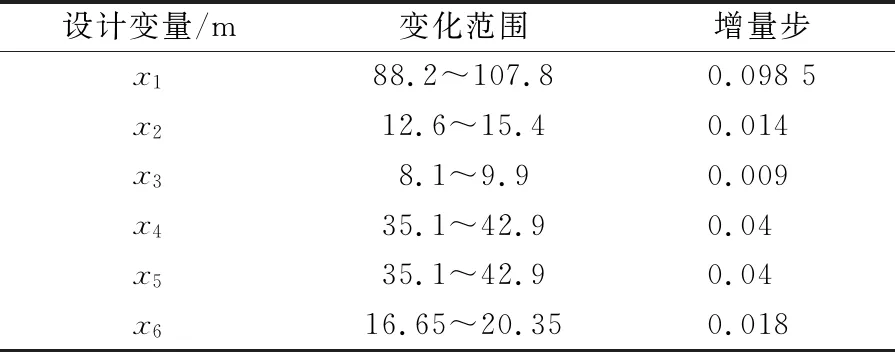
表1 设计变量变化范围及增量步

1.2 目标函数

由于深海半潜式平台需要长期在目标海域作业，可能遭遇的海况复杂多样，又由于其结构特点，在海洋环境中受到风、浪、流的联合作用，平台的横摇、纵摇和垂荡响应对平台的安全作业、拖航、风暴自存等都有着重要的影响，因此深海半潜式平台的主尺度优化主要考虑横摇、纵摇和垂荡的运动响应.

1) 垂荡响应 深海半潜式平台的垂荡性能是该平台能否正常作业的关键指标.半潜式平台的垂荡响应比Spar、TLP等平台大很多.半潜式平台的垂荡响应幅度一般要求小于2 m，垂荡响应过大将会导致平台无法正常作业甚至会对平台的安全性产生影响.因此，对主尺度设计的优化来减小半潜式平台在波浪中的垂荡响应具有重要意义.通过用Seasam软件对平台的水动力性能计算，迎浪下的垂荡响应最显著，所以本文采用单位波迎浪下的垂荡响应值进行分析.

2) 横摇响应和纵摇响应 横摇、纵摇性能将会影响平台能否正常作业，如果横摇、纵摇过大将会导致甲板上很多设备无法正常运转，还会导致人员身体不适.通过水动力计算，在横浪时横摇响应最显著，迎浪时纵摇最显著.因此,分别采用横浪时的横摇响应值，迎浪时的纵摇响应值进行分析.

1.3 约束条件

在优化过程中可能会出现目标函数结果良好，但平台其他性能超出规范和实际使用要求的的情况，因此需要对整个优化过程设定一定的约束条件.为了保证平台的优化结果满足要求，本次研究选取初稳性高和排水量作为约束条件.

1) 平台主尺度优化过程中尺度变化的范围不大，一般可忽略尺度变化对平台重心的影响，考虑到下浮体尺度的变化会造成排水体积的变化，根据实际使用的要求，本文取排水量的变化范围不超过±5%.

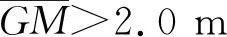
综上所述，建立以垂荡、横摇和纵摇响应最小为目标函数，以排水量不超过母型平台排水量的±5%和初稳性高大于2 m为约束条件，寻找最优的主尺度方案的优化模型如下.

Findx1,x2,x3,x4,x5,x6

minheave，roll，pitch

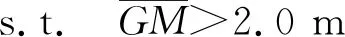
29 598 156≥displacement≥28 437 444

1.4 优化分析系统

进行深海半潜式平台主尺度优化时，先确定主尺度参数，在其变化范围内通过最优拉丁超立方法抽取方案样点，随后确定目标函数，对所有方案计算其运动响应，再运用径向基模型近似模拟目标函数和主尺度参数的关系，在既定的约束条件下进行优化计算，得到Pareto解集，靠近Pareto前沿的解为最优方案.优化分析流程见图3.

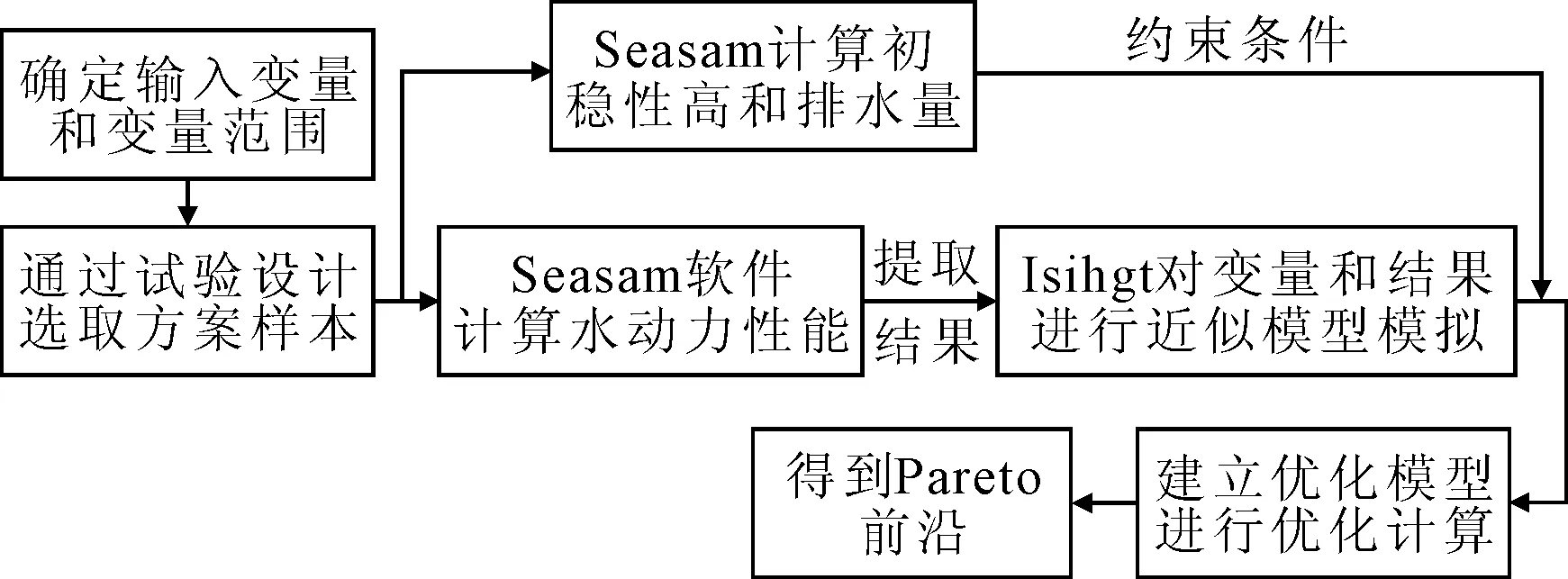
图3 半潜平台优化分析流程图

2 试验设计技术

试验设计是关于如何按照预定目标制订适当的实施方案，以利于对实验结果进行有效的统计分析的数学原理和实施方法，目的是在设计空间中选取具有代表性的样本点.目前常用的试验设计方法有参数试验、正交数组、中心组合设计、拉丁超立方设计和最优拉丁超立方设计等.本文研究采用最优拉丁超立方法来进行试验设计.

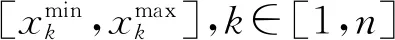
拉丁超立方设计具有高效的空间填充能力，采用分层的思想提升了抽样效率.因为它是用随机组合的方式来生成设计矩阵的，所以不可重复，而且可能存在试验点分布不够均匀的情况.最优拉丁超立方设计[10-11]在拉丁超立方的基础上采用算法使因子和响应的拟合更加精确真实，使所有的试验点尽量均匀分布在整个设计空间从而提高了抽样的均匀性.在同样的设计空间和样本点的条件下，两种方法的对比见图4.

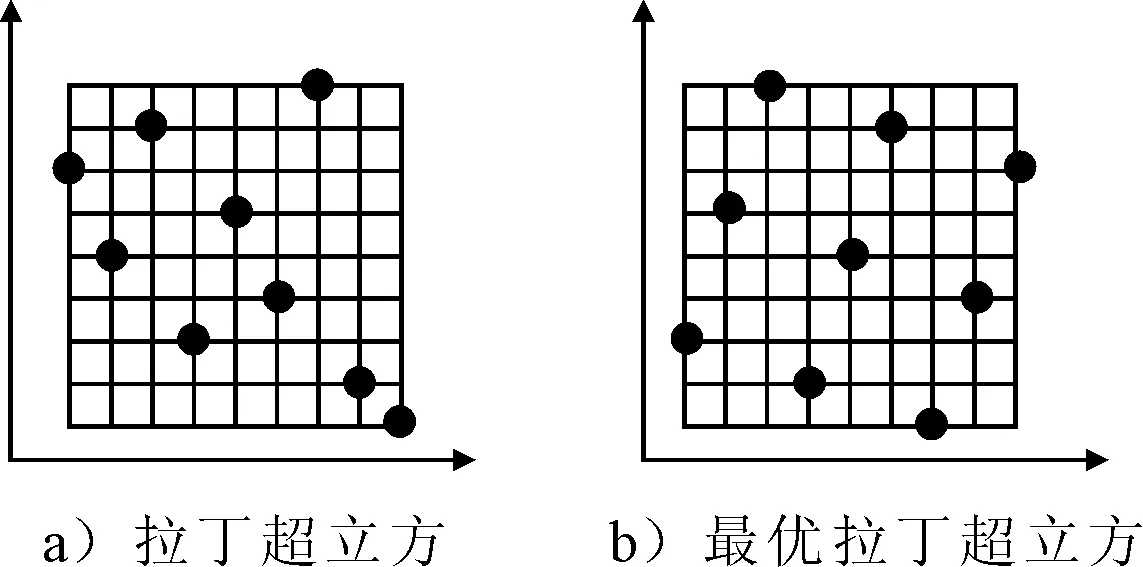
图4 拉丁超立方和最优拉丁超立方对比

3 近似模型和优化算法

3.1 近似模型

常用的近似模型主要有响应面模型(RSM)、径向基模型(RBF)、克里格模型(Kriging).响应面模型可以用少量的点比较精确的拟合函数关系，所以在拟合非线性程度低的函数关系式常采用此方法；而克里格模型可以很好的拟合非线性较高的问题，但当参数为高斯函数的各向异性时优化计算十分缓慢；径向基模型拟合复杂非线性函数的能力非常强，同时有很强的容错性[12-13].由于平台主尺度与水动力性能具有很强的非线性，所以选取径向基模型作为近似模型.径向基RBF网络以待测点和样本点之间的欧几里得距离为自变量，即假设x1,x2,…,xN∈RN代表一组输入变量，gi≡g(‖x-xj‖c)∈R,(j=1,2,…,N)是基函数，其中‖x-xj‖是欧几里得距离(x-xj)T(x-xj)，且0.2≤c≤3.

通过对运动响应与主尺度变量模拟的近似模型可以得到各主尺度要素对运动响应的影响程度，不同主尺度要素的敏感度分析见图5.图5a)为纵摇响应对各变量敏感性结果，可以看出下浮体高度x3的影响最大，下浮体宽度x2、立柱横向间距x4次之，立柱纵向间距x5影响最小；从横摇敏感性分析图中可以看出下浮体高度x3对横摇响应的影响也最大，下浮体宽度x2、立柱高度x6次之，立柱横向间距x4影响最小；从垂荡敏感性分析图中可见下浮体宽度x2的影响最大，下浮体高度x3、下浮体长度x1次之，立柱纵向间距x5影响最小.

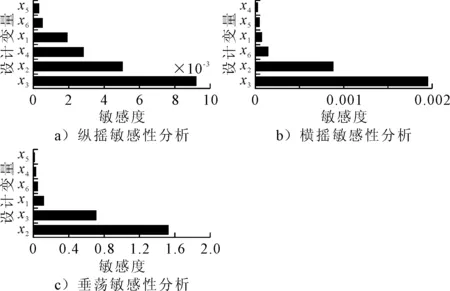
图5 近似模型运动响应敏感性分析图

径向基模型的精度可以通过复相关系数R2来评价.定义为

(1)

表2 径向基模型近似误差

基于近似模型拟合的纵摇、横摇和垂荡的响应面可分别通过两个主尺度要素来描述.纵摇响应随下浮体高度增加而变大，非线性程度不高，关于浮体宽度和浮体高度的响应面近似为斜面，然而与立柱横向间距关系非线性很强，关于浮体高度和立柱横向间距的响应面出现了最低点和最高点.横摇响应与各尺度参数关系非线性程度弱，响应面基本为斜面.垂荡响应与各尺度参数关系非线性程度很强，响应面出现多个峰值和谷值.典型响应面与各主尺度要素关系见图6.

图6 典型响应面与主尺度要素关系图

3.2 优化分析

当目标函数是由两个或两个以上独立的指标组成时就称为多目标优化问题，由于多目标优化中的各个目标往往是相互冲突的，没有绝对最优解，只有满意解，多目标优化的最终解是一个解集，称为Pareto最优解，所有的最优解在空间的分布称为Pareto前沿.本文中采用Isight优化平台的NSGA-Ⅱ算法，它采用了快速非支配排序法，降低了计算复杂程度的同时保证了种群的多样性.

在Isight平台模拟的近似模型基础上添加优化模块，在模块中选定优化算法为NSGA-Ⅱ算法，分别进行垂荡与横摇、垂荡与纵摇、纵摇与横摇的优化计算，设置种群大小为100，种群代数为1 000代，交叉变异率为0.9，通过优化计算分析Pareto解集，该解集的上半部分区域为可行解，下半部分为不可行解，界面线为Pareto前沿，理论上Pareto前沿的解都是等价的，靠近Pareto前沿的解为最优解.

纵摇和横摇响应的Pareto解集见图7.在实际设计平台时由于不希望某个主尺度变量过于极端，因此在Pareto前沿上，可结合工程实际情况选取合适的Pareto解，该Pareto解即为多目标最优解.

深海半潜平台的纵摇与横摇往往是两个相互矛盾的目标，随着横摇的增大，纵摇往往在减小，选取图7中典型的A,B,C三点进行分析，三个点的各尺度数值及纵摇和横摇响应值见表3.从A点到B点纵摇响应下降了12.28%，而横摇响应上升了6.7%；B点到C点纵摇响应下降了10.4%，横摇响应上升了6.25%.在实际工程中，要综合考虑各主要尺度及响应状况选取合理可行的主尺度.

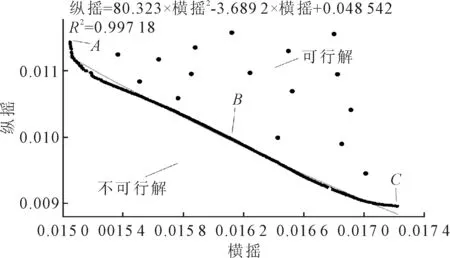
图7 纵摇与横摇优化Pareto解集

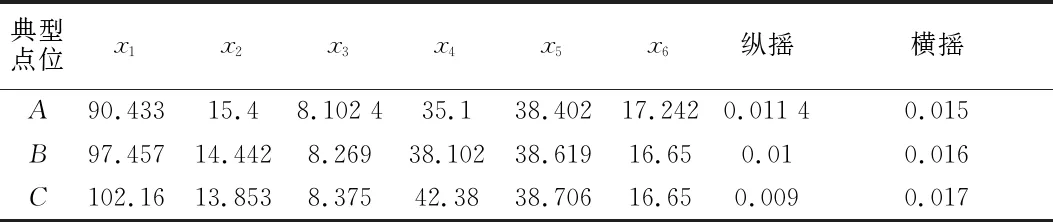
表3 纵摇与横摇响应Pareto前沿典型点

半潜平台的垂荡随着横摇的增加先减小再慢慢趋于平缓，其二者的Pareto解集见图8，同样选取典型三个点进行分析见表4.A点到B点垂荡响应下降了58.83%，横摇响应上升了6.57%，可见B点的综合性能要优于A点；B点到C点垂荡响应下降了6.87%，横摇响应上升了5.96%，幅度变化不大，因此在选取理想方案时可在B,C之间选取.

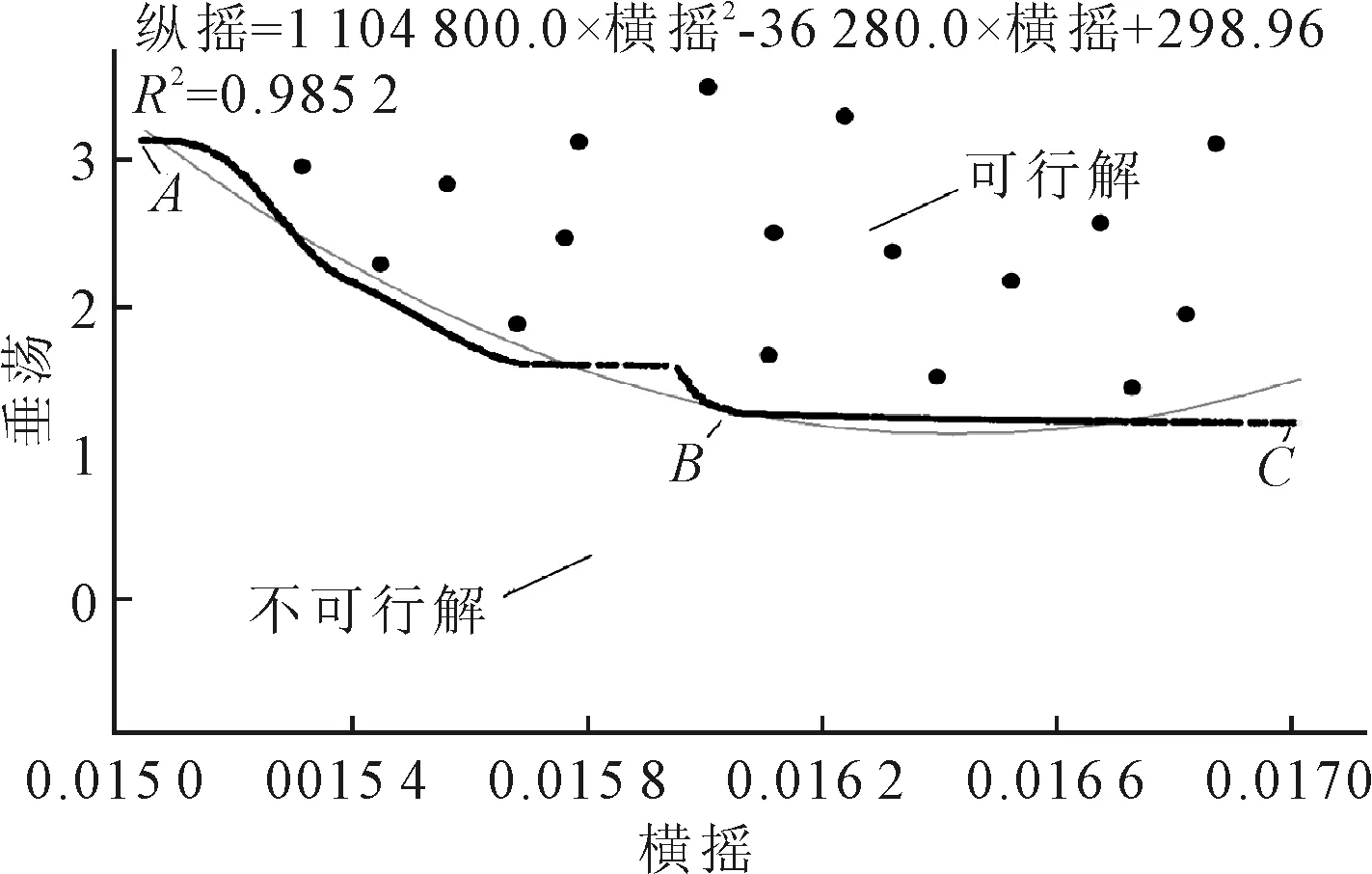
图8 垂荡与横摇优化Pareto解集

表4 垂荡与横摇响应Pareto前沿典型点

在纵摇响应较低时，垂荡响应随纵摇的增大急剧减小，当纵摇增加到一定程度后，垂荡响应变化趋于平缓，见图9，其中典型点见表5，A点到B点垂荡响应下降了70.5%，纵摇响应上升了3.05%，同样B点处的综合性能要优于A点；B点到C点垂荡响应下降了4.48%，横摇响应上升了5.13%，变化幅度很小，在考虑实际情况后可在B,C中间取理想方案.

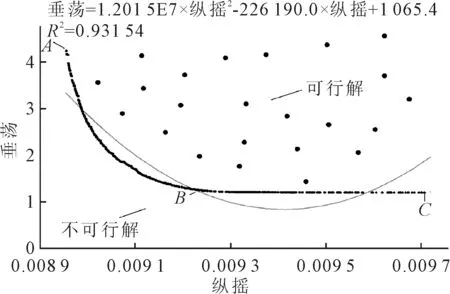
图9 垂荡与纵摇优化Pareto解集

表5 垂荡与纵摇响应Pareto前沿典型点

4 结 束 语

本文拟合了垂荡、纵摇和横摇响应与六个主尺度参数的关系，以初稳性高和排水量为约束条件，每两种运动响应为优化目标进行了多目标优化分析.通过试验设计在主尺度参数的变化范围内抽取200组方案，运用Seasam计算水动力性能，在Isight软件中采用径向基代理模型来拟合运动响应与主尺度参数的关系，通过R2来验证模型的精确度，基于拟合的近似模型采用NSGA-Ⅱ算法对每两种运动响应进行优化计算，得到了纵摇与横摇、垂荡与横摇、垂荡与纵摇的Pareto前沿，靠近Pareto前沿的主尺度方案为优化方案.