基于修正JC模型的船用Q345B钢动态本构研究*

罗 刚 谢 伟 李德聪

(中国舰船研究设计中心 武汉 430064)

0 引 言

对金属材料及结构在诸如爆炸、高速冲击等载荷作用下的塑性变形进行数值模拟时，最重要的问题是建立一个能真实反映材料响应过程中物理本质的本构模型[1].准确的本构关系对于数值仿真研究的重要性毋庸置疑[2].寻求一种适合于船用钢的动态力学本构模型对于船舶结构在遭受碰撞、爆炸等冲击载荷作用下的动响应数值分析一直是船舶结构领域的热点.

目前，在冲击动力学的数值计算方面，应用最广泛的金属材料本构方程[3]为Cowper-Symonds[4]材料模型(以下简称CS模型)及Johnson-Cook[5]材料模型(以下简称JC模型).其中CS本构模型建立了动态屈服应力与静态屈服应力的应变率函数关系，但未考虑动态屈服后流动应力的应变强化效应，其函数形式为

(1)

式中：σy为屈服应力；D和q为材料参数.

JC本构模型综合考虑了应变强化，应变率强化及温度软化，其本构模型方程是基于大量实验数据进行的拟合得到，而没有任何的物理证明[6].其具体形式为

(2)

式中各参数表示的物理意义及单位见表1.

表1 JC模型各参数物理意义及单位

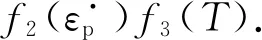
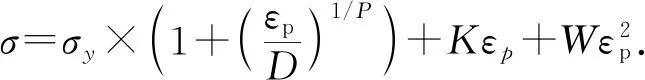
本文开展的主要工作为：①开展船用Q345B钢的准静态实验及SHPB实验获得了应变率在0.000 2 ～1 680 s-1范围内材料的应力-应变曲线；②依据实验结果和JC本构模型构造的一般思路，提出了Q345B动态本构模型的一般函数形式；③基于Q345B动态本构模型的一般函数形式，利用matlab拟合得到最佳的动态力学本构模型函数及其相关参数；④将本文拟合得到的Q345B动态本构模型与实验结果等进行了比较分析.

由于实验条件限制未开展不同温度下材料的本构模型试验，所以本文构造的动态本构模型不考虑温度影响.

1 船用Q345B钢力学性能实验

在常温(20 ℃)下开展准静态拉伸试验获得应变为0.002-1及1 s-1的应力-应变关系曲线.

本文针对船用Q345B钢采用的中等应变率实验为分离式霍普金森压杆(SHPB)开展，对于中应变率(102～104s-1)的测试，SHPB已经得到了普遍认可.SHPB实验的原理图见图1.

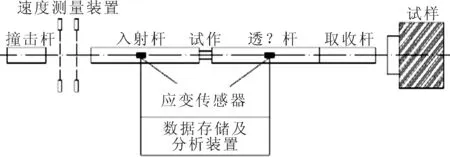
图1 SHPB实验装置原理图

利用一维应力假设和应力均匀性假设，得到时间的应力σ(t)，应变率ε′(t)和应变ε(t)，有：

(3)

采用该方法对Q345B钢分别开展了5组实验研究，每组实验3个试样，应变率从0.002～1 680 s-1，相应应变率下材料的本构关系曲线见图2a)，将后续应力随着硬板下降部分及弹性区域去掉后的本构关系图见图2b).各应变率下材料的屈服应力值见表2.

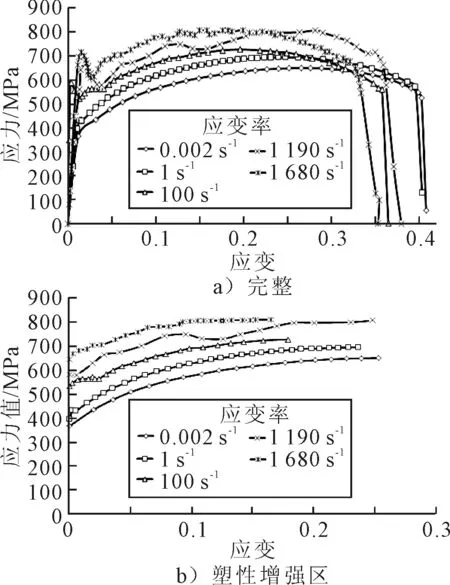
图2 Q345B钢应力-应变关系图

表2 不同应变率下Q345B的屈服应力性能

2 动态本构模型的构造

2.1 实验结果分析

将5组应变率下，应变分别为0～0.08下的4组数值下应力值提取出来见表3.

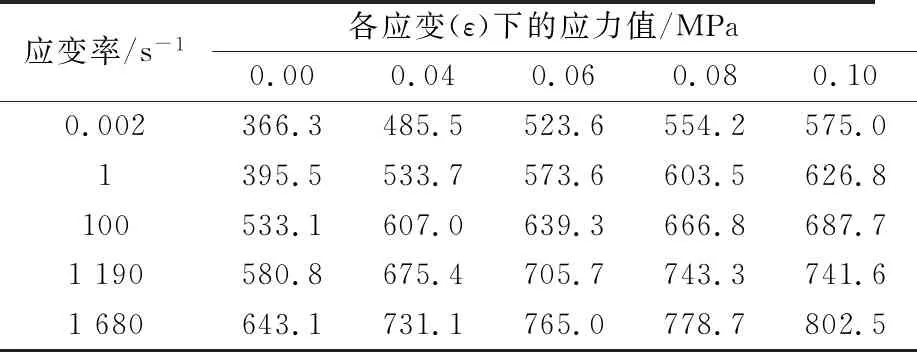
表3 不同应变率下4组应变值对应的屈服应力

Q345B的屈服应力与应变率间满足幂函数关系,见图3.

图3 Q345B钢屈服应力-应变率关系图

Q345B在0.04～0.10应变下塑性应力(总应力减屈服应力)与应变率间满足幂函数关系见图4.

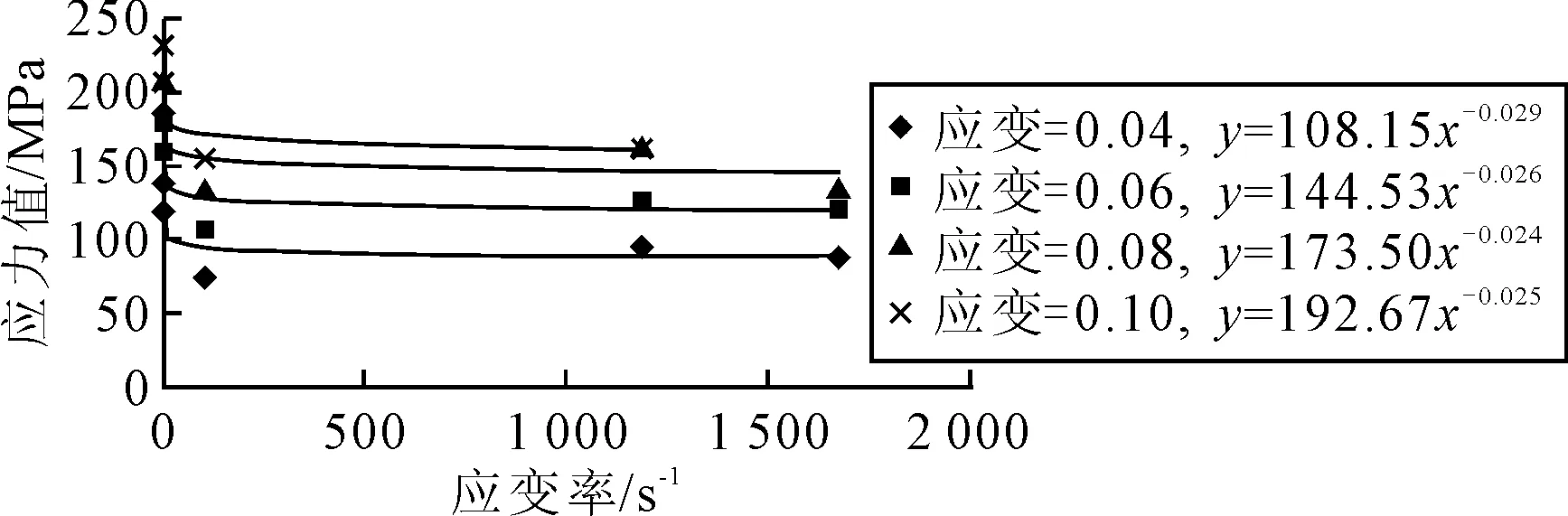
图4 Q345B钢流动应力-应变率关系图

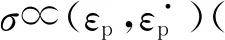
(4)

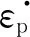
2.2 基于Matlab的材料模型及参数确定

基于上节给出的本构模型一般形式，引入初等函数(常数、幂函数)作为子项，采用Matlab最小二乘法开发程序确定函数关系及参数.程序的流程图见图5.

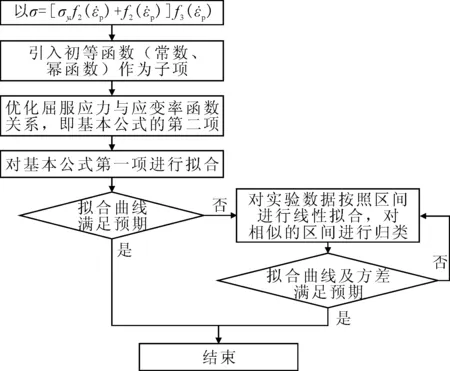
图5 基于Matlab的材料模型修正及参数确定的程序流程图

采用Matlab拟合得到的Q345B动态本构模型方程及相关参数为

式中:σy=366.3 MPa；k=0.14；b=1 096；m=0.50；c=-0.44；n=0.03.

3 实验结果分析

基于JC模型和文献[11]给出的公式，采用最小二乘法对图2的应力-应变本构关系曲线进行拟合，获得的本构模型函数关系及各参数分别见式(5)、式(6).

(5)

式中：σy=366.3 MPa；C=0.07；B=576.0；n=0.51.

(6)

式中：σy=366.3 MPa；D=7 339.00；P=4.41；K=1 028.00；W=3.76.

对上述各模型函数与实验值进行对比分析见图6.

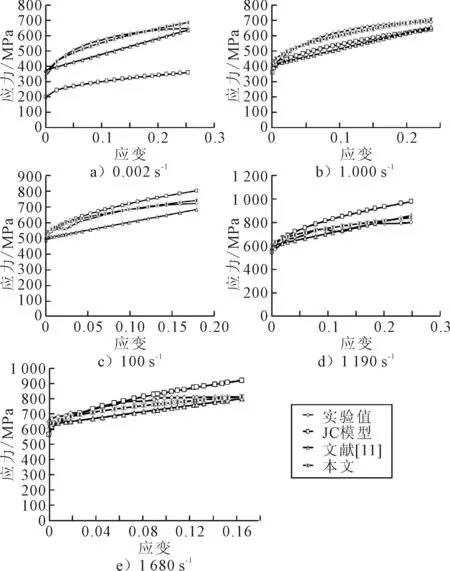
图6 不同应变率下Q345B本构模型对比分析图

各应变率下，三种动态本构模型方程与实验数据的数据分析见表4.其中:ζmax为最大误差值,%;|ζ|ave为误差绝对值的平均值,%.

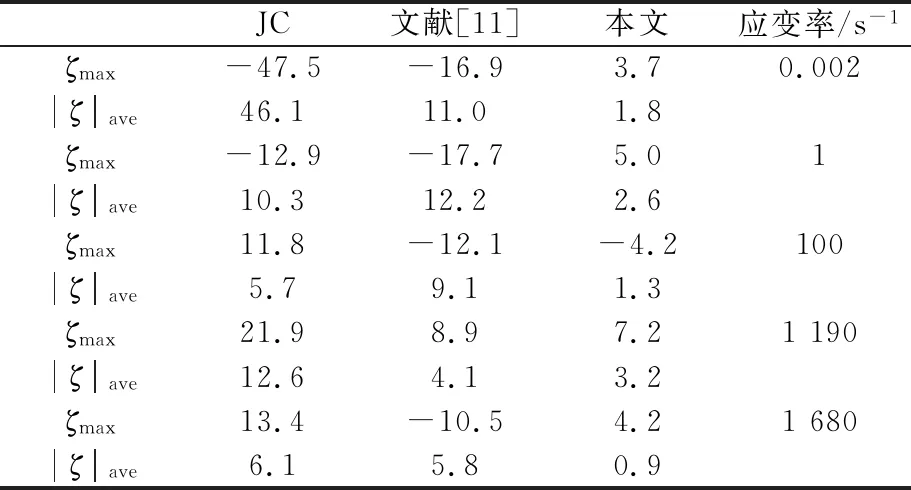
表4 各动态本构模型方程与实验数据误差分析

结果表明,本文给出的本构模型方程对于Q345B钢，从低应变率到中高应变率其应变-应变关系与实验数据均更吻合.

4 结 论

1) 对于船用Q345B钢，JC模型低估了应变率对屈服应力值的强化影响.

2) 假定流动应力区间应力-应变关系相似(JC/MJC/RJC)，或者假定流动应力区间，应力-应变关系完全相同.这述两种假定对于船用Q345B钢适用性较差.

3) 船用Q345B钢动态本构模型中，其动态屈服应力及应变强化项与应变率均为幂函数关系，但两者与应变率的函数关系有差异.