基于BAS-BPNN模型的季节性冻融期土壤含水率预测

李旭强，郑秀清，薛 静，陈军锋，陆帅帅

(太原理工大学水利科学与工程学院，太原 030024)

0 引 言

季节性冻融期土壤含水量对植被和作物生长以及区域生态系统均具有重要作用，准确预测冻融期土壤含水率对制定合理的春灌和春耕措施有重要的指导意义。学者从不同的视角对土壤含水率进行预测，最传统的方法是利用数理统计法、时间序列法等建立线性回归方程进行预测。但是由于土壤含水率具有复杂的非线性特征，是多因素相互受制，故而传统方法预测结果差异较大。目前，随着人工智能和大数据技术的迅速发展，一些新的预测方法应运而生，如机器学习[1,2]、遥感[3]等。作为机器学习的一类，BP神经网络(BPNN)大量应用于预测土壤含水率[4,5]，其具有强大非线性映射、高度泛化、自适应学习良好等能力，广泛应用于拟合。但是也存在容易陷入局部极小值、收敛速度慢、全局搜索能力弱等缺陷，因此，需要优化算法对传统的BPNN进行优化改进。遗传算法(GA)、粒子群算法(PSO)虽然能够有效地优化BPNN弥补缺陷，但其算法比较复杂，运算速度较慢。鉴于此，本文在利用主成分分析法筛选确定冻融期土壤含水率主要影响因子的基础上，基于天牛须搜索(BAS)对BPNN模型进行改进，建立了一种能够进行全局搜索、寻优速度快、运算量小、预测精度较高的BAS-BPNN模型，利用该模型对冻融期土壤含水率进行预测，并与其他同类模型进行比较分析。

1 材料与方法

1.1 试验区概况

试验区位于山西省晋中盆地太谷均衡实验站，海拔高程为773.0～783.0 m。属于典型的大陆性半干旱季风性气候，冬春多风少雨雪，降水主要集中在夏季，年平均降水量约415 mm，年水面蒸发约1 642 mm。试验于2016年11月22日至2017年3月15日进行，期间太阳总辐射为91.59 kJ/cm2，平均气温1.9 ℃，日最低气温为-16.0 ℃(1月19日)，总降水量为32.1 mm。

1.2 样本数据来源

试验站设有地面气象观测站，其主要观测项目为：太阳辐射I、地表土壤温度TS、气温TA、风速v、气压PA、相对湿度RH、降水P、水面蒸发量EW和土壤蒸发量ES。观测时段为每天8∶00、14∶00、20∶00。土壤温度、土壤含水率θ和土壤蒸发量样本值是以周为单位同步进行监测，监测时段8∶00-9∶00，共监测19组。土壤温度用预埋的热敏电阻传感器测定，土壤含水率采用取土烘干法测定；土壤蒸发量利用自制微型蒸发器监测。

气象观测站监测的7个因子取3次样本数据的平均值，而按周监测的θ、TS和ES三个因子的样本数偏少，直接进行建模训练与测试，预测结果达不到目标精度。因此，需要用插值法对θ、TS和ES三个因子内插生成114组日数据，以满足BAS-BPNN模型预测冻融期土壤含水率的要求。

1.3 理论方法

1.3.1 BP神经网络

误差反向传播多层前馈神经网络简称为BP神经网络(Back-Propagation Neural Network)[6]。BP网络由信号的前向传递与误差的反向传播两个过程组成，前向传递时，输入信号经各隐层逐层处理后，从输入层传向输出层。如果输出层的实际输出达不到期望的输出，则转入误差的反向传播，不断地调整网络的权值和阈值，使得训练网络达到预先设定精度要求或学习次数。

1.3.2 BAS算法原理

天牛须搜索(beetle antennae search, BAS)算法是在2017年提出的一种受天牛觅食原理启发的适用于函数优化的新智能算法。与果蝇算法、遗传算法、粒子群算法、灰狼算法等诸多智能优化算法相类似，但BAS算法在未知函数的具体形式和梯度信息的条件下即能自动寻求最优结果，可以大大提高运行效率。其仿生原理为：天牛是利用食物所散发出的气味强弱来觅食，而并不知道食物的具体位置。天牛利用两只触角，如果左边触角收到的气味强度大于右边触角收到的气味强度，则天牛下一步就会朝左边飞，相反则会朝右边飞[7]。其简化模型如图1所示。

图1 天牛须简化模型Fig.1 Beetle antennae simplified model

BAS算法建立数学模型的步骤如下：

(1)创立天牛须朝向的随机向量，并作归一化处理：

(1)

式中：rands()表示随机函数；m为空间维度。

(2)创立天牛左右须空间坐标：

(2)

式中：xrt、xlt分别表示天牛右须、左须在第t次迭代时位置坐标；xt表示天牛第t次迭代时质心坐标；d0表示两须之间间距。

(3)依照适应度函数f(x)判断左右两须收到的气味强度f(xl)和f(xr)的值。

(4)通过比较f(xl)和f(xr)的大小，进行迭代以更新天牛位置：

xt+1=xt-step·dir·sign[f(xrt)-f(xlt)]

(3)

式中：step表示第t次迭代时的步长因子；sign()为符号函数。

1.3.3 BAS-BPNN模型建立

为了更加精确快速的预测冻融期土壤含水率，在采用PCA对试验数据进行降维的基础上利用天牛须搜索算法优化BPNN的初始权值和阈值，并将其应用到已经设定好的BPNN中，从而构造出最终的BAS-BPNN预测模型。BAS-BPNN预测模型的流程如图2所示，具体建模步骤如下：

(1)选取的输入参数7个，输出参数1个，即输入层神经元个数为7，输出层神经元个数为1，隐含层神经元个数经多次训练确定为15，则模型结构为7-15-1。

(2)初始步长因子step选取可以尽量的大。计算迭代中变步长用式(4)：

stept+1=stept·eta(t=0,1,2,…,n)

(4)

式中：eta的值在[0,1]接近1，通常取eta=0.95。

(3)用模型输出值和实测值的均方误差MSE作适应度函数，函数表达式为：

(5)

式中：tsim(i)、Tsim(i)分别是第i个样本的模型期望输出值和实测值，N是输入样本数。

(4)随机数x=rand(k,1)作为天牛的初始位置保存于X中。

(5)按式(2)更新天牛左右须位置，并比较求出的左右两须的适应度函数值f(xl)、f(xr)大小，利用式(3)更新天牛位置，调整BPNN的权值和阈值。若适应度函数值优于Y，相应更新Y，X。

(6)若适应度函数值达到预设的精度0.001或是迭代的最大次数100次，转下一步骤，否则，返回步骤(5)继续迭代。

(7)当算法停止迭代时，X的值即为BPNN最优的初始权值和阈值。

(8)生成的最优解与通过主成分分析确定的样本值输入BPNN不断地训练并计算得到输出结果，利用MATLAB仿真图效果获得最佳模型，形成冻融期含水率预测模型。

图2 BAS-BPNN预测模型流程Fig.2 Flowing of BAS-BPNN forecasting model

1.3.4 模型精度评价指标

本文选取用决定系数R2和相对误差Ei来表征模型预测精度和性能优劣：

(6)

(7)

2 结果与分析

2.1 影响因子的分析与确定

冻融期土壤含水率影响因子作为BAS-BPNN模型的输入参数，即神经网络神经元个数，直接决定输入层到隐含层、隐含层到输出层的权值和阈值。土壤含水率与影响因子之间的关系体现在模型预测精度的高低上，因此，冻融期土壤含水率影响因子的详细分析和主要因子的选择是至关重要的。

冻融期该试验区剖面土壤含水率主要补给来源为降水或融雪水入渗，直接影响土壤含水率的大小。土壤含水率主要耗散方式为土壤蒸发，影响土壤蒸发的因子对土壤含水率产生间接影响。因此，除了直接影响土壤含水率变化的降水和蒸发两个因子外，还选取了影响土壤蒸发的因子：太阳辐射、气温、地表温度、风速、相对湿度、气压和水面蒸发。其中，太阳辐射、气温、降水量、风速受其他气象因子的影响较小，独立性较大；而地表温度、蒸发量、相对湿度、气压等很大程度上受以上4个因子的影响与制约。土壤冻融期，随着太阳辐射的不断降低，引起气温与地表温度的下降，导致土壤水分冻结从而引起土壤蒸发能力的降低，而土壤蒸发能力的变化对近地表土壤含水率产生直接影响。相对湿度较高，水汽接近饱和，增大大气压强，土壤蒸发减小，土壤就能长时间保持湿润[8]，相应的土壤含水率会升高且保持在一定的高含量水平。风速增大会促进蒸发，从而减小地表土壤含水率。

与冻融期土壤含水率有关的9个影响因子中，某些因子可能会对预测精度有不利影响或贡献极小，为了避免信息重叠，有必要筛选剔除这类因子，本文采用主成分分析法(PCA)选取对含水率影响较大的因子。利用SPSS软件得到的成分特征值及方差贡献率见表1，各主成分得分系数矩阵见表2。

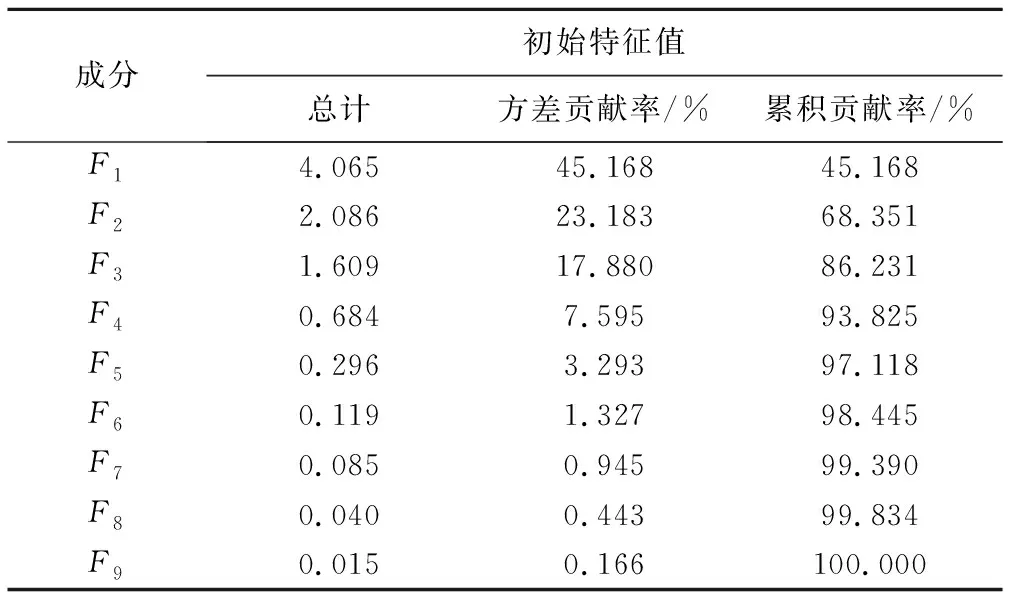
表1 成分特征值及方差贡献率Tab.1 Eigenvalue and variance contribution rate of principal component

由表1可知，前3个主成分特征值均大于1，且累积贡献率达86.231%(>85%)。故选取F1、F2、F3主成分替代原来9个指标的大部分信息。

表2 主成分得分系数矩阵Tab.2 Principal component score coefficient matrix

由表2可知，对于F1主成分得分系数较大的依次是I(0.251)、EW(0.245)、TS(0.229)、TA(0.225)，可以看成是反映太阳辐射、水面蒸发、地表温度、气温的含水率综合影响因子；对于主成分F2中ES(0.455)、P(0.451)和RH(0.166)得分系数较大，可看作是反映土壤蒸发、降水和相对湿度的含水率综合影响因子；主成分F3得分系数较大依次是v(0.524)、RH(-0.511)，可认为是反映风速和相对湿度的含水率综合影响因子。

主成分F1的方差贡献率为45.168%，对含水率的影响最大；主成分F2的占比为23.183%，对含水率的影响次之；而主成分F3只占17.880%，对含水率的影响最小。综上所述，将主成分F1和主成分F2看成是影响土壤含水率的主要部分，其主要影响因子分别是：太阳辐射、水面蒸发、地表温度、气温、土壤蒸发、降水和相对湿度。

2.2 模型参数选取

在MATLAB R2019a环境下，为了尽量消除输入参数的影响，使用了mapminmax 函数将样本数据进行归一化处理，范围为[-1,1]。运用附加动量法训练网络，训练函数为trainlm；网络学习率net.trainParam.lr=0.01；允许训练的最大次数net.trainParam.epochs=1 000；训练期望误差net.trainParam.goal=0.001。在监测到的114组样本数据中，选取94组作训练数据，其余20组作测试数据。训练达到指定精度时，得到优化后的权值和阈值，见表3所示。

表3 最优BPNN部分权值和阈值Tab.3 Decentralized value and threshold value of optimal BPNN

2.3 模型预测结果与讨论

本文以冻融期监测的114组冻融环境要素和地表土壤含水率为研究样本总体，从中随机选取94组样本作为训练集，剩余20组选作测试集，以MATLAB 2019a为平台，对模型进行验证。利用训练好的BAS-BPNN 含水率预测模型对2016年11月至2017年3月含水率进行预测，预测结果误差分析见表4。

表4 BAS-BPNN模型含水率预测训练与测试误差分析Tab.4 BAS-BPNN moisture prediction training and test error analysis

为了更加直观地观察预测结果，得到冻融期土壤含水率测试集预测值与实测值对比图，如图3所示。

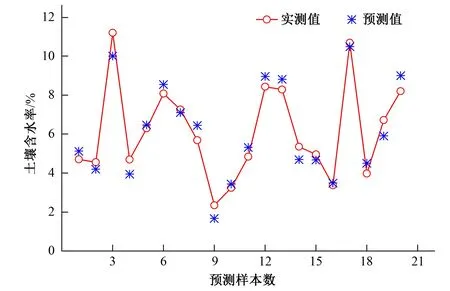
图3 BAS-BPNN模型含水率测试值预测Fig.3 BAS-BPNN water content test value prediction

由表4和图3可以看出，模型训练集平均相对误差为8.65%(小于允许误差20%)，决定系数为0.917 8；模型测试集平均相对误差为9.08%，决定系数为0.909 6，表明建立的BAS-BPNN模型有较高预测精度、较好性能，模型预测值与实测值有同样的变化幅度，相对误差也较小，模型预测曲线的走势非常逼近实测值。充分说明所建模型能够对冻融期土壤含水率进行有效的预测。

2.4 不同神经网络模型预测结果对比分析

为了检验BAS-BPNN预测模型与其他优化算法在冻融期土壤含水率方面的优越性，本文选择BPNN模型、GA-BPNN模型和PSO-BPNN模型从Ei和R2两方面与BAS-BPNN模型进行对比，结果见表5。同时，图4为4种模型最佳适应度变化曲线，对比其寻优和收敛速度。

表5 不同模型效果比较Tab.5 Comparison of different model effects

从表5可以看出，相较于BPNN，优化后的BAS-BPNN、PSO-BPNN、GA-BPNN模型都对原始数据有更好的预测。BAS-BPNN和PSO-BPNN模型的决定系数相接近但是要高于GA-BPNN模型的，BAS-BPNN模型的相对误差要远远小于PSO-BPNN和GA-BPNN模型，尤其是训练集相对误差。因此，从整体训练误差、测试误差以及决定系数分析，BAS-BPNN模型效果最佳，预测精度高，模型性能比较好，能够反映出BAS-BPNN模型在冻融期土壤含水率预测方面良好的适用性。

图4 不同模型最佳适应度曲线Fig.4 The fitness curve of different model

由图4可以看出，BAS-BPNN模型经过约10代即可找到最优解，而PSO-BPNN和GA-BPNN模型经过约40代，BPNN型甚至在经过近70代才找到最优解，说明BAS-BPNN模型寻优和收敛速度明显高于其他模型。

3 结 语

(1)利用主成分分析法筛选出对冻融期土壤含水率影响较大的7个因子：太阳辐射、水面蒸发、地表温度、气温、土壤蒸发、降水和相对湿度。

(2)BAS-BPNN模型训练预测值与实测值的决定系数为0.917 8，平均相对误差为8.65%；测试预测值与实测值的决定系数为0.909 6，平均相对误差为9.08%。BAS-BPNN模型寻优及收敛速度明显高于其他模型，从相对误差和决定系数两个指标分析，BAS-BPNN模型预测效果最佳表明模型可以较好地预测冻融期土壤含水率。

(3)BAS-BPNN模型是对冻融期土壤含水率进行预测的一种新的方法，为土壤含水率预测研究拓宽了思路。但也存在着不足，由于试验条件限制，样本数据时间频率精度较低，若用日变化尺度的模拟验证，会进一步提高预测精度。