滴灌施肥条件下土壤水分运移规律研究

2020-10-19魏小东胡朋成苏振娟

节水灌溉 2020年10期

魏小东，尹娟,2,3，胡朋成，苏振娟

(1.宁夏大学土木与水利工程学院，银川 750021；2.旱区现代农业水资源高效利用教育部工程中心，银川 750021；3.宁夏节水灌溉与水资源调控工程技术研究中心，银川 750021)

0 引言

滴灌作为新型的高效节水灌溉技术之一，在我国大部分地区已被广泛地应用[1-3]。研究表明，滴灌具有节水增产效果良好[4]，灌水均匀度高，对土壤结构损坏性小的特点，可有效防止土壤水产生深层渗漏和养料流失的现象，有效的降低土壤次生盐碱化的程度，最大化实现作物的经济效益[5，6]。

当下，我国在农业节水灌溉方面的技术日趋成熟，尤其对于滴灌技术的研究成果颇丰，并且做到了因地制宜[7]。宁夏作为我国旱区农业的主要发展地区之一，干旱缺雨、蒸发迅速、生态环境敏感复杂等问题是宁夏水资源供需过程的发展现状。由于我国节水灌溉农业的大力推进，根据自治区2018年水资源公报统计，全区已有高效节水灌溉面积23.53 万hm2，其中微灌面积占全区高效节水灌溉面积的70%以上，因此滴灌技术在宁夏地区也获得了蓬勃的发展。而枸杞作为宁夏重要的经济农作物，其滴灌种植技术的研究就成了许多学者青睐的课题，其中徐利岗等[8]以宁杞7号枸杞为研究对象，做了基于土壤水分下限的宁夏枸杞滴灌灌溉制度大田试验；程良等[9]通过开展枸杞覆膜与不覆膜滴灌田间试验，得出枸杞膜下滴灌技术适宜在宁夏中部干旱区广泛推广；赵彦波等[10]做了滴灌施肥条件下土壤湿润锋变化规律研究，为大田滴灌施肥系统设计提供参考依据；苏振娟等[11]利用土箱模拟进行了不同施N浓度下滴头流量对土壤水分运移的影响研究；吴军斌等[12]通过试验得出纵向土壤含水率的变化受滴头流量和氮肥浓度的影响，且滴头流量的影响程度更大，但是对土壤纵向或径向在0～30 cm范围内的土壤含水率随不同氮肥浓度的变化鲜有说明。本文针对滴灌对宁夏中部干旱带枸杞种植的影响，研究灰钙土(沙壤土)土壤含水率随再分布时间的变化过程、以及不同氮肥浓度对灰钙土土壤水分运移规律的影响，旨在比较系统的掌握滴灌施肥条件下枸杞田土壤水分的运移规律，为当地现代农业快速发展给予可靠的理论指导和技术支撑。

1 材料与设计

1.1 试验材料

试验设施主要由点源供水系统和点源入渗单元体(有机玻璃箱，规格：长60 cm、宽50 cm、高60 cm)组成，点源供水系统的工作原理为：马氏瓶来供应灌水和调控试验的准确度，橡胶软管代替滴头，具体装置如图1所示。由于滴灌入渗所形成的湿润体具有对称性，因此本试验选取滴灌形成湿润体的1/4作为试验对象，在试验时把滴头(橡胶软管)放置在土箱的直角处[13]。待滴头流量达到稳定后，开始试验并做好计时。

图1 试验装置示意图Fig.1 Schematic diagram of the test device

试验土壤取自宁夏中部干旱区吴忠市同心县下马关镇枸杞种植基地，土壤为灰钙土(沙壤土)。根据枸杞实际生长需要，计划湿润层深度设定为45 cm，等垂直湿润锋运移深度为40 cm时停止灌水。试验前将土壤自然风干、粉碎、过筛(2 mm)，依照设计容重分层装土，每5 cm一层，分9层，共45 cm(预留5 cm)，装土结束后让其自然沉降24 h以便获取均匀的初始含水率剖面。试验土壤的物理参数如表1所示、理化性质如表2所示。

表1 试验土壤物理参数Tab.1 Physical parameters of soil

表2 试验土壤理化性质 Tab.2 Physical and chemical properties of soil

1.2 试验设计

试验采用三因素完全随机组合设计，试验因素为：灌水量、滴头流量和氮肥浓度。灌水量设置3、5 L(W1、W2)2个水平；滴头流量设置0.50、0.75、1.00 L/h(q1、q2、q3)3个水平；氮肥浓度设置0、200、500 mg/L(F1、F2、F3)3个水平。共18个处理(T)，详见表3所示。

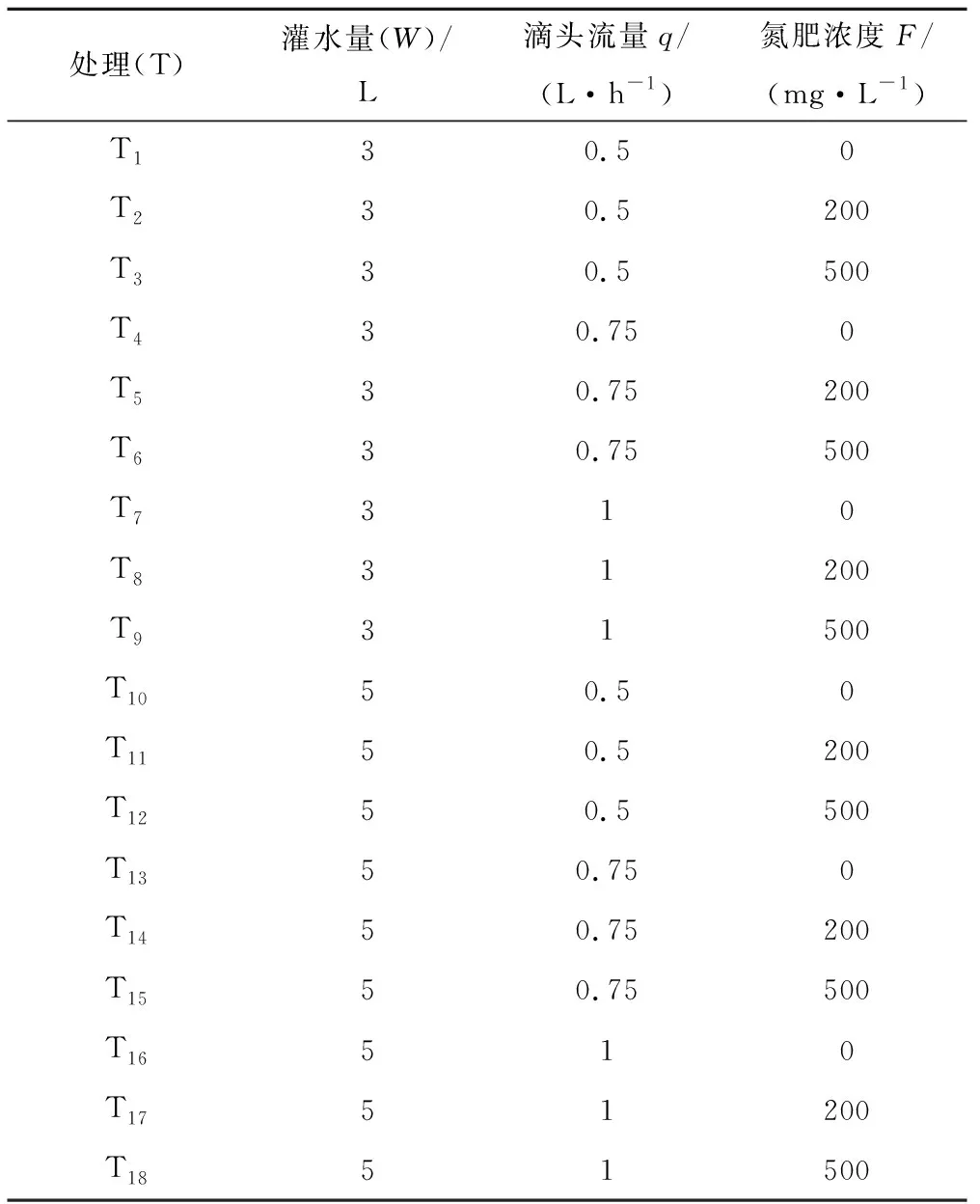
表3 试验设计Tab.3 Test design

滴水24 h后用直径为2 cm的土钻分层取土，取土间隔(纵向、径向)为5 cm，取土至未湿润土壤时终止。

采用烘干法测试土壤含水率(θ)。含水率测定的具体过程为，拟定在土箱边缘建立坐标，以滴头位置为原点，选取一定的角度(α)(0°、30°、45°、60°、90°)；水平径向距离(n，cm)；纵向土层深度(h，cm)；再分布时间(t，d)，设定为灌后：0 d(灌后立测)、1、3、5 d 4种；然后依次进行土壤含水率测定。

采用SPSS25软件进行数据处理，Origin 2017和Excel 2010软件进行图表绘制。

2 结果与分析

2.1 土壤含水率随再分布时间的变化规律

2.1.1 纵向土壤含水率随再分布时间的变化规律

图2表示同一滴头流量不同再分布时间下纵向土壤含水率变化过程。当滴头流量为q1(0.5 L/h)时，再分布时间0、1、3、5 d时湿润体含水率分别在28.79%～20.65%、17.99%～16.47%、15.48%～14.95%、14.2%～14.92%范围内，其土壤湿润体含水率差值分别为：8.14%、1.52%、0.53%、-0.72%。当滴头流量为q2(0.75 L/h)时，再分布时间0、1、3、5 d的湿润体含水率分别在30.95%～14.57%、19.47%～17.26%、15.9%～14.04%、14.66%～14.85%范围内，其湿润体含水率差值分别为：16.38%、2.21%、1.86%、-0.19%。当滴头流量为q3(1 L/h)时，再分布时间0、1、3、5 d湿润体含水率分别在30.77%～15.43%、19.93%～17.29%、15.98%～14.14%、14.61%～13.54%范围内，其湿润体含水率差值分别为：15.34%、2.64%、1.84%、1.07%。均表现为再分布时间越久湿润体纵向土壤含水率差值越小，当纵向土层深度h<25 cm时，表现为θt0>θt1>θt3>θt5，当纵向土层深度h>25 cm时，θt0的减小幅度最大。分析可得，在同一滴头流量不同再分布时间下，当再分布时间较短时(t<3 d)，土壤含水率随纵向土层深度的增加呈递减的趋势，且当再分布时间为0 d(灌后立测)时，土壤含水率减小得最快，其次是1、3、5 d。初步分析形成上述规律的原因主要为：土壤水分在垂向方向运移过程中，基质势和重力势为主要驱动力，再分布时间越短，土壤水分运移受重力势影响越强，土壤水分向下运动趋势越明显。这就说明同一滴头流量不同再分布时间下，土壤含水率随纵向土层深度的增加呈递减的趋势，但再分布时间愈久，湿润体表现为增大的趋势，相应的含水率范围扩大。

图2 同一滴头流量不同再分布时间土壤含水率纵向变化规律Fig.2 Longitudinal variation of soil moisture content at different redistribution times for the same droplet head discharge

采用SPSS进行纵向土层深度、再分布时间与土壤含水率的线性回归分析，结果如表4所示，由表可知再分布时间、纵向土层深度与土壤含水率之间呈极显著相关(p<0.01)，所形成的函数关系式为：

θ=25.173-1.908t-0.157h

由图3直方图、图4回归标准化残差正态P-P图可知，它们之间具有正态分布趋势，且拟合效果良好。

2.1.2 径向土壤含水率随再分布时间的变化规律

图5表示同一滴头流量不同再分布时间下径向土壤含水率变化过程。当滴头流量为q1(0.5 L/h)时，再分布时间0、1、3、5 d时湿润体含水率最大值与最小值的差值分别为：11.17%、4.74%、2.61%、1.43%。当滴头流量为q2(0.75 L/h)时，再分布时间0、1、3、5 d时湿润体含水率最大值与最小值的差值分别为：10.32%、5.45%、3.49%、1.95%。当滴头流量为q3(1 L/h)时，再分布时间0、1、3、5 d时湿润体含水率最大值与最小值的差值分别为：13.15%、6.37%、4.33%、1.94%。均表现为再分布时间越久径向土壤湿润体含水率最大值与最小值的差值越小，当水平径向距离n<25 cm时，表现为θt0>θt1>θt3>θt5，当水平径向距离n>25 cm时，θti大小顺序会发生小幅度变化，但总体趋势变化不大。这就说明，在同一滴头流量不同再分布时间下，土壤含水率随水平径向距离的增加呈递减的趋势，且当再分布时间为0 d(灌后立测)时，在水平径向距离0～30 cm内土壤含水率均减小得很快，而当再分布时间为1、3、5 d时，土壤含水率减小得相对平缓。初步分析形成上述规律的原因主要为：滴灌入渗过程中，水势梯度是影响水分向四周运移的关键要素，当离滴头越远，基质势和土壤的吸附能力则会越弱，对应的湿润体含水率就会越小。说明在同一滴头流量不同再分布时间下，土壤含水率与水平径向距离呈负相关关系，再分布时间越久土壤含水率减小得越平缓，但是当水平径向距离超过25 cm时，θti相较其他水平径向距离土壤含水率下降得较快。

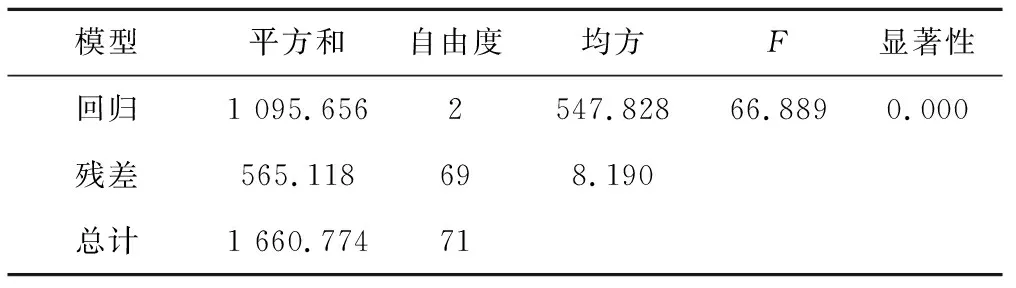
表4 土层深度(0～30 cm)和再分布时间对于含水率总体方差分析Tab.4 Total variance analysis of soil depth (0～30 cm) and redistribution time for water content

图3 直方图Fig.3 Histogram

图4 回归标准化残差正态P-P图Fig.4 Regression normalized residual normal P-P diagram

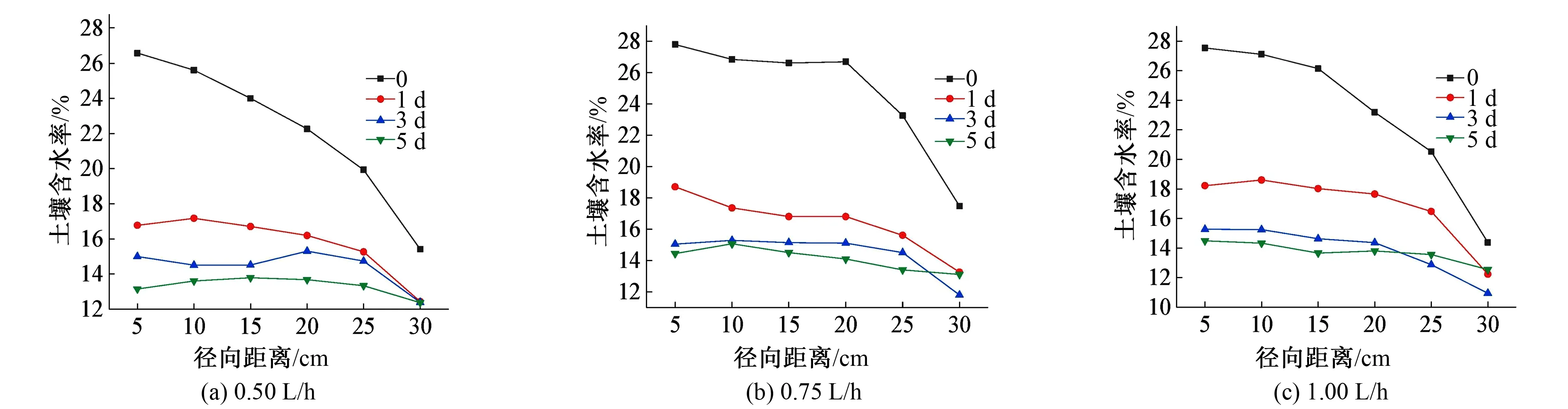
图5 同一滴头流量不同再分布时间土壤含水率径向变化规律Fig.5 Radial variation law of soil moisture content at different redistribution time of the same droplet head discharge

采用SPSS软件进行水平径向距离、再分布时间与土壤含水率的线性回归分析，结果如表5所示，由表可知再分布时间、水平径向距离与土壤含水率之间呈极显著相关(p<0.01)，所形成的函数关系式为：

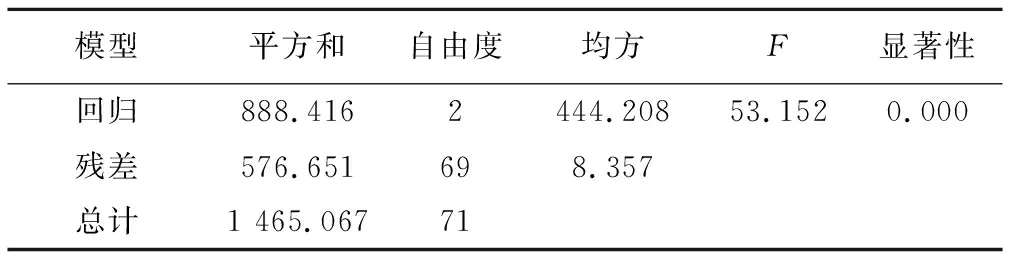
θ=23.884-1.597 t-0.201 n

由图6直方图、图7回归标准化残差正态P-P图可知，它们之间具有正态分布趋势，且拟合效果良好。

图6 直方图Fig.6 Histogram

2.2 土壤含水率随氮肥浓度的变化规律

2.2.1 纵向土壤含水率随氮肥浓度的变化规律

图8表示同一滴头流量不同氮肥浓度下纵向土壤含水率变化过程。当滴头流量为q1(0.5 L/h)时，氮肥浓度0、200、500 mg/L时土壤湿润体含水率分别在21.3%～6.95%、19.41%～7.24%、17.74%～7.12%范围内，其湿润体含水率差值分别为：14.35%、12.17%、10.62%，随氮肥浓度增大呈递减趋势，纵向土层深度h<25 cm时，表现为θF2>θF1>θF3，纵向土层深度h>25 cm时，θF2急剧减小，不再是最大值。当滴头流量为q2(0.75 L/h)时，氮肥浓度0、200、500 mg/L时湿润体含水率分别在16.78%～12.6%、18.58%～5.35%、16.85%～8.06%范围内，其湿润体含水率差值分别为：4.18%、13.23%、8.79%，出现较大幅度波动，纵向土层深度h<25 cm时，表现为θF2>θF3>θF1，纵向土层深度h>25 cm时，θF2急剧减小，表现为θF1>θF3>θF2。当滴头流量为q3(1 L/h)时，氮肥浓度0、200、500 mg/L时湿润体含水率分别在17.05%～15.43%、17.9%～14.41%、16.59%～14.22%范围内，其湿润体含水率差值分别为：1.62%、3.49%、2.37%，出现小幅度波动，纵向土层深度h<25 cm时，表现为θF2>θF1>θF3，纵向土层深度h>25 cm时，θF2同样迅速减小，但相比滴头流量为q1、q2时q3情况下的θFi减小得又相对平缓。由此可以得出，在同一滴头流量不同氮肥浓度下，土壤含水率随纵向土层深度的增加有一定幅度的波动，但是总体呈递减的趋势。初步分析形成上述规律的原因主要为：由土壤水分特征曲线表明，土壤吸力(负压)随土壤水分的增大而减小。随着氮肥浓度的增大，土壤溶质势变大，土壤吸力就会越大，则纵向土壤含水率就会减小，这就说明在同一滴头流量不同氮肥浓度下，土壤含水率与纵向土层深度呈负相关关系，当纵向土层深度小于25 cm时，θF2均为最大值，而当纵向土层深度大于25 cm时，θF2急剧减小，不再是最大值，且在同一纵向土层深度不同氮肥浓度处理下的土壤含水率最大差值为7.25%(>5%)，说明氮肥浓度的变化对纵向土壤含水率有较大的影响，由表6可知，氮肥浓度、纵向土层深度与土壤含水率之间呈极显著相关(p<0.01)，且所形成的函数关系式为：

图8 同一滴头流量不同氮肥浓度土壤含水率纵向变化规律Fig.8 Longitudinal change rules of soil water content with different nitrogen fertilizer concentrations in the same droplet discharge

θ=20.688-0.256F-0.002h

2.2.2 径向土壤含水率随氮肥浓度的变化规律

图9表示同一滴头流量不同氮肥浓度下径向土壤含水率变化过程。当滴头流量为q1(0.5 L/h)时，氮肥浓度0、200、500

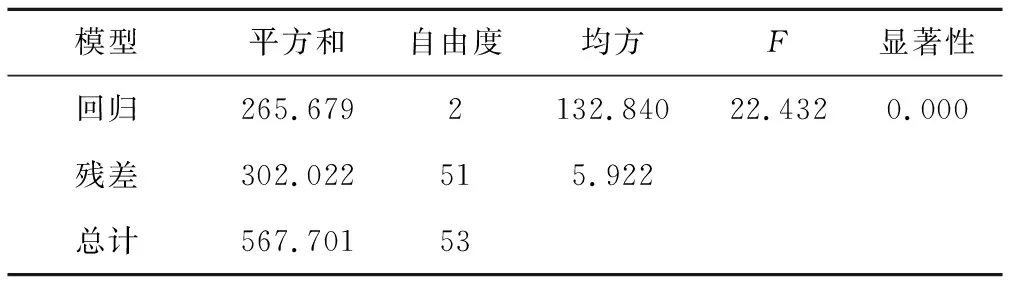
表6 土层深度(0～30 cm)和氮肥浓度对于含水率总体方差分析Tab.6 Total variance analysis of soil depth (0～30 cm) and nitrogen fertilizer concentration for water content

mg/L时土壤湿润体含水率最大值与最小值的差值分别为7.16%、6.76%、6.87%，出现小幅度波动；当滴头流量为q2(0.75 L/h)时，氮肥浓度0、200、500 mg/L时湿润体含水率最大值与最小值的差值分别为7.07%、6.8%、5.31%，呈依次递减的趋势，显然在滴头流量为q1、q2时，水平径向距离n在0～30 cm范围内均表现为θF1>θF2>θF3，当水平径向距离n<25 cm时，θ均匀减小，当水平径向距离n>25 cm时，θ减小得较快。当滴头流量为q3(1 L/h)时，氮肥浓度0、200、500 mg/L时湿润体含水率最大值与最小值的差值分别为5.82%、4.21%、3.81%，呈依次递减的趋势，水平径向距离n<25 cm时，均表现为θF1>θF2>θF3，水平径向距离n>25 cm时，θF1比θF2、θF3都减小得迅速，且大小顺序也有小幅度的变化，但不会形成多大的影响。通过分析说明，在同一滴头流量不同氮肥浓度下，土壤含水率随水平径向距离的增加呈递减的趋势，水平径向距离为25 cm是土壤含水率减小的关键节点，水平径向距离大于25 cm时，θFi减小得更快，但在同一水平径向距离不同氮肥浓度处理下的土壤含水率最大差值为3.65%(<5%)，说明氮肥浓度的变化对水平径向土壤含水率的大小没有显著影响，通过线性分析，建立氮肥浓度、水平径向距离与土壤含水率之间的函数关系式为：

θ=20.492-0.205F-0.002n

综上分析，在研究非饱和土壤水分运移过程中一般不考虑有关土壤水分的影响,而是把重力势和基质势作为研究重点。

图9 同一滴头流量不同氮肥浓度土壤含水率径向变化规律Fig.9 Radial variation rule of soil moisture content with different nitrogen fertilizer concentrations in the same droplet discharge

3 讨论

研究得出：再分布时间与纵向土壤含水率的拟合效果优于再分布时间与径向土壤含水率的拟合效果，相关性前者也更好。但是目前在宁夏中部干旱区枸杞滴灌种植试验中进行再分布时间与土壤含水率的相关研究较少，是否存在这样的相关性还有待验证，在今后的试验中将利用Hydrus并结合数学模型的方式对该部分内容做进一步的研究。

此外，试验表明：在同一纵向土层深度或水平径向距离下，氮肥浓度的变化对纵向土壤含水率的影响较大，对径向土壤含水率的影响较小，这与吴军斌等[12]在滴灌施肥条件下土壤水分的运移规律的研究和李文[14]有关变浓度条件下土壤水分含量分布规律的研究规律相似，因此施肥浓度对纵向土壤水分运移的影响是不能忽视的。

4 结论

通过室内点源滴灌模拟试验，分析土壤水分运移过程的规律可得出以下结论。

(1)在同一滴头流量不同再分布时间下，当再分布时间较短时(t<3 d)，土壤含水率随纵向土层深度的增大呈递减的趋势；同一滴头流量不同再分布时间下，土壤含水率随水平径向距离的增大呈递减的趋势；且均表现为正态分布，拟合效果良好。纵向土层深度或水平径向距离超过25 cm时，各再分布时间下的土壤含水率减小得更快。