深基坑钢支撑预加力对围护墙变形影响
2020-10-19曹雪山额力素曹怀玉
曹雪山,额力素*,曹怀玉
(1.河海大学 道路与铁道研究所,江苏 南京 210098;2. 河海大学 环境学院,江苏 南京 100084)
随着地铁建设的快速发展,基坑开挖所引起的变形问题愈发引起工程界的关注。由于城市内复杂的周边环境对基坑变形要求严格,基坑开挖设计必须从传统的强度控制设计向以位移控制设计方向转变,这就要求对现有工程技术措施展开更为深入的研究[1]。
钢支撑预加力技术对基坑变形具有重要影响。Terzaghi[2]在研究基坑工程中的岩土工程问题时提出了预估开挖稳定程度和支撑荷载大小的总应力法。Mana和Clough[3]利用有限元方法,分析了支撑预加力对支护结构变形的影响,指出在支撑两端施加预力可以有效地减少基坑支护结构变形。Clough和Tsui[4]通过有限元研究了支撑预加力数值、墙体刚度、开挖深度等因素对围护墙性能的影响,发现当预加力为 0.2~0.4 倍的静土压力时,围护墙位移量可比无预加力时减小 50%以上,由此提出合理选择参数,可以显著地减少墙体位移和周围土体的沉降。洪德海[5]分析了预加力的作用和工程实际中围护墙变形过大的原因,并通过实例分析证明了施加合适的预加力,可有效减少围护墙变形。曹雪山等[6]认为土体变形过大后会导致土体强度参数减小。
钢支撑预加力不足的现象很普遍。《上海市基坑工程设计规程》(DG/TJ08—61—2010)[7]规定,钢支撑预加力控制值应为支撑轴力设计值的50%~80%;并强调预加力可检验支撑连接结点的可靠性。《建筑基坑支护技术规程》(JGJ 120—2012)[8]规定钢支撑预加力控制值取轴向压力标准值的50%~70%。可见规程不同,对钢支撑预加力值控制值的基准也不同。《建筑基坑工程监测技术规范》(GB 50497—2009)[9]规定一级基坑的轴力预警值取构件承载能力的60%~70%,但没有给出构件承载能力的参考值或计算方法。《江苏省城市轨道交通工程监测规程》(DGJ 32/J195—2015)[10]规定一级基坑的轴力控制值取支撑轴力设计值的60%~70%,并提出预警等级,黄色预警值为控制值的80%。虽然确定轴力控制值的参考标准不同,但都提出了支撑预加力值控制值的指标。与基坑的其他测项,如变形、水位等的预警理解思路相同,当轴力实测值小于轴力设计值的48%~56%是安全的,不存在危险信号。设计人员从规范出发,通常建议预加力值为低值,如取40%的支撑轴力设计值,以达到施加预加力后轴力值不大于预警值的目的。施工过程中参建各方也遵从规范和设计要求,认为轴力值宜小不能大,钢支撑施加的预加力达不到设计建议值,仍符合规范和设计要求。这说明在工程中对钢支撑预加力作用的认识是极其模糊的,这也是造成实际工程中钢支撑预加力普遍不足的一个重要原因。
综上,虽然学术界已经明确了钢支撑预加力对基坑变形具有显著的控制效果,但由于国家标准、规范、规程条文规定有差别,以及工程界对条文理解差异,导致预加力施加严重不足,进而大大削弱了钢支撑的作用效果。为此,本文以南京某地铁车站深基坑开挖工程为例,应用Midas GTS 软件数值分析,进一步分析了钢支撑预加力对围护墙变形的影响,明确了钢支撑预加力的意义,提出了钢支撑轴力双向预警、预加力比值确定方法,为类似工程提供参考。
1 工程概况及钢支撑预加力施加意义
1.1 工程概况
某地铁车站基坑总长179.3 m,车站中部标准段基坑宽20.9 m,深度17.908 m,支护结构采用800 mm厚地下连续墙加内支撑的结构形式,地连墙深度33.5 m,标准段共设四道支撑,第一道混凝土撑,截面尺寸为1 000×1 200 mm,间距为9 m;第二—第四道采用φ609,t=16 mm规格的钢支撑,间距为3 m。

图1 基坑标准段剖面图
1.2 预加力施加的工程意义
实际预加力明显低于设计预加力。图2为该基坑各断面钢支撑预加力实测值。三层钢支撑,每层5个共15个预加力实测数据,仅有一个实测预加力达到设计预加力。表1为实测预加力与设计预加力的百分比。表1中平均值为39%,且以小于40%居多。李书银[11]报道了昆明地铁4号大唐子站标准段与扩大段的钢支撑预加力数据统计,扩大段为设计预加力的5%~69%,以小于30%的居多;标准段为22%~56%之间,其中以小于40%的居多。这说明实际预加力不足的现象已经成为工程常态。
实际预加力不足的本质是工程技术指标不达标。由现有工程技术水平较低或复杂地质条件等原因造成了钢围檩与围护墙面存在不整合缝隙,例如对鼓包、凹凸不平的地连墙或桩墙平整度处理不够,钢支撑端部钢板变形、扭曲等。工程施工过程中,通常对不显著的不整合缝隙工况直接架设,否则加塞钢楔子,填筑水泥砂浆、水泥加部分细骨料,加入适量早强剂或提高填料的强度等级,以能在较短时间内达到理想强度,达到填塞不整合缝隙的目的。但实际上效果并不理想[11],表现为预加力损失仍显著。
预加力的工程意义在于能克服钢支撑理论抗压刚度小的缺点。钢支撑、钢围檩、围护墙之间连接紧密、无间隙时,力的产生机理与混凝土支撑相同。混凝土支撑,由于截面积大,相应的理论抗压刚度EA就大。本基坑的混凝土支撑抗压刚度为3.78×1010N,而钢支撑抗压刚度为5.96×109N,前者是后者的6.34倍。设计轴力接近2 000 kN,支撑长度取基坑宽度20.9 m,则混凝土支撑轴向压缩量为1.15 mm,而钢支撑为7.28 mm。钢支撑压缩量大的根本原因是其理论抗压刚度小。设计方案中钢支撑的水平间距3 m,混凝土支撑间距9 m,似乎具有通过增加支撑密度弥补钢支撑抗压刚度不足的目的,其实还不够。但是如果预加力达到2 000 kN,则钢支撑无压缩量;混凝土支撑因无法施加预加力,压缩变形不可避免,于是预加力技术间接地增大了钢支撑的理论抗压刚度。
预加力技术还能提高钢支撑的实际抗压刚度。理论的支撑压缩量表现为围护墙向坑内的变形量。在实际施工过程中,洪德海[5]观测到围护墙变形约18~35 mm,同时发现钢围檩与围护墙之间存在缝隙5 ~10 mm,认为两者关系密切。钢围檩与围护墙之间缝隙不可避免,通常加塞钢楔子或不作处理等不规范的处理方法是造成预加力大幅度损失显著的主要原因。规范的做法是在钢围檩背后适量加塞钢板,但也不可能达到理想状态。因此钢支撑的实际抗压刚度要明显小于理论值。检测实际预加力值是否满足要求是评价钢支撑架设质量的重要手段。在轴力值从无到设计值的变化过程中,低轴力值的支撑连接结点可靠性不能等同于高轴力值的可靠状况,因此在施加预加力时,有必要检测设计轴力值时支撑连接结点可靠性[7]。

图2 钢支撑预加力实测值
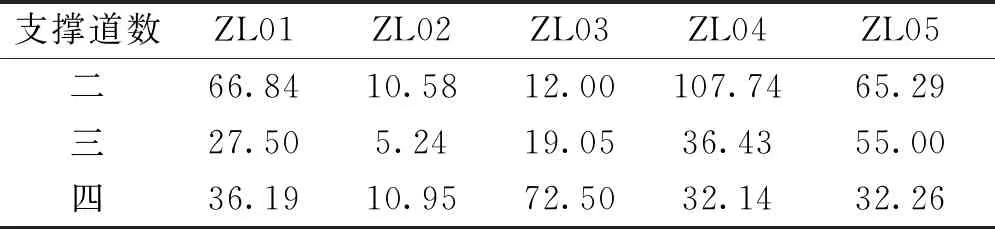
表1 各断面钢支撑预加力施加率情况(单位:%)
2 有限元数值模拟方法
2.1 模型建立
利用岩土和隧道工程有限元分析软件Midas GTS,模拟基坑工程开挖过程,研究预加力对基坑变形的影响。模拟计算中,选取修正摩尔-库伦模型的土体本构关系,支撑及围护桩采用线弹性模型;计算范围为可能影响区,即基坑周边2.0~3.0倍开挖深度,即62 m,深度为50 m,约为开挖深度的3倍。因基坑为轴对称的,如图3所示为半个基坑。

图3 模拟计算剖面有限元模型
2.2 模型参数及施工阶段模拟
模型参数取自场地的地质勘察报告及施工方案,通过场地岩土勘察及现场取样,分析室内试验数据所得。具体岩土参数及基坑支护结构详见表2、表3。
模型建立完成后,根据施工方案所确定的分层开挖顺序进行分步模拟,主要有初始状态的初始应力,位移归零;接着围护墙施工,然后分层开挖;每层土开挖后,架设圈梁或钢围檩和支撑,最后一层开挖后完成垫层及底板。

表2 土体物理力学参数

表3 支护结构构件计算参数
2.3 计算模型适用性验证
图4为基坑标准段断面ZL03处基坑围护墙水平位移计算值与实测值对比图。由于围护墙内测斜管底部未进入稳定岩土体,管口墙顶位置为钢筋混凝土支撑,结构刚度大,变形小,可近似作为固定零位移起算点。从图4可知,深层水平位移曲线呈现“鼓肚形”的抛物线状,计算值与实测值总体趋势一致,数值相当。当基坑土方开挖至基底时,深层水平位移的最大值及其位置深度的实测值与计算值对比如表4所示,最大位移偏差为6.4%,深度位置偏差为11.1%。钢支撑轴力实测值与计算值对比如表5。钢支撑在第二道处的支撑轴力相对误差最小,仅有8.1%,第四道其次,第三道最大,为27.5%。
综上,模型计算值与实测值吻合较好,验证了计算模型及计算参数的适用性,可进一步采用本模型及参数分析钢支撑预加力对基坑围护墙变形、支撑轴力最终值的影响。

表4 围护墙深层水平位移最大值的实测值与计算值比较

表5 钢支撑轴力实测值与计算值对比

图4 围护墙深层水平位移计算值与实测值对比
3 预加力施加效果研究
3.1 预加力施加方案
为了能模拟分析不同预加力值对围护墙深层水平位移、最终支撑轴力的影响,考虑钢支撑预加力阈值的5 种工况:实际预加力值(即实测初始轴力值),设计预加力值,规范控制低值、规范控制高值及轴力设计值等,具体计算方案如表6所示。
本基坑的钢支撑预加力实测平均值为设计预加力值的39%,考虑文献资料[11]以及计算方便性,实测预加力值为设计预加力值的40%;同时在本基坑的设计预加力值为设计轴力值的40%,于是实测预加力值为支撑轴力设计值的16%。如果定义预加力比值αpd为支撑轴力预加力值与设计值f之比所计算的数值,即
(1)
式中,f为支撑轴力设计值;fy为支撑轴力预加力值。于是实测预加力比值αpd为0.16。
相应地《江苏省城市轨道交通工程监测规程》(DGJ 32/J195—2015)[10]规定一级基坑的轴力控制值取支撑轴力设计值的60%~70%,则取规范控制低值、规范控制高值时预加力比值αpd分别为0.60和0.70。

表6 钢支撑预加力值计算方案(单位:kN)
3.2 预加力对围护墙深层水平位移的影响
图5为支撑轴力预加力比值αpd不同时,不同深度处围护墙深层水平位移值。很明显,随着预加力比值αpd愈大,即表示预加力愈大,深层水平位移最大值愈小。

图5 不同钢支撑预加力比值时围护墙水平位移
图6展示了不同的钢支撑预加力比值αpd时,围护墙深层水平位移最大位移值及其位置变化趋势。总体趋势是预加力比值αpd与围护墙深层水平位移最大值成很好的线性关系,其相关度R2达到0.999 8;而与最大位移发生的位置深度的线性关系明显降低,其相关度R2达到0.864 7,这与模型验证时最大位移值及位置的相对误差相对应。
预加力愈大,相应的围护墙深层水平位移最大值愈小的关系与目前文献研究成果[3-5]相一致,再一次证明了加大钢支撑预加力可减小基坑变形的作用。

图6 围护墙深层水平位移最大位移值及其位置与预加力比值αpd的关系
3.3 预加力对支撑轴力最终值的影响
图7展示了不同的钢支撑预加力比值αpd时,不同深度支撑的最终支撑轴力值变化趋势。总体趋势是随着预加力比值αpd增大,第二、第三道支撑轴力最终值呈现线性减小趋势,而第四道支撑轴力最终值呈现线性增大趋势;支撑轴力最终值变化趋势明显小于轴力预加值变化趋势。这与洪德海[5]关于预加力与支撑轴力最终值的影响不明显的结论相验证。

图7 不同深度钢支撑的最终支撑轴力值、预加力值与预加力比值αpd的关系
设计文件中,每道支撑的轴力设计值是不同,故定义轴力最终比值αld为支撑轴力最终值与设计值之比所计算的数值,即
(2)
式中,fl为支撑轴力最终值。αld作为支撑轴力最终相对值,避免了绝对值的差异影响。αld计算结果及其统计值如表7所示。支撑轴力最终比值αld的变化趋势同于支撑轴力的最终值。本例中该比值αld对第二道是最大,均值达0.68;第三道最小,均值达0.33;,第四道介于中间。随着预加力值比值αpd增大,最终轴力比值αld均值虽有增长趋势,但基本处于平稳状态。

表7 不同预加力比值αpd下的轴力最终值与设计值的比值αld统计表
3.4 预加力施加效果分析
钢支撑预加力就是一开始作用在支撑内的轴力,给围护墙提供坑内侧向作用力。在基坑分层开挖过程中,坑内土压力随开挖深度而变化,支撑轴力、坑外土压力、围护墙内力等与围护墙变形发生耦合而相互变化,因此围护墙的平衡状态是动态。
定义预加力贡献度αyl为支撑轴力预加力值与最终值之比所计算的数值,即
(3)
αyl反映了支撑轴力预加力值在基坑开挖施工过程中对支撑轴力最终值贡献度。αyl计算结果及其统计值如表8所示。当αyl小于100%表示预加力值不足,在基坑分层开挖过程中,墙体向坑内变形压缩支撑,增补了轴力最终值的其余部分,相应地墙外土体向墙也有位移,土压力更接近了主动土压力值。相反,当αyl大于100%表示预加力值充足,在基坑分层开挖过程中,墙体具有向坑外变形趋势,释放支撑轴力,同时墙向外挤压土体,土压力向被动土压力转变。
如表8所示,当αpd为0.16时,如基坑施工中预加力现状,预加力不足,增大围护墙向坑内变形和地表变形值,这种现象在软土基坑显现更为明显。若参建各方重视预加力,严格执行设计所给的预加力值,即保证了αpd为0.40时,则本例的基坑支撑轴力预加力经济性最佳,支撑轴力平均值更接近最终值,总体上支撑轴力达到了基本稳定状态。若αpd为0.60~0.8时,本例的第二道支撑轴力预加力更接近最终值,而平均值稍高于最终值。在预加力值取设计轴力值时,即αpd为1.00时,本例的所有支撑轴力预加力值均大大超过了最终值,所以预加力的经济性最差。

表8 支撑预加力与最终值的比值统计分析表
4 讨论
基坑工程的支撑轴力是一个特殊的测项。国内针对基坑工程设计与施工的国家规范、行业及地方规程[7-10]对支撑轴力均有控制值的规定,按照基坑工程的多数测项,如基坑周边地表沉降、建筑沉降与水平位移、围护墙顶水平位移、垂直位移,以及水位等,当测试值小于控制值,可以认为基坑安全可控,而大于控制值,则表示基坑安全不可控。这是工程界、学术界等共同认可的。然而,支撑轴力与这些测项不同。支撑轴力是保证围护墙处于动态平衡状态一个重要因素。没有支撑轴力,围护墙的位移将显著增大[4]。因此片面地将支撑轴力与其他测项等同化理解是不合适的。
正确理解支撑轴力设计值、最终值及预加力值。以本文的基坑为例,尽管设计文件已经有了确定的支撑轴力设计值,但数值计算结果显示支撑轴力设计值还不一定是轴力最终值。支撑轴力最终值还与预加力值相关。支撑轴力预加力值较小时,支撑轴力最终值变化不大,但基坑变形相对较大,这就说明预加力取小值的方法不利控制基坑变形。在城市复杂的周边环境和地质条件下,基坑变形是工程界关注的焦点,预加力取大值不仅有利于控制基坑变形,减小周边环境的风险,而且在下一层开挖前,利用较高的预加力检验支撑连接结点的可靠性[7],可增加支撑运营的安全性。
正确理解支撑轴力控制值的含义,合理确定轴力预警值。例如《江苏省城市轨道交通工程监测规程》(DGJ 32/J195—2015)[10]规定一级基坑的轴力控制值取支撑轴力设计值的60%~70%,并提出预警等级,预警值为控制值的80%。本文认为规范给定的控制值范围是工程设计与施工中应保证支撑轴力实测值的理想范围,相应地预警值范围也分0~60%和70%~100%的两个区间。低值区间的预警值可取支撑轴力设计值的48%,支撑轴力最小值为0,即支撑完全没有作用;高值区间的预警值为支撑轴力设计值的80%(即70%+10%),支撑轴力最大值为轴力设计值的100%,超出轴力设计值应由设计人复算。低值预警要求支撑轴力不能过小,避免钢支撑作用效果不明显,对基坑变形控制不利,同时还应避免出现因轴力不足钢支撑掉落事故发生。至于高值预警,本例的钢支撑轴力设计值最大为2 101 kN,小于《钢结构设计规范》(GB 50017—2017)[12]计算钢支撑承载力值Nmax为3 629 kN的80%,不存在钢支撑失稳风险。
合理的钢支撑预加力值的确定具有重要的工程意义。根据本文及文献[3-5,11]模拟计算结果,适当放大预加力值,可减小围护墙深层水平位移,同时结合钢支撑预加力施加过程中损失现象以及本文提出的高、低预警范围,建议预加力目标值为控制低值,即轴力设计值的60%,实际预加力值不低于48%,即不出现黄色低值预警;如果对于软土地基基坑工程,变形可能较大,预加力值目标值为控制高值,即轴力设计值的70%,实际预加值仍取不低于轴力设计值的48%。
5 结论
1)对于存在的钢支撑预加力不足现象,客观上是现有工程技术水平较低,主观上是工程技术人员未能正确理解轴力测项含义,将轴力测项与变形、水位等指标等同化,形成了支撑轴力越小就越安全的错误观念,忽视了预加力作为主动控制基坑变形的作用。
2)钢支撑预加力不仅是克服钢支撑理论抗压刚度小的有效方法,而且是验证钢支撑架设质量,提高钢支撑的实际抗压刚度的手段。
3)以钢支撑轴力设计值为参考,预加力比值与围护墙深层水平位移最大值具有负线性关系,但对轴力最终值的影响不显著;从施加的预加力效果看,预加力比值为40%时,经济性最佳。
4)针对支撑轴力监测项目的特殊性,提出了低、高双向预警和对应的预加力取值的方法。
