基于网络嵌入的稀疏子图发现算法

2020-10-18孙鹤立孙苗苗贾晓琳

计算机应用 2020年10期

孙鹤立，何亮，何方，孙苗苗，贾晓琳*

（1.西安交通大学计算机科学与技术学院，西安 710049；2.西安交通大学新闻与新媒体学院，西安 710049）

（*通信作者电子邮箱xlinjia@mail.xjtu.edu.cn）

0 引言

随着在线社交网络（如新浪微博、微信）的广泛流行，社团发现问题由于其广泛的应用得到了长足的发展。然而现有的多数工作大多关注于网络中的稠密子图发现问题，很少有关于稀疏子图（tenuous subgraph）的研究。所谓稀疏子图，是指由具有较少的连接或者弱连接的节点组成的子图结构。

稀疏子图在实际生活中有许多的应用场景。例如，在科研论文的审稿时，组织者需要为论文分派审稿人。除了需要审稿人的研究领域与论文内容相关之外，也需要避免审稿人与论文作者、审稿人之间互相认识，从而避免审稿时可能出现的学术不端现象，保证审稿过程的公平公正。当前多数审稿系统都使用了论文作者合作关系、工作单位、国籍等信息来避免研究领域的偏差，但是很少考虑到论文作者与审稿人之间的社交关系的稀疏性。弱社交网络中的好友推荐问题、患者治疗小组组建问题［1］同样与稀疏子图有关。可见，稀疏子图在现实生活中具有较为广泛的应用前景。

患者治疗小组组建：在精神康复治疗领域，针对某些疾病，如酗酒、药物依赖等，在对患者进行治疗时，通常是将有针对性的治疗和小组内患者之间的互助相结合的。这个治疗小组成员的选择不是随意的，而是需要满足一定的条件：尽可能保证治疗小组中的成员互不认识且没有共同的朋友，这样可以将治疗小组中共享的私人信息被传播的可能性降到最低，从而避免他们因为害怕熟识的朋友知道自己的秘密而不吐露自己内心的真实想法；且治疗小组的规模不宜过小，这样可以确保小组里的每个成员都能得到他人的充分的帮助。

评审专家选择：在审阅学术论文或项目立项评审时，均需指派专家。除了保证这些专家的研究方向与所评阅论文或项目的研究内容一致，还要尽可能避免审稿人和论文作者/项目申请人认识及审稿人之间互相认识，以确保评审过程的公平公正。

最近，稀疏子图开始引起了一些研究者的兴趣，研究者提出了一些用于稀疏子图发现的方法［2-4］，这些方法均基于图结构给出了稀疏子图的定义，并进行了相关研究。与之前的方法不同，本文提出一种基于网络嵌入的稀疏子图发现（Tenuous subGraph Finding，TGF）方法，将图结构转化为向量表示，进而在欧氏空间中进行稀疏子图的发现。通过这种方法能够更高效地进行稀疏子图的发现，并且可以很好地结合网络结构和属性信息。

1 相关研究

1.1 稀疏子图发现

稀疏子图相关的研究从2017 年才开始逐渐出现。Shen等［2］提出的MkTG（Minimumk-Triangle disconnected Group）问题是首个关于稀疏子图发现问题的研究。MkTG 问题使用子图中k-triangle 的个数来衡量子图的稀疏性。k-triangle 定义为子图中的一个三元组，其中任意两个节点之间的最短路径均小于k。MkTG 问题即为找到图中最大的一个节点集合，使得其中的k-triangle 的数量尽可能地少，并且节点数量尽可能地多。尽管该方法可以找到稀疏子图，但是k-triangle 在某些情况下不是一个很好的评估稀疏性的指标。另一方面，由于需要计算每个节点参与的k-triangle 的数量，导致该方法的时间复杂度较高，较难应用于大规模网络上的稀疏子图发现。在MkTG 问题的基础上，Li 等［4］提出KLM（K-Line-Minimized）用于稀疏子图发现。KLM 使用k-line衡量子图的稀疏性。k-line定义为图中最短路径小于k的一个节点对。KLM 问题尝试找到一个节点集合，使得其中k-line 的数量尽可能地少，同时节点的数量尽可能地多。

与前面两个工作不同，Hsu 等［3］提出了 UTNA（Unfamiliarity-aware-Therapy group selection with Noah’s Ark principle）问题，利用稀疏子图发现解决群体治疗问题。群体治疗是针对心理疾病进行治疗的主要临床手段之一，然而治疗小组的组建是相当有挑战性的。UTNA 旨在自动化地找出合理的治疗群体成员。UTNA 问题即找到一个最大的子图，使得其中连边的数目尽可能地少，且节点满足诺亚方舟准则（Noah’s Ark Principle）。

以上几种方法均是基于图结构寻找稀疏子图，并且均提出各自不同的关于稀疏子图的定义，然后基于这些定义设计了解决算法。然而，由于图结构的复杂性，这些关于稀疏子图的求解问题都是NP 难的，只能通过贪婪算法找到近似解，并且时间复杂度通常较高。随着网络嵌入方法在网络分析领域的流行，本文考虑使用基于网络嵌入的方法来寻找稀疏子图。

1.2 网络嵌入

网络嵌入（network embedding）［5-7］又称为网络表示学习（network representation learning），旨在将网络中的每个节点表示为低维向量，使原网络的拓扑结构信息被高效地保存于学习到的向量中。传统的网络一般用稀疏的邻接矩阵或拉普拉斯矩阵保存网络结构特征信息，在网络规模很大的情况下，这种表示会带来维灾难。网络嵌入将邻接矩阵映射成低维向量，很好地解决了维灾难问题。

近年来，随着深度学习的发展，越来越多的研究者开始采用深度学习中的技术解决网络嵌入问题。DeepWalk算法［8］对网络进行固定长度的随机游走，得到节点序列，然后使用Skip-Gram 模型对这些节点序列进行学习，从而得到节点向量表示。Node2Vec方法［9］基于DeepWalk 方法，对随机游走过程进行了改进，设计了一种有偏的随机游走方法，在深度优先搜索和广度优先搜索之间进行权衡。LINE（Large-scale Network Embedding）算法［10］则尝试在网络嵌入时保留网络中的一阶亲密性和二阶亲密性，通过最小化邻接矩阵和表示向量的KL（Kullback-Leibler）散度，可以在线性时间内高效地学习到节点向量表示。TADW（Text-Associated DeepWalk）算法［11］是一种针对文本属性网络的网络嵌入方法，在DeeWalk 的基础之上，加入了文本特征的学习，使用非负矩阵分解方法来进行优化。一些基于自编码器［12-14］的网络嵌入方法同样也能很好地学习到网络结构信息，如SDNE（Structural Deep Network Embedding）算法［12］、DNGR（Deep Neural Networks for Graph Representations）算法［13］等。

2 基于网络嵌入的稀疏子图发现算法

TGF 算法主要分为两个步骤：节点网络嵌入学习和稀疏子集发现。其中：节点网络嵌入负责对网络进行特征学习，在尽可能保持网络信息的情况下，将每个节点映射成低维空间中的表示向量；稀疏子集发现通过对学习到的节点表示向量进行学习，找到其中的稀疏子结构。

2.1 节点网络嵌入学习

本文主要基于Node2Vec 方法的思想进行网络嵌入。Node2vec是对DeepWalk 算法的改进，借鉴了自然语言处理中的词嵌入方法［15］。通过在网络中进行随机游走，得到节点序列，然后再使用skip-gram 方法即可学习到每个节点的表示向量。它的随机游走方法是深度优先遍历和广度优先遍历的一种权衡，通过设置参数控制游走在邻域停留或者往远处扩散。Node2vec 方法首先对网络中的邻域信息进行学习，然后对邻域信息保持目标函数进行优化完成节点表示向量的学习过程。这个目标函数是灵活的，而且有偏的随机游走方法使得该算法可以采样到不同类型的邻居结构。

Node2vec方法的优势在于它可以灵活控制随机游走的方式，很好地使原图中的结构信息得以保留。在原图中距离较远的两个节点，在低维向量表示空间中，它们的相对位置也会较远。Node2vec 综合考虑节点的DFS（Depth First Search）邻域和BFS（Bread First Search）邻域通过对深度优先遍历和广度优先遍历进行权衡，既能学习到局部的邻域结构信息，又能避免游走过远导致较远的两个节点形成相似的表示向量，充分考虑节点的“同质性”和“同构性”。“同质性”表示距离相近节点的嵌入向量应该尽量接近，“同构性”表示结构上相似的节点的嵌入向量应该尽量接近。

如图1所示，节点u和s1、s2、s3、s4之间联系非常紧密，它们组成了一个社区，应该具有相似的向量表示。同样地，节点v和s5、s6、s7、s8也应该具有相似的向量表示，它们也组成了一个社区。可以看出u和v分别是这两个社区的中心节点，它们在社区中扮演同样的角色，因此也应该具有相似的向量表示。Node2vec算法可以充分捕捉节点间的“同构性”。

图1 网络结构示意图Fig.1 Schematic diagram of network structure

2.2 稀疏子集发现

稀疏子集是由稀疏子图中的节点组成的集合，为了便于后续形式化描述，这里将稀疏子图问题转化为稀疏子集发现。在得到网络的节点表示向量之后，将稀疏子图发现问题从图结构中转移到了低维向量空间中。由于向量空间与图结构完全不同，原先在图结构上定义的k-line、k-triangle 等均无法使用，因此为了在向量空间中完成稀疏子集发现，需要重新定义向量空间中的稀疏子集发现问题。以下讨论中本文假设网络嵌入方法学习到的节点表示向量的维度为h。

首先需要考虑的是低维向量空间中稀疏性的度量方法。给定一个向量集合时，如何去评价它是否稀疏。本文可以通过计算样本之间的距离来判断两个点相距较近还是较远。对于一个向量集合，可以计算所有向量之间的距离，如果它们之间的距离都比较远，那么可以认为这个向量集合比较稀疏。为了衡量向量集合的稀疏性，本文引入ε对的定义：

定义1ε对，ε-pair。给定两个样本点的向量表示x1、x2，如果它们满足dis(x1，x2)＜ε，将其称为一个ε对。有了ε对的定义之后，就可以衡量给定的向量集合的稀疏性。假设集合T中的ε对的数量为r，r越小，说明集合T越稀疏。

这里的样本距离度量方式可以有多种，比如余弦距离、欧氏距离等。本文选用的距离度量为欧氏距离，即

下面给出向量空间中稀疏子集发现问题的定义：

定义2稀疏子集发现（tenuous subset finding）问题。给定欧氏空间Rh的散点集合，给定距离参数ε，从集合D中找到一个子集，使得T满足以下条件：

a）∀xi∈T，xj∈T，dis(xi，xj)＞ε；

b）¬∃xm∈{xi|xi∈D，xi∉T}。

其中：|T|表示集合中节点的个数；dis(xi，xj)为点xi与xj之间的距离。约束条件a）表明稀疏子集T中的任意两个节点间的距离需大于ε，即对的数量为0，这表明T中的所有节点间的距离都比较远，从而可以表明T比较稀疏；约束条件b）则表明稀疏子集中的样本数目应尽可能多。

为了解决定义2 中的稀疏子集发现问题，本文提出了一种基于局部密度扩张的贪婪算法TGF。TGF 算法的思路为：计算所有节点的邻居节点及邻居数目，首先选取邻居数目最少的节点u加到稀疏子集中，对于剩下的候选节点，在满足dis(u，xi)＞ε的条件下优先将邻居数目最少的节点加入到稀疏子集中。该算法在向稀疏子集中添加节点时总是选取当前状态下的最优节点，整体来讲是一种贪婪算法。

首先提出ε邻居的概念，定义如下：

定义3ε邻居（epsilon neighborhood）。对于点xi∈D，给定距离参数ε，则点xi的ε邻居Nε(xi)定义为：

Nε(xi)={xi∈D|dis(xi，xj)≤ε}

为了确保找到的稀疏子集中不存在ε对，在选取样本点加入到稀疏子集时，应该从候选集合中去掉该样本ε邻居中的所有样本点。为了避免过多的样本被删除，应尽量选择密度较小的样本点加入到稀疏子集中。在删除样本点时，其邻域内所有样本点的ε邻居都需要进行更新。

TGF算法的伪代码如算法1所示。

其中：第1）～2）行定义了相关变量；第3）～5）行是预处理阶段，负责计算出所有样本的ε邻居Nε(xi)以及ε邻居数量|Nε(xi)|；第6）～18）行是算法的主体部分，负责寻找稀疏子集并且删除不在稀疏子集中的样本点，其中第8）行将样本xt加入到稀疏子集中；第9）～14）行删除xt的ε邻居中的所有样本点，15）～18）行从候选集中删除样本点xt。

图2 为算法在二维空间上的稀疏子集发现过程。其中图2（a）表示初始化阶段，计算出每个样本的ε邻居和ε邻居数量，每个样本点旁边标示的数字即为样本的ε邻居的数量。图2（b）为TGF 算法最终找到的稀疏子集，所有的样本点的ε邻域数量都为0，可见所有的样本点的ε邻域内均没有其他样本点。

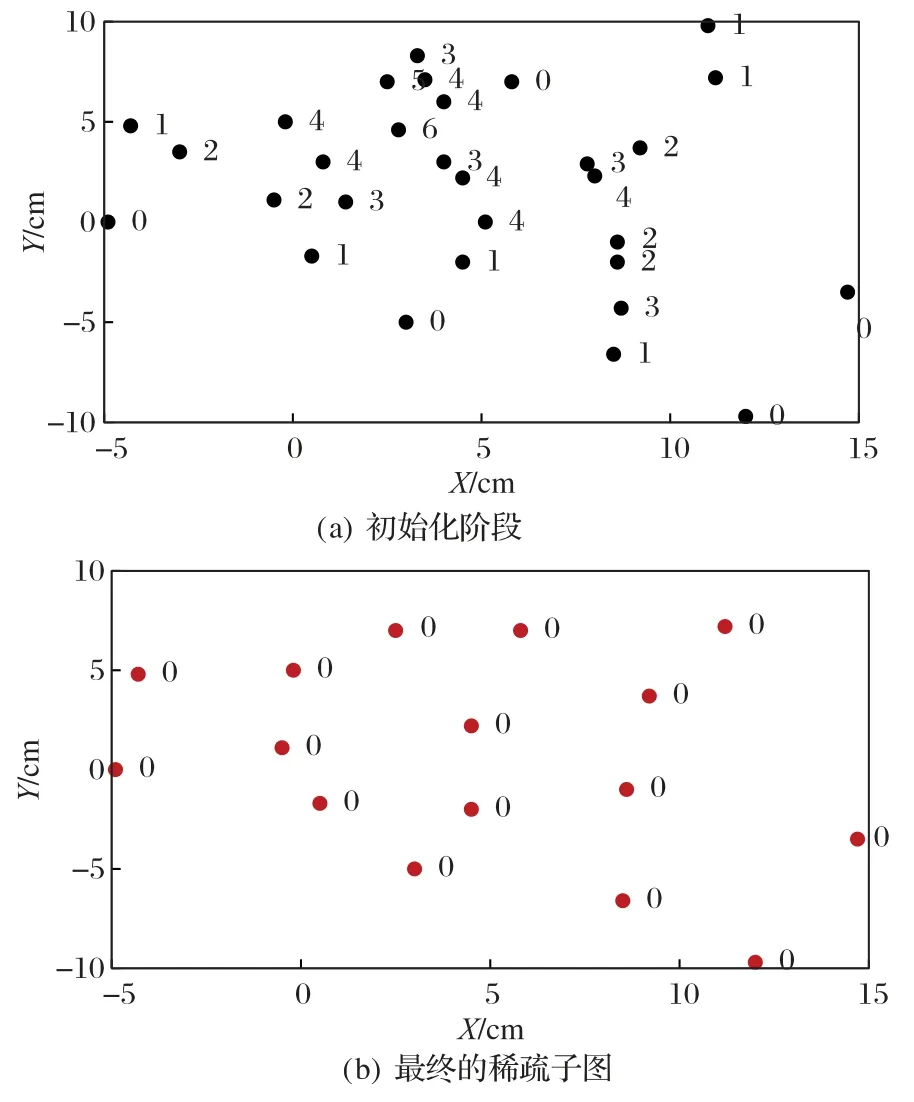
图2 稀疏子集发现过程Fig.2 Process of tenuous subset finding

2.3 时间复杂度分析

对于网络嵌入阶段，本文采用的是基于Node2vec 的网络嵌入方法，Node2vec 方法主要分为随机游走和skip-gram 的训练两个步骤。随机游走的时间复杂度为O(N)，skip-gram 的时间复杂度为O(logN)。对于ε邻居的计算过程，采用kd-tree数据索引结构，时间复杂度为O(NlogN)。对于稀疏子集发现的计算过程，每次添加样本点到稀疏子集中时，需要在未访问的样本中查找邻居数目最少的样本，采用线性查找的方法，时间复杂度为O(N)。删除给定样本的ε邻居中的样本这一步骤的时间复杂度为O(ρ2)，其中ρ表示平均每个样本的ε邻居个数。综上，稀疏子集发现过程总的时间复杂度为O(l(N+ρ2))，其中l表示集合D中的稀疏子集的个数，通常l≤N，可以近似认为寻找稀疏子集算法的时间复杂度接近线性时间复杂度，即O(N)。

综合以上分析，TGF 的算法时间复杂度为O(N+logN+NlogN+l(N+ρ2))，整理后即为O(NlogN+l(N+ρ2))。

3 实验与结果分析

为了评估TGF 算法的准确率和有效性，在多个人工合成网络和真实网络数据集上进行实验，并和已有的算法进行对比。本次实验的电脑环境为Interl Core i5-4590 CPU @3.2 GHz 型号CPU 和8 GB 内存，操作系统为Ubuntu 16.04，TGF算法采用Python语言实现。

3.1 实验数据集

本实验中采用的数据集分为人工合成网络数据集和真实网络数据集。数据集的所有相关信息总结在表1中。

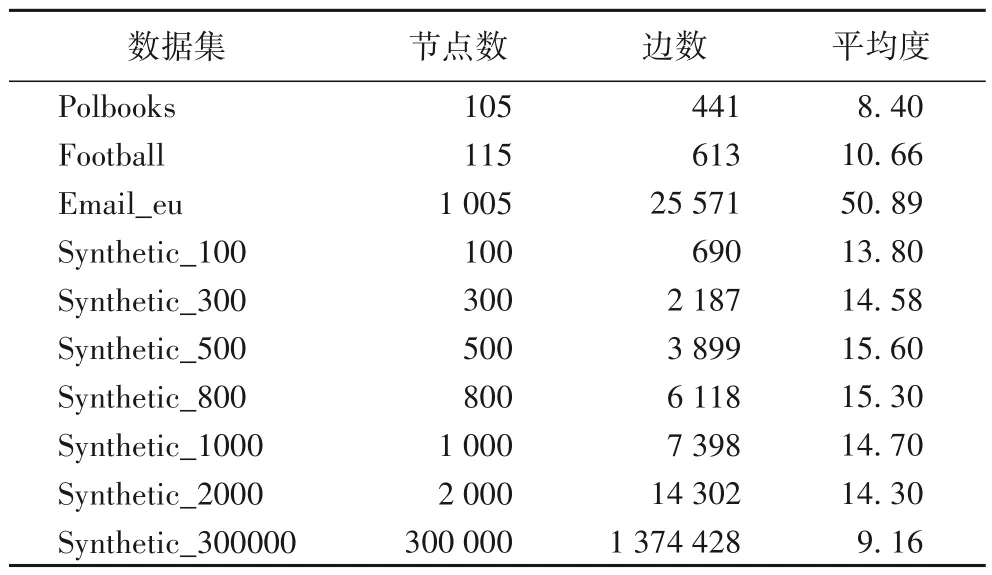
表1 数据集信息Tab.1 Dataset information

Polbooks 政治书籍网络：政治书籍网络是由亚马逊销售的政治书籍构成的网络，其中节点表示由亚马逊卖出的书籍，边则表示两本书经常被同时购买。每本书上都存在一个标签，表明该书籍的政治倾向性，分别为“自由”（liberal）、“中立”（neutral）和“保守”（conservative）。

Football 橄榄球联赛网络：Football 美国大学橄榄球联赛网络是由美国大学的橄榄球比赛情况构成的一个网络，其中的节点表示球队，边表示两个球队之间曾经打过比赛。该网络中一共有115 个节点和613 条边。网络中的所有球队被划分成了11个联盟和5支独立队伍。

Email_eu 研究机构邮件网络：Email_eu 是由欧洲某研究结构的邮件往来信息组成的网络。其中节点表示一个研究人员，边表示两个研究人员之间有过邮件往来。这些研究人员分属42个不同的科研机构。

表1 中的以Synthetic 开头的数据集表明它是一个人工合成数据集。人工合成数据集由Lancichinetti 等［16］开发的LFR benchmark 工具生成，在生成网络时可以指定网络的节点数目、平均度、混乱程度等。

3.2 对比算法和评估指标

为了评估TGF 算法的性能，本节选取两个已有的稀疏子图发现算法WK（Weight ofK-hop）和TERA（Triangle and Edge Reduction Algorithm）来进行对比。

在对实验结果进行衡量时，本文采了k-line、k-triangle 以及k-density 作为评价指标。关于k-triangle 和k-line 的定义详见1.1节。k-density的定义如下：

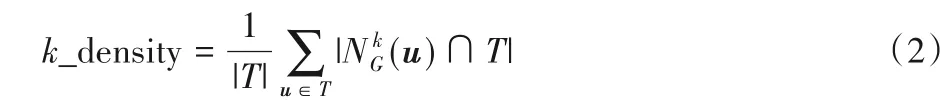
3.3 整体结果分析

本节主要分析各个算法在数据集上的整体表现。为了公平起见，设定在所有数据集上找到的稀疏子图规模是一致的，并且设定找到的稀疏子图的规模为原图规模的1/10。针对ε优化，使得TGF算法能找到指定大小的稀疏子图，且该稀疏子图中的1-line、1-triangle 以及1-density 值都较小。由于TGF 的时间复杂度非常低，所有要找到合适的ε并不困难。对于WK算法和TERA，为了找到指定规模大小的稀疏子图，需要多次尝试选择不同的k值。

表2 是WK、TERA、TGF 三个算法在人工合成数据集上的结果。其中：1-line 表示子图中边的数量；1-triangle 表示子图中直接相连的三个节点组成的三角形的数量；1-density 表示对应的子图密度；2-line 表示子图中最短路径长度不大于2 的节点对的数量；2-triangle 表示子图中三个节点组成的两两之间距离不大于2的三元组的数量；2-density表示对应的子图密度。从表2 中可以看到本文提出的TGF 算法在所有数据集上的1-line、1-triangle 和1-density 值都是最小的，找到的所有的稀疏子图中都不存在直接连边和三角形结构；然而TGF 算法在其他几个数据集上的2-line、2-triangle 和2-density 值较大，产生这种结果的原因可能是WK 和TERA 的直接目标就是最小化稀疏子图中的k-line数量和k-triangle的数量，而本文提出的TGF 算法并没有直接针对2-line 或2-triangle 进行优化。不过TGF 与这些方法得到的结果差距都非常小，也能在一定程度上表明TGF算法具有良好的性能。

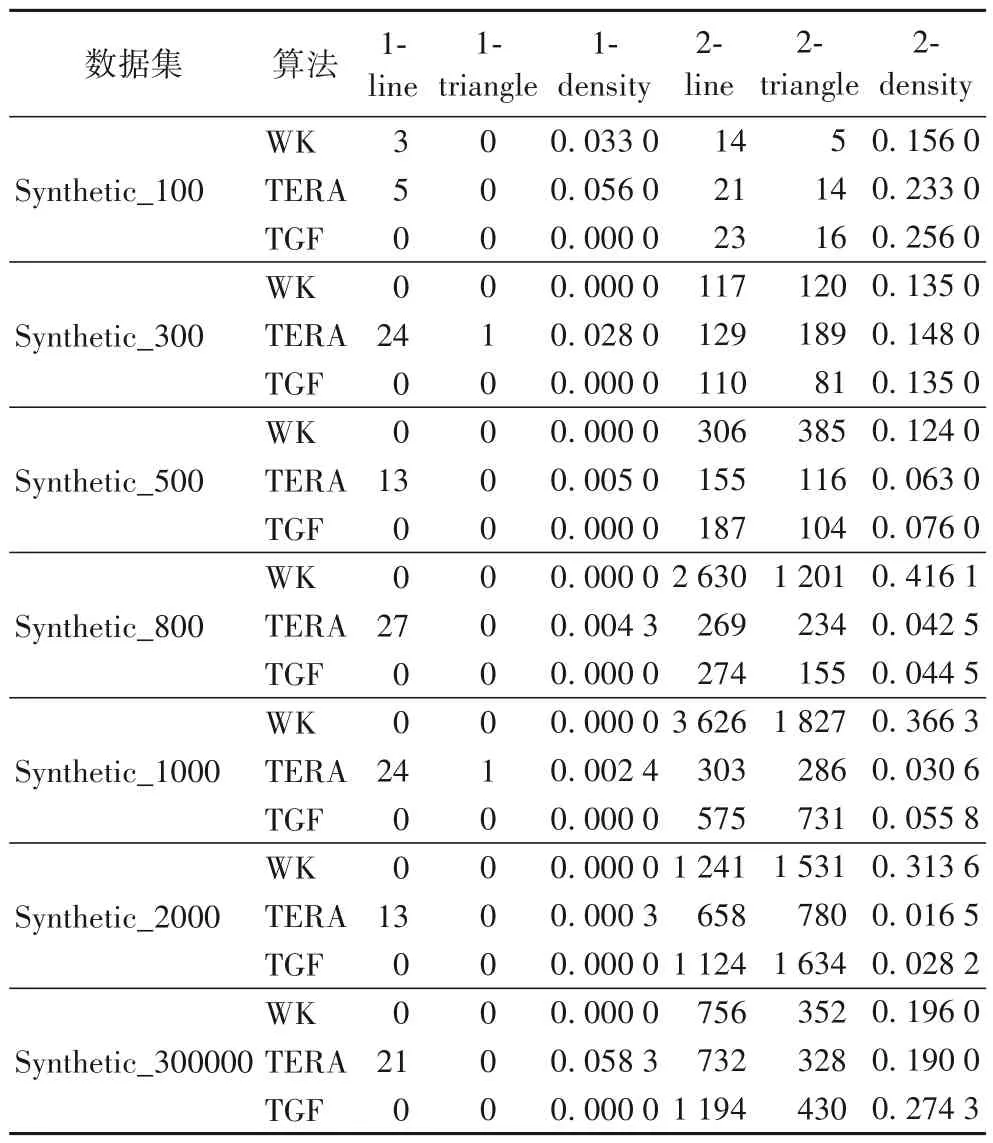
表2 各算法在人工合成数据集上的结果Tab.2 Results of different algorithms on synthetic datasets

表3展示的是三个算法在Polbooks、Football和Emai_eu三个真实数据集上的结果。从这两个表上可以看出TGF算法在这三个数据集上的1-line、1-triangle 和1-density 值都是最小的。TGF 在Polblooks 数据集上得到的2-triangle 值也是最小的。

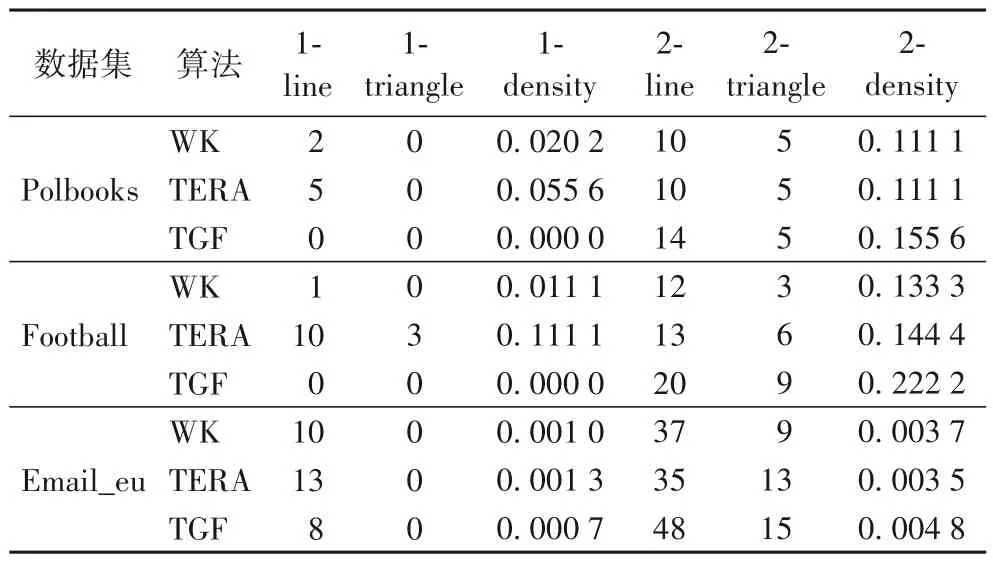
表3 各个算法在真实数据集上的结果Tab.3 Results of different algorithms on real datasets

综合以上分析，可以看出TGF 算法通过网络嵌入方法将网络结构映射到低维向量空间中，然后采用基于密度的稀疏子图发现方法来间接地完成稀疏子图发现的方法是可行的。该算法在所有的数据集上都展示出了优秀的性能，尤其在1-line、1-triangle 和1-density 三个指标上的值都小于WK 和TERA 两个对比算法。由于WK 和TERA 两个算法是直接对2-line、2-trangle和2-density这三个指标做优化的，所以这两个算法在这三个指标上的值相对较小，但是TGF 算法在这些指标上的值与WK 和TERA 的差距非常小，说明TGF 算法具有良好的性能。

3.4 参数敏感性分析

本文提出的TGF引入参数ε来度量向量之间的距离，ε对结果有较大的影响。为了分析TGF 算法的参数ε对性能的影响，本文在两个人工合成数据集上进行了实验，分析随着参数ε从小到大的变化，对应找到的稀疏子图中各项指标的变化情况。图3 展示了TGF 算法在Synthetic_800 和Synthetic_2000、Synthetic_300000 三个数据集上的参数敏感性分析情况。

图3 TGF算法在三个数据集上的参数敏感性情况Fig.3 Parameter sensitivity of TGF algorithm on three datasets

图3 中：纵坐标表示算法得到的1-line、1-triangle 个数和找到的稀疏子图节点数，即n_tenuous。从图3中可以看出，随着参数距离ε的增大，得到的1-line，1-triangle 个数均开始逐渐减小，并且呈现出快速下降的趋势。这说明TGF 对参数ε较为敏感，如果ε过小，TGF 可能返回整个数据集作为稀疏子图结果集。而随着ε的增大，由于TGF会删除选定点的ε邻域内的所有节点，所以n_tenuous 的个数开始快速降低。从Synthetic_800 数据集上得到的结果可以看出：1）当ε＜2.2 时，TGF 会返回整个数据集作为稀疏子图结果集；2）当ε在2.5～3.0 时，得到的1-line、1-triangle 和n_tenuous 个数开始快速下降；3）当ε=3.0时，是一个拐点，在ε＞3.0以后，得到的1-line、1-triangle 和n_tenuous 个数下降速度开始减慢；4）当ε＞4.0时，1-line、1-triangle 和n_tenuous 个数都变成了0。在Synthetic_2000 和Synthetic_300000 数据集上呈现出了类似的结果，当ε在2.5～3.0 时，算法得到的1-line，1-triangle 和n_tenuous 个数呈现出快速下降趋势；在ε＞4.5 之后，1-line、1-triangle和n_tenuous个数都归为0。

综上可知，ε参数对得到的稀疏子图的影响较大，选择合适的ε能得到较好的结果（稀疏子图规模较大且子图较稀疏），而如果ε选得过小或者过大则有可能导致返回整个数据集作为稀疏子图结果集或者稀疏子图结果集为空。在多个实验数据集上的结果表明，ε选择在区间1.5～4.5 时，TGF 算法能取得较好的效果。

3.5 实例分析

为了更好地展现出TGF 算法寻找稀疏子图的效果，本节选取Polbooks 数据集进行实例分析，展示TGF 算法在该数据集上的稀疏子图发现结果。

图4 是TGF 算法在Polbooks 网络上找到的稀疏子图的示意图。其中较大的节点表示通过TGF 算法找到的10 个节点，它们共同组成了一个稀疏子图，可以看到这个稀疏子图中的节点均匀地分布在整个网络中。在该稀疏子图结构中，任意两个节点之间都不存在连边。由此可见，TGF 算法在真实网络上的效果很好，能够有效地找到网络中的稀疏子图结构，并且有足够的稀疏性。当然，由于这里的ε参数取值为0.8，此时只找到了10 个节点。如果将ε参数取得更小，那么TGF 能找到规模更大的稀疏子图；反之，将ε参数取得更大，那么找到的稀疏子图规模就会更小。参数ε的选择可以根据实际需要找到的稀疏子图规模来决定。

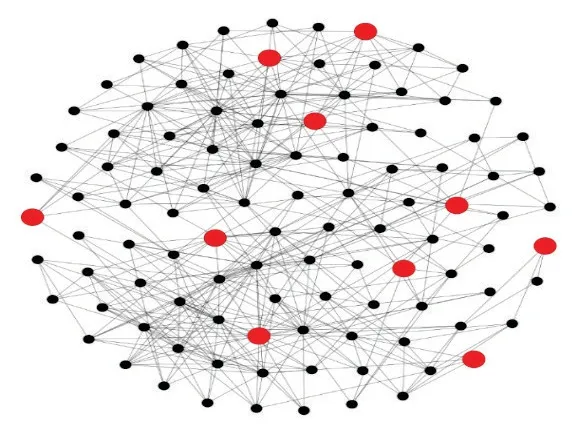
图4 Polbooks网络上找到的稀疏子图Fig.4 Tenuous subgraph found in Polbooks network

3.6 时间性能分析

本节主要比较TGF算法和其他对比算法的时间效率和可扩展性。表4 为WK、TERA 和TGF 算法在多个人工合成网络数据集上的运行时间对比。这里分别采用了三个人工合成数据集。为了公平的进行比较，本文在对比WK、TERA 和TGF三个算法的运行时间时，设定在所有数据集上找到的稀疏子图规模是一致的。

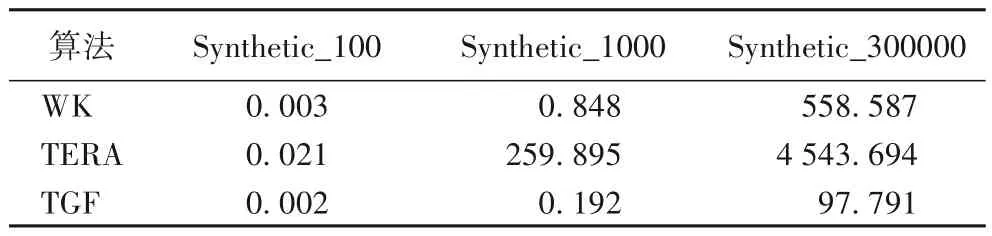
表4 各个算法在不同数据集上的运行时间单位：sTab.4 Running time of different algorithms on different datasets unit：s

从表4 可以看出，相较于其他两个算法，TGF 算法的时间效率是最高的，且随着网络规模的增大，TGF的优势变得更为明显。TGF算法的运行时间较低的原因有两个方面：一方面，TGF 通过网络嵌入方法将图结构映射到低维向量空间中，在向量空间中的距离计算相对于图中的最短路径计算复杂度大降低；另一方面，TGF 采用了哈希表存储所有节点的ε邻居信息，因此查询和删除样本的速度很快，得到稀疏子图的时间几乎是线性的。

4 结语

本文提出了基于网络嵌入的稀疏子图发现方法，将网络结构映射到低维空间中。在Synthetic_100、Synthetic_1000、Synthetic_300000 三个人工生成数据集上的时间性能分析表明，TGF 算法展示出较好的效果，在Synthetic_1000 数据集上与TERA 和WK 算法相比，TGF 算法的搜索效率是TERA 的1 353 倍，是WK 算法的4 倍。同时通过在真实数据集和人工生成数据集上的实验结果表明，本文方法在1-line、1-triangle、1-density 指标上的结果也较优。本文没有考虑属性图上的稀疏子图发现问题，网络中节点的属性信息也是非常重要的，比如性别属性、年龄属性、背景属性等信息，后续会结合节点属性展开相关研究。