让天下没有难学的数学

华应龙

有很多人认为，数学之所以难学，既有数学学科的特点，也有学生的原因，更有老师的原因。但笔者认为，身为教师更应从自身找原因。教师们面对经过多位专家编写、多轮审查的国家教材，就更应该有信心把课本上的“一切知识有趣、有效地教给一切人”。这是教师的责任和使命。

一、数学是否真的难学

很多人都说数学难学，它到底难在哪？真的难学吗？笔者认为，要回答这一问题教师是关键。作为一名数学老师要“手下留情”，有时教师不经意的一句话、一个举动也许会斩断学生的奇思妙想。当教师让学生觉得数学难学了，那数学就不是数学了。这样，教师就会“了断学生的一门心思”。其实，数学并不难学。

接下来，笔者和大家分享三个案例，看看数学是否真的难学。这三个案例分别是数与代数领域的“找次品”、图形与几何领域的“角的度量”、统计与概率领域的“游戏公平”。

1.找次品

通过实践教学，这节课的确有一定的难度。那么，它到底难在哪？这节课最重要的目标是什么？为了达成目标，教师必须“舍”去什么？经过阅读、思考、推敲，笔者通过以下方式来组织这节课。

笔者首先出示一组玩跷跷板的图片，然后问学生：“什么时候把你翘到天上去？”学生就此开始畅所欲言。接着，笔者和学生们聊比尔·盖茨，当学生说“比尔·盖茨开了一家公司叫微软”后，笔者追问：“为什么叫微软？”因为比尔·盖茨特别喜欢一个中国人叫老子，老子说“上善若水”。最高的善像水一样，所以硬不好、软不好，微软才好。

微软公司招聘员工时，出过这样一道题：“假定你有81个乒乓球，其中只有1个球比其他球稍重。如果只能利用没有砝码的天平，请问你最少要称几次才能保证找到稍重的球？”如果是你去应聘，你将如何作答？学生大概的回答是：80、1、40。笔者让学生说说理由，他们说出了各自的道理。学生们围绕三个错误答案进行交流，让他们更好地理解了题意。此时，笔者特意帮学生概括：天平可能平衡，也可能不平衡；重球有可能在左边、右边或下边，这三种情况都有。

对这个问题的研究看似有点难，但其实不难。老子说：“天下难事，必作于易。”笔者问学生：“你觉得这个问题从几个球开始思考比较合适？”笔者引导学生从最简单的2个球开始研究，只需称一次就能找到。那3个球最少需要称几次才能找到？有学生说3次，笔者请他进一步说明。后来他说着说着，发现不对了，原来只需1次。很多的时候，学生错着错着就对了。

笔者指着2个球和3个球的板书说：“同学们，能提出什么问题吗？”有学生说：“怎么球的个数多了，最少还是一次呀？”经过讨论，学生们明白了：原来3个球中，只称了2个，第3个球是推断出来的。那么，4个球呢？通过对不同的称法进行比较，学生们明白：既然要保证找到，就要从最坏的角度去考虑，最少需要称2次。有了4个球做铺垫，那8个球呢？学生会很自然地得到3次。若是9个球呢？学生通过分析得知：4、4、1，答案是3次。此时，笔者便问：“还有不同的想法吗？”有学生提出3、3、3，称2次就能保证找到。笔者再请学生确认：最少2次，怎么保证？然后，我指着8个球和9个球的板书说：“同学们，能提出什么问题吗？”一石激起千层浪：“9个球2次，8个球怎么3次了？” “球的个数多了，怎么称的次数还少了？”随之学生便发现问题了：8个球，2次就能保证找到。比较不同之后，学生们发现：分成3份比分成2份好。于是，笔者提出了这样一个问题：“天平几个盘子？”当有学生狐疑地说“3个”时，笔者接过话头说：看到天平有三个盘子，高明；用上第三个盘子，就是高手。

再回到81个球，学生基本都能将其分成“27、27、27”，最少4次就能找到重球。最后揭题“找次品”，即找几个有意思的次数，慢慢来品一品。当学生们品出方法、品出道理时，难题就变简单了。

此时，笔者再请学生们诵读完老子的“道生一，一生二，二生三，三生万物”后，便说：“同学们，世上的事物往往都是一分为三的：上、中、下，左、中、右，好、中、差，正数、负数……”学生齐答：“零。”笔者说：“质数、合数”学生齐答：“1”笔者说：“过去、现在”学生齐答：“未来。”……大家都开心地笑了。

2.角的度量

这节课是刘坚教授2005年布置给笔者的任务，上课地点在河南郑州。

拿到课题时，笔者就思考：①我们让学生量了各种各样的角，学生感受到了量角的用处了吗？量角的大小是屠龙之技，还是生活中必不可少的技能？②“角的度量”一课教学的难点是什么？为什么会有这样的难点？量角器的结构很复杂，量角之前先要认识量角器，那要认识量角器的什么呢？原来只是认识中心点、0刻度线、内圈外圈刻度，就认识这些吗？还有吗？怎么认识量角器？关于量角的技能，以往教学中简要概括出了“二合一看” “0度刻度线在左边看外圈，0度刻度线在右边看内圈”等。教师一步一步地教，可到量角时，学生拿着量角器，转来转去，都不知道把量角器怎么放到角上，遑论读出度数了。为什么学生还是不会量角？③教师的教学有三个层次：教知识、教方法、教思想。以前我们只是教了量角的知识和技能，那这节课可教给学生什么方法？让其思想有所提升呢？

笔者回忆以前的教学：没教之前，学生怎么量？您看过学生这么量的吗？（见1图），为什么这么量？这使学生知道量角是要用角对着角来量。问题只是在于学生不知道量角器上的角在哪，如果能帮学生认识到量角器上的角在哪里，那量角就水到渠成了。原来，我们之前的教学犯了“只见树木不见森林”的错，对“点、线”等局部都有了认知，但对组合起来的整个“角”没有认识。

接着，就可以简单的分享一下这节课：先后出示三个滑梯（见图2），教师问学生：“玩过吗？想玩哪个？现在呢？”学生们笑了，笑后是醒悟：第三个滑梯不能玩，第一个滑梯不好玩。再问：“这三个滑梯的不同之处在哪里？”学生们不约而同地说：“角度不同。”

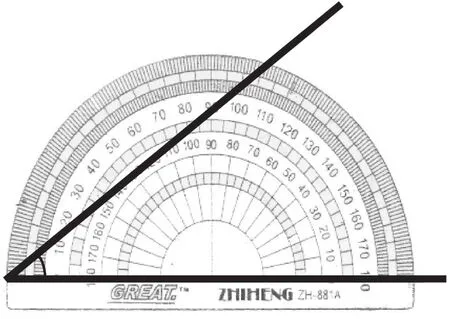
图1 角的度量

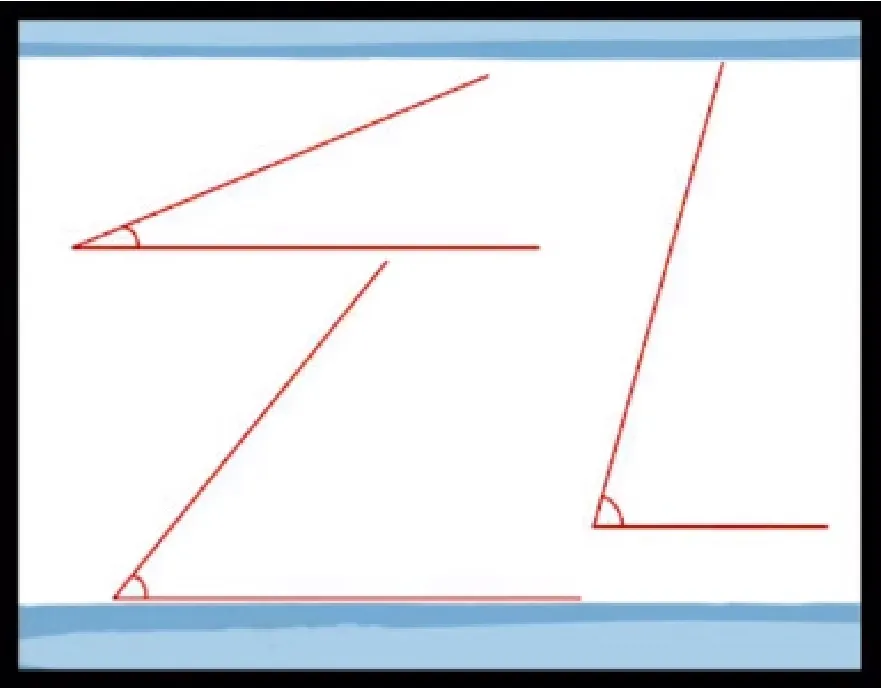
图2 观察三个滑梯的不同之处

教师接着问学生：“滑梯的角多大才合适呢？这时就需要量角了。怎么量角？”学生们兴奋地说：“用量角器。” 教师：“会量吗？” 学生信心满满：“会！”“那就自己量吧！”每次量的时候，都有学生像图1那样量。 于是，笔者便请学生上台展示，此时就有学生质疑。笔者先肯定展示的学生勇于尝试，再肯定他对准了零度刻度线，然后肯定他知道量角就是用角对着角，最后还要感谢他带给大家的思考和启发。

现在的问题是量角器上有角吗？它的角在哪？我让学生在量角器上画90°的角、60°的角、1°的角和156°的角，分别是直角、锐角、单位角、钝角。学生们在量角器上看到了若干个大小不同的角，接着笔者便呈现了开口朝向不同的角，这是教材中没有的，学生们量得不亦乐乎。

“儿童散学归来早，忙趁东风放纸鸢。”笔者组织学生思考：怎么放风筝才是比他人放得高？只要量出风筝线和地面所呈的角度即可。笔者再呈现学生们熟悉的椅子，餐桌边配的椅子其后背向后倾斜9°，学习的椅子其后背向后倾斜8°，沙发的靠背一般向后倾斜11°。然后，回到开始的问题：滑梯的角多大才合适呢？笔者告诉学生们：“我请教了三位工程师，滑梯的角在40°到56°之间。”最后，笔者带着学生回忆测量长度、面积、角度的方法，还用了华罗庚的一句话“数起源于数，量起源于量”作为总结。

这样去教“角的度量”，才能让学习像呼吸一样自然。

3.游戏公平

下面是2008年在上海，刘坚教授安排笔者在全国教学研讨会上上的一节课。这节课的关键是要不要做实验？有时不做实验学生很清晰，做了实验，学生反而糊涂了。鉴于此，笔者就思考：这节课做什么实验呢？到底怎么做实验？

关于这节课，大家一定会回想到尴尬的场面：课上让学生抛10次硬币，学生抛出了2次正面、8次反面；或9次正面、1次反面。这样的事件经常发生。小概率事件怎么变成大概率事件了？这是为什么？鉴于此，教师请大家思考：一个硬币抛1米高和1厘米高，可以同日而语吗？原来我们只规定了实验的次数，没有规定实验的高度、力度和角度。

结合刚刚闭幕的北京奥运会，笔者上出了一节被张奠宙先生高度称赞的课。只有一张奥运会篮球决赛的门票，笔者和儿子谁去现场看呢？儿子提议抛啤酒瓶盖来决定：正面朝上，儿子去；反面朝上，爸爸去。笔者问学生们：“这个方法好不好？”然后，组织学生把啤酒瓶盖装在水杯里抛10次，最大限度地上下甩三次，再记录。这就是规定实验的方法。

学生的汇报是：5∶5；6∶4；2∶8。试了之后，问题就来了，还有三种不同的答案，怎么办？有的学生建议多做几次，有的学生建议把组内的结果综合起来。六大组合计的结果，都是反面朝上比正面朝上多很多。接着，笔者让学生观察与思考：为什么反面朝上的可能性大？

学生们的说法各异，笔者笑而不语。其实，笔者笑的目的就是让学生思考，到底哪个对？老子说：“不自是，故彰。”笔者受益于李烈校长的指导，课堂上要教师画龙，学生点睛。当学生捅破窗户纸的那一刻，笔者便不说话，给学生一个原型启发就够了。课件上出示踢毽子的图片，踢的毽子为什么总是立着？学生通过观察与思考之后，马上明白了：为什么抛啤酒瓶盖不公平？因为啤酒瓶盖两面不均匀，一面重一面轻。那抛什么公平呢？抛硬币，为什么？因为硬币两面均匀。老子说：“反者道之动。”不均匀的，才需要用频率来表达概率。抛完不均匀的，结论不公平。反过来呢？均匀的，自然就公平。

在实际教学中，总是有学生问笔者：“老师，最后篮球谁去看的啊？”他们还在故事里呢！于是，笔者接着讲故事，告诉学生们：“我儿子已经上大学了，他的数学学得特别好，高考150分的数学，他考了147分。是复查时，他把对的，改错了，否则，满分150分。我想他一定知道啤酒瓶盖正面朝上的可能性小，但他自己选择了正面，有这样的儿子真好！成人之美，成全别人就是一种美。我遵从儿子定的规则，请夫人来抛。我夫人一抛，结果居然是正面朝上。”学生们惊叫起来：“啊，怎么会啊？”然后，我让学生猜测分析。有学生说：“您夫人喜欢您儿子。” 有学生说：“您夫人想让您儿子去看。” 有学生若有所思地说：“您夫人把反面加重了。”还有的学生说：“正面朝上的可能性小，但也是有可能的。” 我笑而不语。当学生们都说了后，笔者问：“想知道为什么吗？请看屏幕——”

课的最后，回到奥运会上来。笔者说：“抛啤酒瓶盖，不公平，因为啤酒瓶盖两面不均匀；抛硬币，才公平，所以奥运会上很多比赛都是用硬币来决定的。”学生们惊讶了：“奥运会怎么可能抛硬币决定？”录像呈现奥运会中乒乓球、羽毛球、足球、网球等比赛中，抛硬币来选择场地的片段。学生们信服了，满足了。

二、数学应如何教才不难学

分享完这三节课，大家是否觉得数学真的难学？那么，怎么教数学就不难学了呢？

1.从教学内容上来说，先深入、再浅出

这三节课都是先深入，然后再浅出的。

深入，就是明晰这一教学内容的本质。在设计“角的度量”一课时，笔者追问出了量角的本质，即量角就是用量角器上的角对着要量的角。在思考“找次品”一课时，笔者意识到要从“一分为二”发展到“一分为三”，天平实际上是有三个盘子的。“游戏公平”的背后是硬币问题，是一种古典概率，是不需要做实验的；只有不均匀的，才需要做实验，去找频率来近似地表达概率。

浅出，就是要从学生的生活，从玩耍和游戏展开，就是在讲一个故事。“角的度量”是滑滑梯引入的；“找次品”是跷跷板引入的，讲的是比尔·盖茨的故事和老子的故事；“游戏公平”讲的是观看奥运会的故事。

认识数学的本质，先深入、再浅出，数学就不难了。

一位特级教师说：“数学的本质在于自由，而我们的老师却常常按照现有规范的知识或规定去约束儿童思考，并以此为标准去评判对错。所以，儿童的心思就被套牢在迎合成人们的期待上。”“实际上，解决一个问题有很多途径，只要逻辑上没问题，在形式上就没有对错之分的，但很多教师却不这样认为。即使错，有时候也有错得有道理之说……教师们哪来这样的视野和胸襟啊？”

另一位特级教师说：“数学难在光记住结果是无法灵活运用的，所以从学习方法上而言，不能仅采取记忆的方法。需要从已有知识经验出发，经历知识生长的过程。”

由上面两位特级教师的看法，笔者认为：深入，还有一层意思，即需要深入认识数学教学的本质——思维的体操，要借着数学知识，来教会学生去如何数学地思维。

通过笔者近40年的小学数学教学经历，发现了一个规律：数学学得不好的学生，都喜欢“死记硬背”，不会动脑筋，因此“积懒成笨”。只去记忆，不去思考，是学不好数学的。

针对思维的体操，怎么浅出呢？那就是“想错了，更好玩。”

2.从教学过程来看，想错了，更好玩

笔者的教育理念是“化错教育”。“化错”是指把课堂教学中的差错融化为一种教学资源，相机融入后续的教学过程中，化腐朽为神奇，变“事故”为“故事”。这与我国古代“相生相克、相反相成”等哲学思想相契合。

化错的要义是在教学过程中随机融入，自然生成，而不是事先刻意安排；敏锐发现差错背后的意义，揭示其内在的矛盾、张力，巧妙地彰显其积极意义，而不是简单地否定学生的错误；充分挖掘并利用差错资源的多方面价值，培养学生直面错误、超越错误的求真人格，让其学做真人，将教学活动引向深入，引向心灵深处，而不仅仅是促进学生认知的发展。

对学生有价值的差错，笔者会引导学生鼓起三四次感谢的掌声。首先，为勇于尝试，不盲从的坚持；其次，为其有根有据的说理；再次，为其接纳他人观点后的修正；最后，为其带给大家思考的贡献。

从这三节课例中，大家可以看到，错误是学生自然生成的，有差错，才有真正的学习，才有实质性的学习活动发生。有化错，才有教师期待已久的主动学习、独立思考和创新活动发生。让学生们在错误中多飞一会儿，错着错着就对了，这会使学生感受到“化错就像是在做思想的魔术”，使他们不再怕错，进而开启他们的思维。所以，有化错的课堂，才有学生快乐健康地成长。

3.从学生的角度来讲，喜欢了，就不难

笔者一直在教数学，也一直在做教学管理工作，从中笔者深感：不喜欢孩子的人，请不要做老师；不喜欢数学的老师，请不要教数学；如果任何人都能教的，那一定不是数学。古人说：亲其师信其道。学生喜欢某一学科的老师，那门学科就一定能学好，而且会乐此不疲。作为数学教师，笔者奉行如下“三段论”。

周国平先生说：“我不想知道你有什么，只想知道你在寻找什么，你就是你所寻找的东西。”笔者在寻找数学，所以笔者就是数学。因此，笔者的第一本书取名《我就是数学》。“我就是数学”的含义是：你若问我喜欢什么？其回答是：“我就是数学。” 你若问我能干什么？其回答是：“我就是数学。” 你若问我在学校里是什么？其回答是：“我就是数学。” 其实，教师就是他所教学科的形象大使。你若问我一个人一辈子、一件事，我做的一件事是什么？其回答是：“我就是数学。”“我就是数学”乃是自我安顿、自我鞭策，也是自我期许，既用数学修身，也用数学育人，还用数学立命。

数学不只是公式、符号、规律，还有故事、想象、画面和无限的可能，一样地拥有诗和远方。和学生一起玩数学，让学生打开思维的翅膀，遨游于数学的海洋，感受到“数学好玩”了，学习自然就不会感到困难。