一种基于径向速度残差曲线拟合的车载SINS零速修正算法

韩勇强，王新健，孙寿才，陈家斌

（1.北京理工大学，北京 100081；2.北京航天发射技术研究所，北京 100076）

基于纯惯性解算的导航方法是地面移动平台的一种重要工作模式，其不受地面条件、电磁干扰等外部因素的影响，具有高度的自主性与可靠性，但导航误差随时间累积的问题较为显著。零速修正是提高陆用平台惯性导航系统定位定向精度的一种廉价且有效的方法[1]。传统的零速修正方法包括二次曲线拟合以及卡尔曼滤波方法等[2-5]，这些方法需要每间隔一段时间进行停车修正，且行进过程中的定位精度发散趋势较为明显。在卡尔曼滤波方法基础上，文献[6-8]从不同角度提出了一种基于运动学约束的车载捷联惯性导航误差阻尼算法。该算法利用车体运动信息构建观测方程，实现了车体运动状态的不完整约束。但由于实际车体运行时，运动约束条件难以严格保证，可能导致卡尔曼滤波发散，且由于非完整约束导致纵向速度无法准确估计，在某些特定形式状态（如长时间同向行驶）时误差阻尼效果不佳。因此本文在动态零速修正算法（DZUPT，Dynamic Zero velocity update）的基础上提出了一种结合径向误差曲线拟合的自适应动态零速修正算法（CA-DZUPT，Curve-fitting and Aaptive Dynamic Zero velocity update），提高车载捷联惯导长时间行驶定位精度。经车载实验证明，在每间隔15分钟停车一次的条件下，定位精度可以达到10 m（CEP）。

1 DZUPT 算法

1.1 动态约束条件

理想情况下，当车体处于运动状态时，只要不发生跳跃和侧滑，车体坐标系内其天向与侧向的速度为0。

其中m为车体坐标系，x，y分别指向车体右侧及正前方，z轴垂直于x，y轴并形成右手坐标系。

1.2 算法模型

选取姿态误差、速度误差、位置误差、陀螺漂移、加速度计零偏及惯导安装误差角误差（俯仰与航向误差角）为17 维观测量设计卡尔曼滤波器。

假设陀螺漂移及加速度计零偏均为常值，则有以下系统误差方程[9]:

式中，

式(4)中Mxx为捷联惯导系统状态方程中的对应项，其含义为

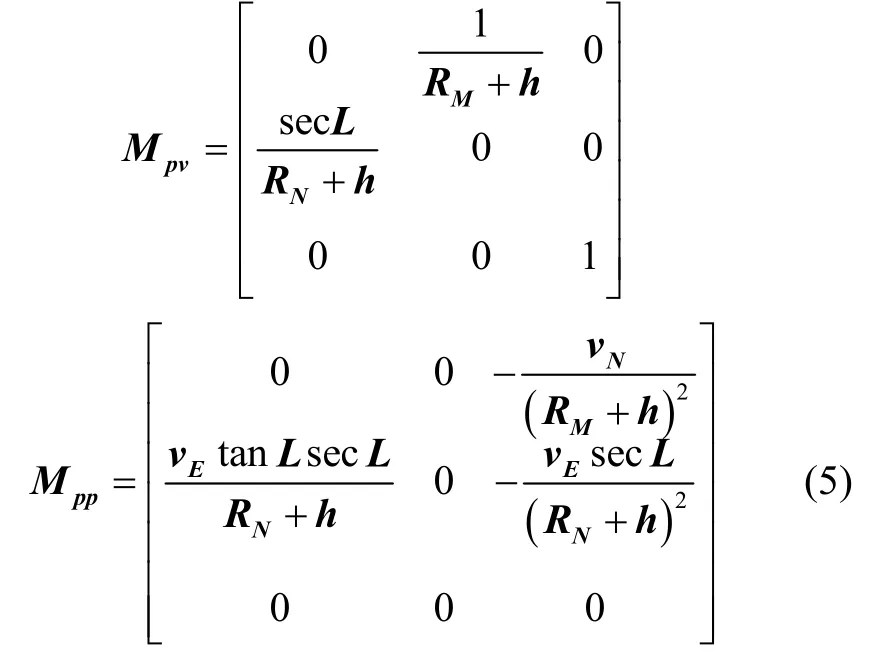
其中，RM和RN分别为子午圈及卯酉圈曲率半径，ωie为地速，L为当地纬度，vE、vN为东西向速度。

惯导系统输出的导航系（取东北天坐标系）速度为Vn，姿态转换矩阵为，由于惯导安装误差角的存在，车体坐标系的速度分量可按式(6)计算:

其中，n表示东北天地理坐标系，b表示捷联惯导体坐标系，m表示车体坐标系。

可利用车体坐标系x轴速度和z轴速度为零的约束条件构成量测值:

考虑到惯导安装误差角的剩余误差为小量，可以得到

结合式(8)，对式(6)进行全微分可得

动态条件下滤波器的量测方程为

其中V为等效量测噪声，H为量测矩阵，其定义为

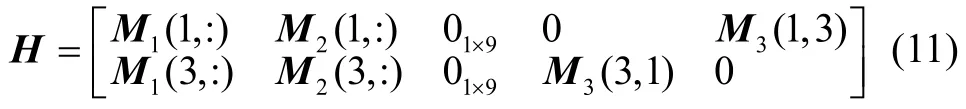
式中M1(1,:)表示矩阵M1的第一行，其它类似形式含义相似。

在车体实际行驶过程中，由于惯导不可能与车体运动中心完全重合，除了惯导与车体之间存在安装误差角，还存在外杆臂效应。平稳行驶外杆臂影响较小，可忽略不计，转弯幅度较大时，可以考虑不进行量测更新或将外杆臂扩充为状态变量，此处不再赘述。

2 CA-DZUPT 算法原理

由动态零速修正的约束条件可知，卡尔曼滤波只对车体的侧向以及天向速度误差进行观测，当载体处于长直路线行驶时，径向速度误差会产生显著积累而无法消除，导致定位精度变差。由此想到，可以在DZUPT 基础上利用自适应噪声以及曲线拟合的方法将定位误差拟合出来，在车体停止时将其补偿回输出值。

2.1 零速检测

准确地获取零速区间是进行零速修正的关键。本文采用角速度检测（ARED）方法，通过获取陀螺仪的数据对车体的零速进行判定[10]。若车体处于零速区间，需满足:

误判率和可探测率通常是评估零速探测器性能优劣的两项指标，其含义做如下定义:

可探测率P(S)及误判率P(F)两项指标可以用来评判零速区间探测器的性能。可探测率P(S)及误判率P(F)可按照式(13)计算得出:

其中，len（*）代表所用实验数据集中数据的长度，D为实际的零速区间数据,D1为检测到的正确的零速区间数据，D2为被误判为零速区间数据的非零速数据，D′为由零速检测器检测到的零速区间数据。

经过不同窗口长度实验测试，该方法可行且检测准确。本文系统某次实验的零速检测结果如表1所示。

表1 不同窗口长度的影响Tab.1 Effects of different lengths of window

2.2 Sage-Husa 自适应卡尔曼滤波

动态零速修正过程采用Sage-Husa 自适应卡尔曼滤波方法，它是一种次优无偏后验噪声估计算法，能够利用量测过程中采集到的数据，对系统的系统噪声和量测噪声进行实时的估计[11]。而动态零速修正过程中，约束条件不完整，惯导系统模型存在误差，量测噪声难以选择，不合适的参数易导致滤波发散。

系统噪声主要由系统本身结构决定，受环境影响较小；而量测噪声受外界环境影响较大。为解决卡尔曼滤波零速修正算法在行驶、停车等不同状态条件下的滤波器参数问题，本文采用Sage-Husa 自适应卡尔曼滤波方法对量测噪声进行实时自适应估计。

首先确定自适应估计的加权系数

其中b为遗忘因子，本文中设为0.9。由式（14）可知，随着时间推移，dt逐渐接近1-b。

量测噪声的实时估计为

其中ϵt为残差，Pt+1∣t为一步预测均方误差矩阵。Rt在更新过程中始终保持正定。

2.3 径向速度误差曲线拟合

在实验过程中我们发现，基于自适应卡尔曼滤波的动态零速修正算法在长时间沿直线行驶过程中，其误差修正效果相对于有航向变化的线路有明显的下降，而在停车时的静态零速修正作用也不显著。通过理论分析，其主要原因在于动态零速约束算法的不完整性，缺乏载体行驶方向速度误差的有效阻尼，从而导致径向导航误差的累积。而在停车时，虽然能够准确观测到径向速度误差，但由于滤波器模型并未考虑径向残差，导致难以实现累积位置误差的准确估计。

本文提出了一种基于径向速度误差曲线拟合的零速修正方法，利用停车修正环节，可以实现对动态零速修正过程中由径向速度残差所导致定位误差的有效补偿。

曲线拟合法是指将速度误差变化过程拟合成一条曲线，再将此曲线进行积分得到动态零速修正后的位置误差校正值。由于采取纯惯性工作模式，车体行驶过程中没有精确的外部速度参考，无法获取速度误差，因此利用零速检测器检测到停车时，用此时的速度输出值作为速度误差进行计算。假设停车时刻为T，此时的径向速度误差残差为ΔV，位置误差ΔP可表示为

由于动态零速修正过程对惯导侧向以及天向速度已经进行了补偿，导航系内的速度已经不再满足舒拉震荡特点，此时必须针对惯导坐标系纵向速度误差导致的位置误差进行建模拟合。图1为某次实验的长直路段一个停车周期（15 min）内惯导系纵向速度误差的变化情况。

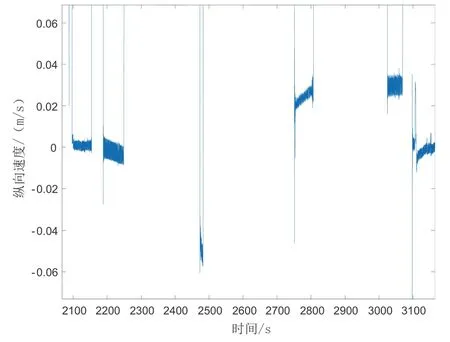
图1 一个停车周期内惯导径向速度变化Fig.1 Radial velocity change of SINS during one stop cycle

由图1可以看出，纵向速度误差走势可以用高次曲线进行近似拟合。由于停车间隔较长，所以将模型进行了简化。以n次曲线为例，假设0 时刻经过零速补偿的速度误差为0，那么τ时刻的速度误差δ vb(τ)可表示为

其中幂次常数n=1,2 …N，则参数，其中ΔV为停车时刻观测的径向速度误差，T为本次停车与上次零速修正的时间间隔，则式(16)可以转化为

其中Δτ为惯导解算更新周期。由于停车时刻ΔV与T为已知量，只需在车体处于运动状态时持续计算，待到停车时刻得到ΔV，进行修正计算出ΔP即可。

在实际测试时发现，由于停车间隔内径向速度误差的累积特性比较复杂，二次曲线并不能很好地拟合出径向速度误差的变化，其估计出的位置误差绝对值偏大，需要采取其它曲线模型进行拟合。仿照上述推算过程，使用3 次、4 次等高次曲线进行拟合，最终发现当n=4 时位置误差补偿效果最佳，并使用多组实验对其效果进行了验证。

3 实验验证

3.1 实验设备组成

实验所用设备如图2所示。

实验主要设备由高精度激光陀螺捷联惯导系统、与高精度实时差分GPS 组成。惯导采用高精度激光陀螺双轴转位捷联惯性导航系统，系统参数如表2所示。

图2 实验设备Fig.2 Devices for experiments

表2 陀螺仪和加速度计基本参数Tab.2 Basic parameters of gyroscope and accelerometer

GPS 实时记录车体经纬度坐标，作为标准参考位置，其定位误差为0.01 m。与CA-DZUPT 定位结果进行对比，计算惯导定位精度。

3.2 实验路线

实验路线全程35 km，共行驶约90 分钟，实验路线图如图3所示。

图3 实验路线Fig.3 The route of experiments

图中圆形标注点为停车点，相邻停车点时间间隔约为15～17 分钟，路程约为6.5 km。

3.3 实验结果

本文实验共进行五组，实验前首先将激光系统进行约5 min 的初始对准，然后沿图3所示路线行驶，并将各组实验定位误差进行记录。图4为不进行零速修正，天向速度约束条件下惯导定位误差图。

图5为仅使用DZUPT 方法时，第一组实验的定位误差。由定位误差曲线可以看到，当仅采用DZUPT算法时，虽然动态定位误差得到了较好的抑制，但由于采用了速度、位置实时反馈的补偿策略，状态量δvnδp,滤波器增益K保持在较小范围，从而在停车时，虽然能够观测到较明显的速度误差，但对位置误差的补偿幅度很小。

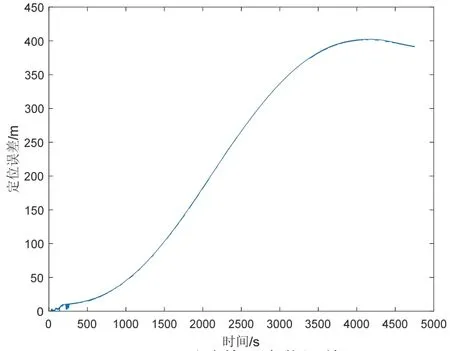
图4 无零速修正定位误差Fig.4 Positioning error without zero velocity update

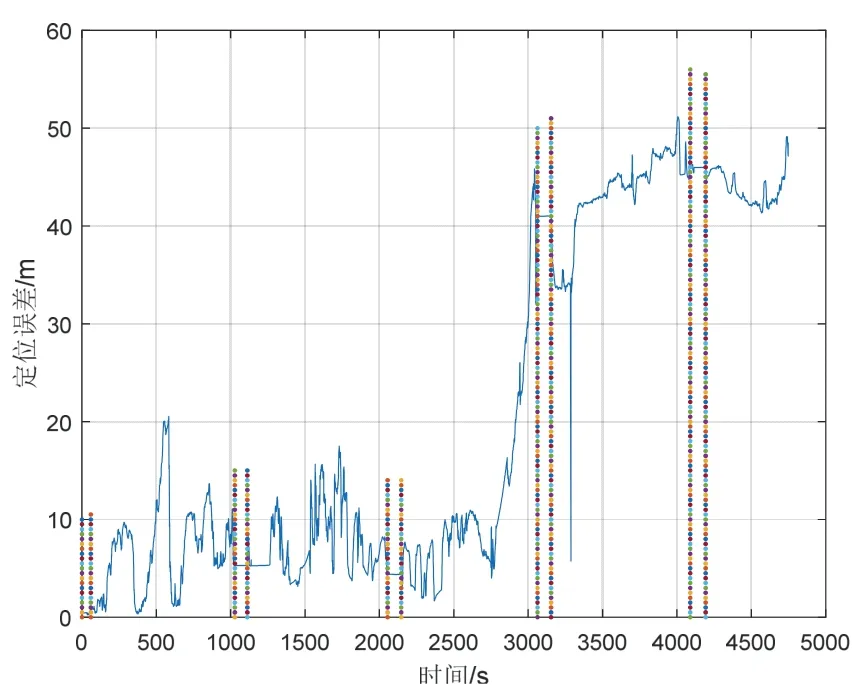
图5 DZUPT 实验定位误差Fig.5 Experiment positioning error of DZUPT

图6～7 为使用CA-DZUPT 算法修正，第一组实验的定位误差，虚线标注区间为图3中停车点。

图6 CA-DZUPT 实验定位误差Fig.6 Positioning error of CA-DZUPT experiment

图3中表明，第二个停车点到第三个停车点（对应2000 s～3000 s 的时间区间）之间为东西方向的一条长直路线。由图7中的实验结果可知，在该时间段，东向误差快速增长，而北向定位误差保持在很小范围。最后一个停车点处情况类似，只是北向误差增长较快，东向误差较平稳。该现象同时也体现出动态零速修正算法对侧向导航误差的抑制效果较好，而对径向误差的累积较难补偿。

图7 CA-DZUPT 实验东向、北向定位误差Fig.7 East and north positioning errors of CA-DZUPT experiment

按照上述实验方法，共进行了5 组对比实验，结果见表3。

表3 15 分钟停车间隔两种算法对比实验定位误差（DZ：DZUPT，CA：CA-DZUPT，单位：m）Tab.3 Positioning error of comparison experiments of two algorithms under a 15-minute stop interval（DZ：DZUPT，CA：CA-DZUPT，Unit:m）

从实验结果可以看出，使用DZUPT算法修正后，动态条件下的定位精度有显著提高，但停车对导航误差修正效果没有显著提升。而使用CA-DZUPT 算法后，定位精度大幅提高，达到15 min 零速间隔10 m（CEP）。

4 总 结

本文提出了一种基于自适应卡尔曼滤波与径向速度残差结合曲线拟合的车载激光陀螺捷联惯导自适应动态复合零速修正算法。在DZUPT 算法的基础上，引入Sage-Husa 自适应卡尔曼滤波，解决了量测噪声自适应调整的问题，提高了动态修正时滤波算法的鲁棒性；由实验数据出发，分析了动态零速修正过程中的径向速度残差问题，提出了基于高次曲线拟合的径向速度残差补偿算法。经多组车载实验验证，本文提出的CA-DZUPT 算法稳定有效，系统15 min 零速修正间隔条件下定位精度达到了10 m（CEP），算法具有重要的理论意义与工程价值。