格网坐标系下自适应反馈增益阻尼方法

奔粤阳，张瀚轩，崔文婷，尹冬寒

（1.哈尔滨工程大学自动化学院，哈尔滨 150001；2.中国船舶工业集团公司第七〇八研究所，上海 201100）

由于极区处于高纬度地区，受其特殊地理位置的影响，经线在极点附近收敛于极点，这使得常用的指北方位机械编排和游移方位机械编排都不再适用[1]。针对该问题，有学者提出横坐标系惯导系统[2-4]和格网坐标系惯导系统[5-7]两种导航方式并得到一定的发展。通过分析发现，基于横坐标系和格网坐标系的两种机械编排仍然存在舒勒周期、傅科周期和地球周期三种振荡，这对于长时间航行的舰船来说，需要采用一些技术去消除这些周期振荡来提高惯导系统的导航精度[8-10]。文献[11]和文献[12]分别基于横坐标系惯导系统和格网坐标系惯导系统推导了系统的误差模型并采用了传统阻尼网络算法，有效地抑制周期振荡到来的误差。但是这种传统阻尼网络通常存在两个问题:阻尼网络参数的选择需要进行不断的试凑；参数一旦确定就无法改变，这与我们希望在导航初期系统具有较大阻尼比使得误差快速收敛，进入稳态后系统具有较小阻尼比减小载体机动的影响相矛盾。

本文针对传统阻尼网络设计存在的问题，设计了一种自适应反馈增益阻尼方法。该方法在无阻尼格网惯导系统中加入自适应反馈增益，该反馈增益可以通过有效估计手段进行求取并且能够根据外速度信息的变化进行实时地调整，从而抑制格网惯导系统的振荡误差。仿真结果表明，本文所设计的自适应反馈增益阻尼网络能够加快惯导系统误差的收敛速度，减小系统阻尼状态切换时产生的超调量。

1 格网坐标系建立及导航原理

1.1 格网坐标系的建立

如图1所示，以载体所在地P点处平行于格林威治子午面的平面作为格网平面，以载体所在地的水平面作为切平面，格网平面与切平面的交线定义为格网北向，格网北向同真北方向的夹角记为σ，格网天向同当地地理天向重合，格网东向在切平面内且与格网北向垂直构成右手直角坐标系，此即为格网坐标系G系（eGE,eGN,eGU）。可见，G 系同样为P点处的水平坐标系，仅与当地地理坐标系g 系（东-北-天）在方位上偏差σ角。其中，L、λ分别为载体所在地的纬度和经度，ωie为地球自转角速度，eE,eN,eU分别为当地地理坐标系的东向、北向和天向。

图1 格网坐标系Fig.1 Grid coordinate system

1.2 格网坐标系导航原理

以格网坐标系为导航坐标系，它的运动学方程与采用固定指北方位类似，由于格网北向同真北方向存在夹角σ，所以两者的主要区别是一些运动参数在导航系下的投影分量不同。根据文献[13,14]，假设地球为圆球体，可以得到在格网坐标系下惯导系统的运动学方程:

姿态基本方程:

速度基本方程:

位置基本方程:

式中

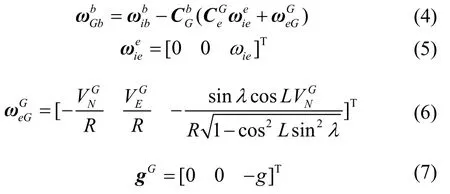
2 自适应反馈增益阻尼方法

通过对格网坐标系下惯导系统的运动学方程进行分析,并假设系统中陀螺仪和加速度计的安装误差和标度因数误差已经得到补偿，可以建立惯导系统的误差模型，即无阻尼误差模型。在无阻尼误差模型基础上，通过加入反馈的方式，将原本临界稳定的系统转换为渐近稳定的系统[15]。我们假设在地球是圆球体的情况下，加入反馈增益的格网惯导系统误差方程为:

位置误差方程:

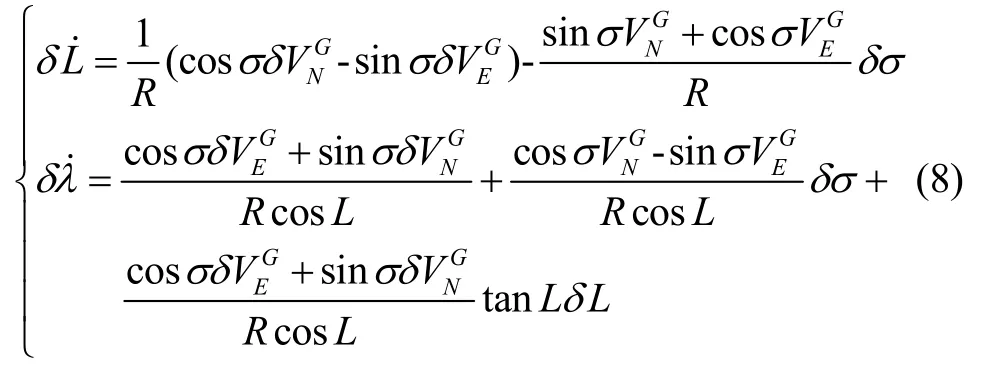
速度误差方程:

失准角方程:

格网角误差方程:

其中，R为地球半径，g为重力加速度，δL,δλ分别为纬度误差和经度误差，分别为格网坐标系下的东向和北向速度误差，分别为格网坐标系的东向、北向和天向失准角，δσ为格网角误差，分别为格网坐标系下的东向和北向加速度计误差，分别为在格网坐标系下的东向、北向和天向陀螺漂移。Ux1,Ux2,Uy1,Uy2分别为北向和东向回路的反馈控制量，它们的具体表达式为:

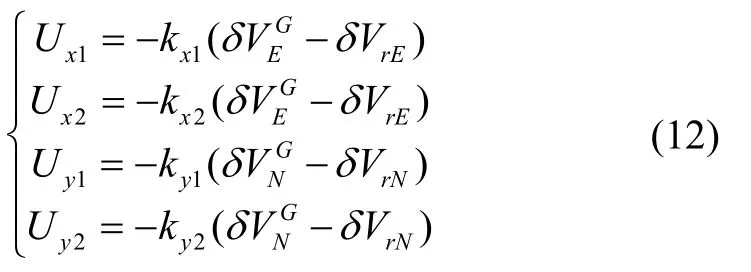
其中kx1,kx2,ky1,ky2为自适应反馈增益，分别为格网坐标系下外速度参考误差。为了更加容易地研究探讨问题，假定是在静基座情况下，此时舰船不运动，即。根据加入反馈增益的格网惯导系统误差方程画出加入反馈增益格网惯导系统方框图，如图2所示。

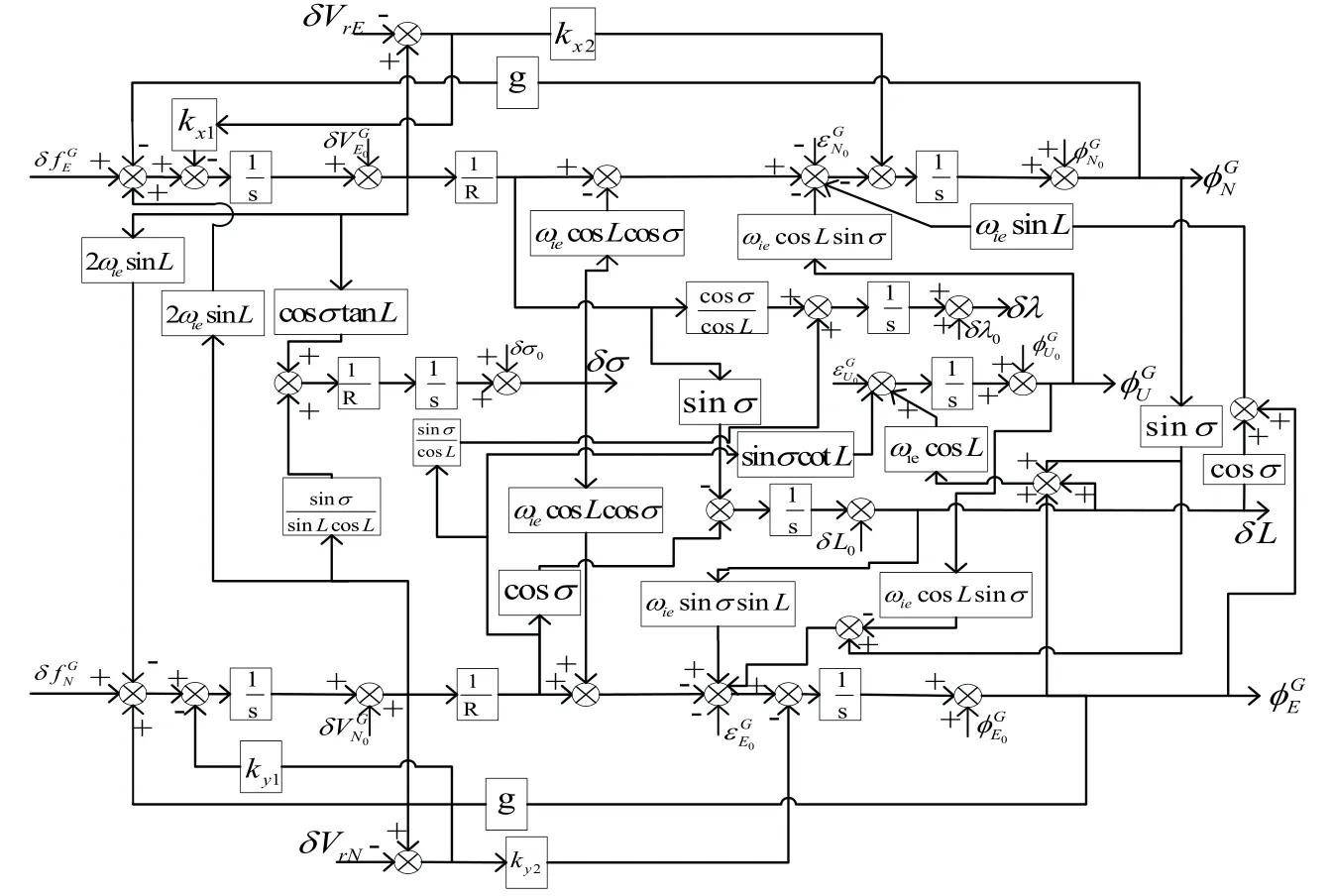
图2 加入反馈增益格网惯导系统误差方框图Fig.2 Add feedback gain grid inertial navigation system error block diagram

由图2可见，纬度误差δL和格网角误差δσ包含在系统的闭环回路中，当整个系统稳定的时候，纬度误差和格网角误差亦将是有界的，即不会随时间的增长而产生积累误差；但对于经度误差δλ却不然，它是开环的，即经度误差会随着时间积累而产生积累误差。

下面具体分析在两个水平回路上加入反馈增益后，是如何使周期振荡误差得到抑制的。因为傅科周期振荡调节舒勒周期振荡，所以我们忽略傅科周期振荡的影响。我们不难得到忽略傅科振荡周期后，加入反馈增益惯导系统误差方框图的特征多项式为:

对比无阻尼格网惯导系统的特征多项式:

可见，当kx1,ky1＞ 0;kx2,ky2＜0时，在两条水平回路上加入的反馈增益会使舒勒周期振荡误差分量得到抑制，但地球周期振荡误差仍然存在。当然傅科周期振荡误差分量也将随着舒勒周期振荡的抑制而消失，这将说明前面所述的忽略傅科周期振荡是可以被允许的。如果我们选取两水平通道的反馈增益相同，即k1=kx1=ky1,k2=kx2=ky2的话，式(13)可以化简为:

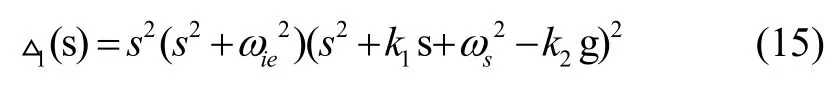
此时格网惯导系统东向和北向水平回路的特征多项式均为:

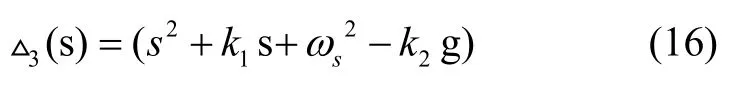
将按式(16)设计的水平阻尼系统等效为典型二阶系统，根据系数对应原则可得到在水平回路上引入反馈增益后惯导系统的阻尼比和自然振荡角频率为:

其中，ξ为系统阻尼比，ωn为自然振荡角频率。

也就是我们可以通过动态调节k1,k2的取值来调节水平回路中阻尼比的大小。在导航初期较大的阻尼比可以使系统的振荡误差快速收敛，进而使舒勒周期和傅科周期振荡误差得到抑制，从而起到了阻尼的效果；系统达到稳态后，较小的阻尼比会减小载体机动对系统造成的不利影响。

如何动态地调节k1,k2取值就成为了本文的研究重点。受Kalman 滤波原理[16]的启发，可以将原本的控制问题转化为估计问题[17]，通过求解滤波中的增益矩阵K得到加入到惯导系统中水平回路的反馈增益k1和k2的值。

从图2中可以看出，格网惯导系统北向水平回路误差模型和东向水平回路误差模型是彼此对称的，所以我们仅以北向水平回路进行分析。

首先将加入反馈增益格网惯导系统北向水平回路模型写成矩阵的形式，表示如下:

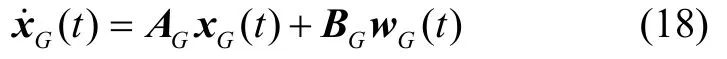
其中

通过式(18)可以看出，惯导系统误差状态变量北向速度误差和东向失准角仅受k1和k2的影响。那么我们想使两个误差状态变量达到最小，就需要得到最优的反馈增益k1和k2。下面给出求解反馈增益k1和k2的方法。

首先设计一个随机的线性系统M 系统，M 系统的系统模型如下所示:

其中，A1、B1、C1分别是M 系统的系统矩阵、输入矩阵和输出矩阵，x1、y1分别是系统的状态向量和观测向量。其中，y1为惯性系统速度与外速度之差。

然后对M 系统使用龙伯格观测器进行估计，可以得到系统状态变量的估计方程为:

如果我们令

则惯导系统误差状态变量xG(t)和M 系统的状态变量(t)变化规律就会相同；此时我们可以得到:

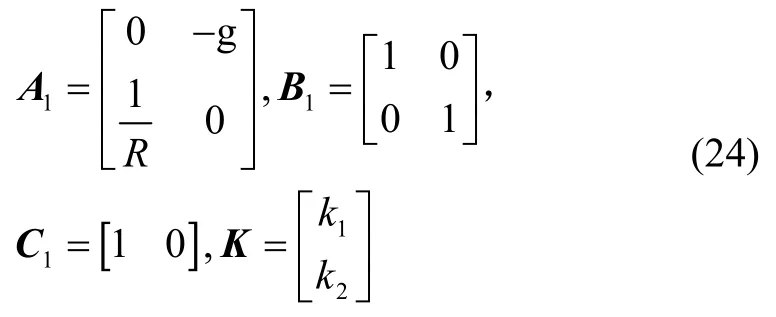
那么M 系统就由随机线性系统变成了一个确定的线性系统，并且(t)和xG(t)的变化规律相同，问题也就从寻找使xG(t)达到最小的k1和k2变成了寻找使(t)达到最小的增益矩阵K。我们又知道Kalman滤波的原理就是去求解增益矩阵K使得估计误差的协方差达到最小，那么我们就可以对M 系统利用Kalman 滤波技术，求解出增益矩阵K的值。通过式(24)，我们就进而得到了k1和k2的值。此时求得的反馈增益k1和k2会使北向速度误差和东向失准角的协方差达到最小。另外我们考虑到引入外速度的同时，同样引入了外速度误差，我们应该实时根据外部速度信息的质量来进行调整，外速度信息有效时可以使系统处于外速度水平阻尼状态，而外速度信息无效时，即我们的量测噪声Rk∉［Rmin,Rmax］，可以自动切换至无阻尼状态，因此本文采用简化的自适应滤波方法，具体实施过程如下所示[18-19]:

计算加权系数:

一步预测均方误差:

计算新息序列:

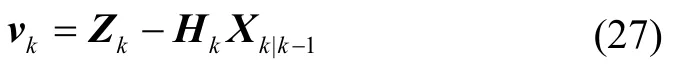
估计量测噪声:

计算滤波增益:

估计均方误差:

状态一步预测:

状态估计计算:

其中，φk,k-1、Γk-1、Hk是已知的系统结构参数，分别称为状态一步转移矩阵、系统噪声分配矩阵和量测矩阵。给定初值P0,R0,Q0,b,k=1，以及量测噪声的界限Rmax,Rmin；置位:k=k+ 1；b为遗忘因子，常取b=0.9 ～0.999。在自适应滤波过程中，量测噪声Rk与系统的状态和状态估计协方差交错在线估计，采用遗忘因子可以限制滤波的记忆长度，加重新近观测数据对现实估计的作用，每次更新完量测噪声Rk与量测噪声界限进行比较，若不在规定的范围内，则视为外速度信息无效，自动将反馈增益赋零使其转换为无阻尼状态。

以上即为通过自适应滤波方法求取格网系统北向回路反馈增益矩阵K的全过程。将矩阵K中的k1和k2带入到自适应反馈增益北向水平回路中，可以使东向失准角和北向速度误差有效抑制，达到阻尼的效果。同时也可以利用式(17)求得新阻尼网络中的阻尼比，该阻尼比是随k1和k2变化而变化的，因此进一步验证了本方法在格网系统中加入了变阻尼的思想。

同时我们还需要考虑我们加入的自适应反馈增益是否可以使格网北向回路稳定。基于线性系统理论，若系统是可控又可观测的，那么该系统就是稳定的[20]。所以我们需要进一步验证系统的可观测性和可控性。

由式(24)所示的系统，其可观测性矩阵为

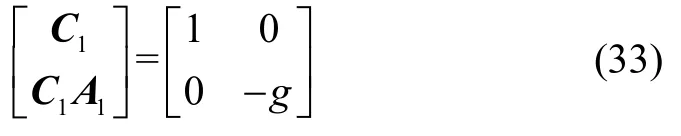
由式(33)可知，该系统的可观测性矩阵为满秩，即系统完全可观。

由式(24)所示的系统，其可控性矩阵为

由式(34)可知，该系统的可控性矩阵为满秩，即系统完全可控。这就表明由自适应kalman 滤波求解得到的反馈增益k1和k2可使格网北向水平回路达到稳定状态。

3 仿真实验

为了验证所设计的格网坐标系下自适应反馈增益阻尼方法有效性，对该方法进行了36 小时的仿真验证，并与无阻尼方法和传统外速度水平阻尼方法进行了对比。仿真的初始参数设置如表1所示，载体沿着120 °经线以10 m/s 的速度向北匀速航行。计程仪参考速度误差设置如下:t＜10h或t＞30h时，计程仪提供的外速度随机误差波动较大，无法提供准确的外速度信息；10h≤t≤ 30h 时，计程仪提供的外速度误差较小，可以提供准确的外速度信息。为了更好地验证自适应阻尼算法，本文设置了计程仪阶段性常值误差变化，当10h≤t≤ 20h 时，计程仪提供的外速度误差为-0.5 m/s；当20h≤t≤ 30h 时，计程仪提供的外速度误差为0.5 m/s。仿真中的初始参数如表1所示。

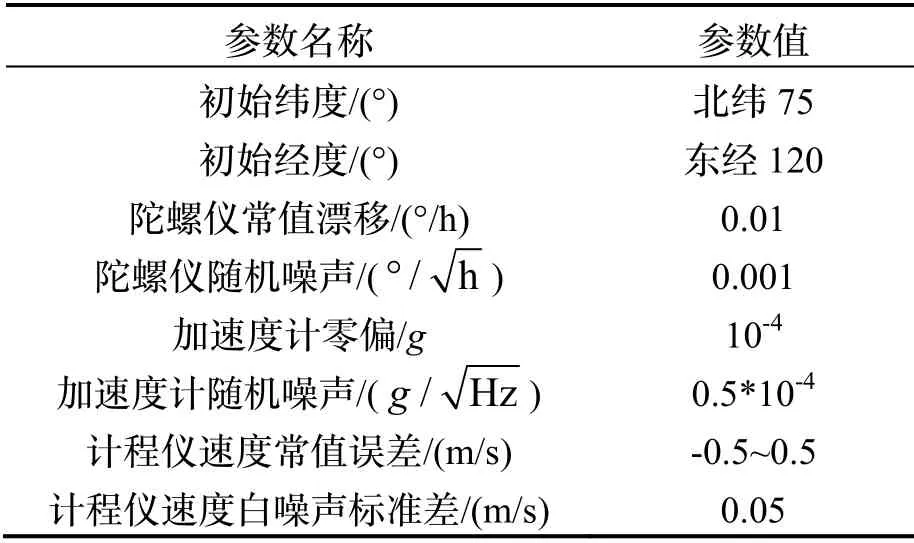
表1 初始参数Tab.1 Initial parameters

无阻尼方法、传统外速度阻尼方法和本文设计的自适应反馈增益阻尼方法的误差结果对比如图3～5所示。图中蓝线为无阻尼情况下的误差曲线，红线为采用传统外速度水平阻尼方法的误差曲线，黑线为采用本文方法的误差曲线。

图3 速度误差对比图Fig.3 Velocity error comparison diagram

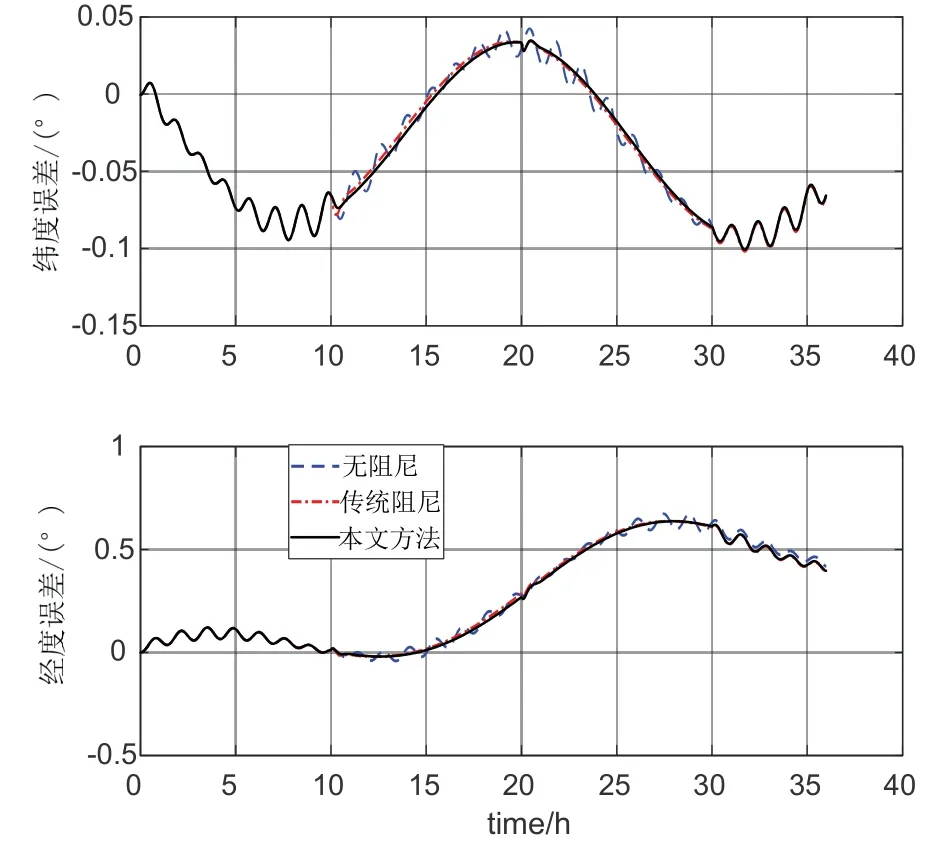
图4 位置误差对比图Fig.4 Position error comparison diagram

图5 失准角对比图Fig.5 Error angle comparison diagram

通过图3～5 三种方法误差曲线的对比，可以看到在第10 小时、第20 小时和第30 小时，因为计程仪提供的外速度参考信息发生变化，各导航参数都产生了超调变化。尤其是第10 小时，系统进行了阻尼状态的切换（由无阻尼状态切换到有阻尼状态），超调较为明显，采用本文方法产生的超调变化小于采用传统阻尼产生的超调变化并且收敛更快。以速度误差为例进行定量分析，在第10 小时系统从无阻尼切换到有阻尼状态时，采用本文方法产生的东向速度误差超调量和北向速度误差超调量分别比传统外速度水平阻尼方法产生的超调量减小13%和15%。

图6 阻尼比Fig.6 Damping ratio

由图6可知，在第10 小时因计程仪判定外速度信息有效，导航系统自动进入阻尼状态，初期阻尼比很大，随后逐渐减小并趋于一个稳定值。在第20 小时，计程仪提供的外速度误差发生变化，系统经过判定仍视为外速度信息为有效信息，但外速度误差的变化会导致阻尼比再次发生变化，当系统再次达到稳态时，阻尼比将再次趋于一个稳定值。通过自适应方法去自动调整反馈增益参数，进而得到对系统更合适的阻尼比，所以此时较小的阻尼比更适合于系统。阻尼比这样的变化过程对惯导系统是有利的，在导航系统初期较大的阻尼比加快了震荡误差的收敛速度，系统稳态时较小的阻尼比有利于载体机动对该系统造成的不利影响。在第30 小时，因为Rk∉［Rmin,Rmax］，所以系统判定计程仪无法提供准确的外速度信息，自动切换至无阻尼状态。

4 结 论

本文以极区航行为背景，针对传统格网惯性导航系统阻尼技术存在的问题，提出了一种自适应反馈增益阻尼方法。利用该方法将原本的控制问题转化为有效估计问题，能够克服传统阻尼网络参数选择的复杂性问题及阻尼网络参数固定的问题。实验仿真结果表明，所提出方法加快了惯导系统误差的收敛速度，能够自主进行不同阻尼状态间的优化切换，而且比传统外速度水平阻尼误差超调量减小了15%左右，提高了系统的导航性能。