基于波叠加法的高速铁路辐射噪声场可视化研究

2020-10-17宋雷鸣张佳宇吴清坤

中国铁道科学 2020年5期

宋雷鸣，张佳宇，吴清坤

（1.北京交通大学机械与电子控制工程学院，北京 100044；2.中车青岛四方车辆研究所有限公司减振事业部，山东青岛 266031）

社会的进步使人们对生活品质有了更高的要求，噪声强弱作为评价环境好坏或产品性能优劣的一项重要指标，噪声评价及减振降噪备受关注。声场可视化能更加形象地给出噪声声场分布特征，掌握声场分布的更多信息，可为噪声评价及减振降噪提供参考［1］。

高速铁路噪声一般由集电系统噪声、轮轨噪声、空气动力性噪声、设备及建筑物噪声等组成。高速铁路辐射噪声声场可视化可清楚地表达高速铁路噪声的传播特性及声场的分布特性，便于从总体及细节2 个方面把握噪声评估及噪声控制对象的特点，提高噪声分析的准确性及噪声控制措施的有效性，为高速铁路减振降噪提供参考。国内外专家学者已就声场的可视化进行了诸多研究。N.Chitanont等［2］利用光学技术对声场进行了可视化研究，Haijiang Zhu 等［3-4］介绍了1 种平面活塞换能器超声场的自动扫描与可视化系统。杨殿阁等［5］使用声全息方法重建运动声源声场后将其与双目视觉测量技术相融合，实现了可视化运动声源声场的目的，可以更加便捷地识别和定位运动声源。孙雪海等［6］通过对水下三维声场的仿真，提出1 种水下声场可视化分析方法，为水下复杂环境的感知提供了重要途径。

作为实现声场可视化的重要手段，声场重构技术逐渐从声源辨识技术中衍生并发展起来。常用的声场重构算法主要有空间声场变换（STSF）常数单元法、Helmholtz方程最小均方误差法（HELS）、边界元法（BEM）以及近场声全息技术（NAH）和波叠加法等。波叠加法自20世纪80年代Koopman等［7］一经提出，便被广泛地应用于辐射声场的计算。Angie Sarkissian［8］提出了1种基于波叠加法的近场声全息技术；Lin Geng 等［9］将时域平面波叠加法拓展应用到瞬态过程的重建过程中，从而为板的振动和声辐射的整体理解提供了重要信息；Y.Xiang 等［10］基于二维快速傅立叶变换（FFT）算法，提出了1 种有效地分析轴对称物体声辐射的复矢径波叠加谱方法。国内对于波叠加法的研究起步较晚，戚茜等［11］研究了基于模态波叠加法的简支平板辐射声场重构，杨殿阁等［12］提出的动态波叠加技术将波叠加理论拓展至运动声源辨识领域；周思同等［13］利用船舶自带拖曳阵回转的方式，采用波叠加法重建了船舶的辐射声场；吴清坤［14］依据波叠加理论，介绍了适用于高速列车声场的重构技术，将以波叠加法为基础的声场重构技术引入到高速铁路领域。

波叠加法理论假定任一辐射体发出的辐射场都可等效为存在于物体内部的若干数量的虚拟声源产生的叠加声场［15］。通过对离散化波动方程的推导，可以确定位于声场内任一位置处的声压。该方法计算精度高、求解速度快，且无须考虑积分的奇异性问题，因此本文应用此方法进行高速铁路的声场可视化研究。

在波叠加理论的整体框架下，通过分析车辆运行时高速铁路辐射噪声的声源特性，引入偶极子声源模型及多普勒校正，得到1个新的方程组并进行求解。同时，将改进的波叠加理论应用于高速铁路的可视化声场重构技术中，效果达到了预期目标，从而使该技术成为研究高速铁路辐射噪声声场的1种新手段。

1 高速铁路噪声声场可视化理论

1.1 波叠加声场重构原理

基于波叠加理论（WSM）的声场重构示意图如图1所示。假定将m个麦克风布置于声辐射体的外部区域中，通过数采设备采集m个麦克风的声压值，接着计算出复声压，利用置于辐射体内部D区域的虚源面（S’）上n个虚源点（m≥n用来保证有唯一解）来近似等效辐射体表面（S）上的声源，计算出虚拟声源点源强，最终依据虚拟声源的源强重构整个声场，进一步可求得辐射物体外部区域中任何一点的声压或其它声学参数。

图1 基于波叠加理论的声场重构示意图

U点处声压p(U)的计算公式为

式中：i2=-1；ρ为空气密度；ω为声波的圆频率；σ代表等效声源源强密度且大小未知；G(U，Q)为自由场条件下的格林函数。

其中：K为波数；R=|U-Q|，R表示辐射体外部测点U到辐射体内部虚拟声源平面上虚源点Q的距离，满足

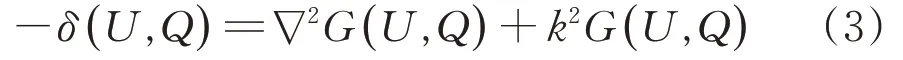
式中：δ代表Dirac函数。

利用式（3）就可通过波叠加理论计算声辐射相关问题。

利用式（1）能够重构静态声源的辐射声场。对于运动声源乃至高速运行的列车，多普勒效应不可避免地会导致时域信号的畸变，产生虚假声源。为解决运动声源辐射场产生的问题，需要进行多普勒效应的校正研究［16］。

1.2 多普勒效应校正

在静止的介质中，当声源的前进方向相交于麦克风与声源之间的连线时，声源的发生频率与麦克风收集到的频率之间会出现偏差而产生多普勒效应，严重影响实验分析结果。多普勒效应产生的机理如图2所示。在图2中，空间固定坐标系xyz中存在声源点gk，麦克风mi到声源点gk的连线与gk前进方向的夹角为θ，且θ是与时间t有关的函数；v为声源运动速度。

图2 多普勒效应产生机理

假设f0为声源点gk的发声频率，f为麦克风mi接收频率，则它们满足关系式

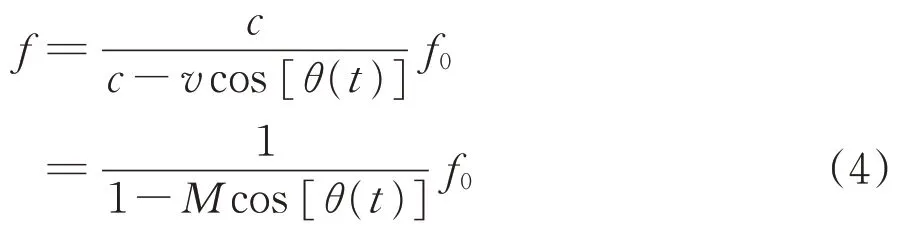
式中：c为声速；M为马赫数。

设(xk(t)，yk，zr) 为声源点gk的坐标，则cos [θ(t)]可表示为

在部分不同夹角下，麦克风接收频率与声源的1/3倍频程中心频率见表1。由表1可知，当麦克风与声源点的连线相交于声源点前进速度方向时，麦克风采集的信号频率因与时间t和声源点gk的位置有关而呈现出非线性变化。

表1 1/3倍频程中心频率的多普勒校正对应表

1.3 波叠加方程的多普勒校正

在实测环境下，声阵列固定在高速铁路旁，当高速列车通过时其位置变化影响着麦克风与声源之间的相对速度。而在高速运行状态下，高速列车通过测量区域的速度快，因此，测试的有效时间短。为计算方便，在较短的有效测试时间内，假设高速列车运行速度不变，即M为常数。在某个确定的时刻t，声阵列测得的固定频率f所对应的声源频率f0可表示为θ的函数，即

由声场重构理论可知，传递函数H与虚源点（虚源面上的单元格）频率f0具有一一对应的函数关系。那么，向离散化的波叠加方程组中增加1个频移函数T是切实可行的，这是因为在实际测试中，多普勒效应产生的信号畸变经常以频率的偏移现象出现。因此，增加的频移函数可使运动声源的波叠加方程在频域上得到校正，从而消除多普勒效应，则波叠加方程可表示为

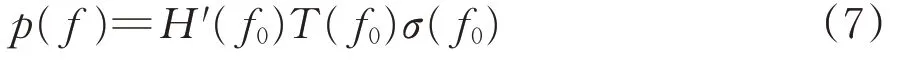
为计算方便，令

则

基于以上分析，运动声源的波叠加方程可用求解常规波叠加方程的方法来计算。

1.4 高速铁路噪声声源配置

当车辆在线路上行驶时，铁路的辐射噪声以列车轮轨区域噪声为主（桥梁噪声很小可忽略不计）。理论研究和工程试验都验证了车轮产生的噪声符合偶极子声源的特质，因而可用偶极子声源模型等效轮轨区噪声［17］。

车辆表面可近似看成刚性的，即单极子源噪声近似为零可忽略不计。在噪声辐射功率方面，气动噪声中四极子源与偶极子源的比值正比于马赫数的平方，而高速列车运行速度与声速相比较低，马赫数较小，因此可忽略四极子源辐射噪声，则列车车表区域的气动噪声［18］可视为由偶极子源产生。

列车高速运行工况下受电弓会产生十分强烈的噪声，包含电弧噪声、弓网摩擦噪声和气动噪声［19］，其中气动噪声为列车受电弓噪声的主要组成部分，因此高速列车的受电弓区域辐射噪声可用偶极子声源配置。

偶极子声源采用正弦函数模拟，列车运行噪声的声源位置应用地面声阵列的声源识别数据进行配置。

1.5 方程组的求解

对于偶极子声源，其声辐射具有指向性。为了揭示列车通过时高速铁路声源的辐射方向与辐射源强的关系，假定位于虚源面上各网格点处的声源位置及格林因子都是常量且相互独立，那么离散化的波叠加方程组可表示为

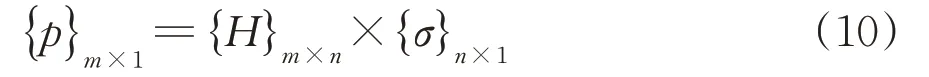
式中：{p}m×1为辐射体外部麦克风阵列采集的各测点声压，{H}m×n为传递函数，与频率和距离密切相关，n为虚拟声源的数量；{σ}n×1为虚拟声源平面上每个虚拟源点的源强。

简化位于车表区域的复杂声源及声场中的诸多传感器，选取任意1个声源和传感器，则列车表面声源示意图如图3所示。

图3 高速列车表面声源示意图

对于第i个虚源点和第j个测点，1≤i≤n，1≤j≤m。θi为虚拟声源点i相对于水平方向的声源指向性夹角，θij为虚源点i到测点j的连线相对于水平方向的夹角，σi为声源源强，则可得到由虚源点位置指向测点位置的源强σij为

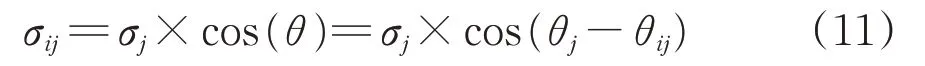
其中，可根据各自位置坐标求得θij，θi表示未知的虚拟源强指向角，那么传递矩阵H可简化为

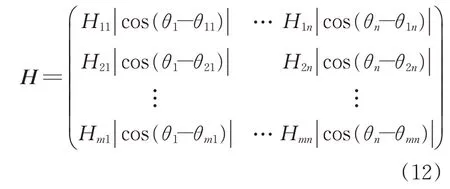
因此，式（12）可用线性方程组的形式表示为

本文利用遗传算法与非线性最小二乘算法相结合完成求解θij。

依据最小二乘拟合算法的原理得到待求误差函数为

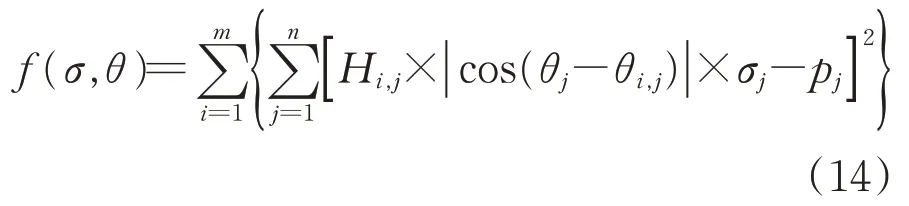
由式（14）不难看出，未知项包含n个虚拟源强σ和n个指向角θ，其优化的最终目标是通过选取适合的源强σ及指向角θ从而最小化误差函数。为了满足解的唯一性原则，虚拟源强数目n与麦克风数目m应遵循关系式m≥2n。

依据遗传算法，设计的计算步骤如下。

步骤1：确定波叠加方程中的待优化对象。显然，虚拟声源源强和声源指向角为待优化的对象。

步骤2：明确优化对象的取值区间。参照经验选择对应于源强最大值为120 dB 的声压，基于偶极子源模型可明确声源指向角变化区间，即

步骤3：编码待优化参数。分别将源强及指向角用8位（依据最终输出选择具体位数）二进制码编码，从而产生2n个自由度，兼具调节性和对误差的决定性，遗传算法的目标就是从中选择最优解。

步骤4：搭建优化模型。由上文推导及式（15）所示的优化对象的取值范围，计算最小值。

步骤5：构建适应度函数。适应度函数对预期结果起着关键性作用，因此适应度函数F取为

α∈(0，1]，α取值视实际情况而定。

步骤6：明确优化算法的基本运行参数。包含：种群规模W；迭代次数A；变异概率Pm；交叉概率Pc；程序调试参数α。确定本文中的各参数为：W=1000，A=1000，Pc=0.7，Pm=0.05，α=0.004。

步骤7：输出最终结果，即优化的虚拟声源的源强和指向角。

2 高速铁路辐射噪声声场重构

由上述理论可知，可以通过求解虚源点参数来达到重构声场的目的，结合频域多普勒校正技术可以重构移动声源的辐射声场。为了验证该理论的有效性，对上述改进的波叠加算法进行编程，并开展高速铁路辐射噪声声场的可视化研究与验证。

2.1 高速铁路辐射噪声声源识别

试验以高速列车通过高架桥路段为例。为了消除背景噪声等因素对结果的影响，有效提升测试分辨率，测试选用双层声阵列。阵列参数见表2。

表2 阵列参数表

选取与线路最为靠近的阵列中心为空间坐标原点。高架桥路段，前阵列距高架桥外边沿8 m。验证测点分别布置前阵列外18 m 和43 m 的小阵列处，即坐标为（0，0，18），（0，1，18），（0，0，43），（0，1，43）m。图4为测试现场布置图，图5为现场测试图。

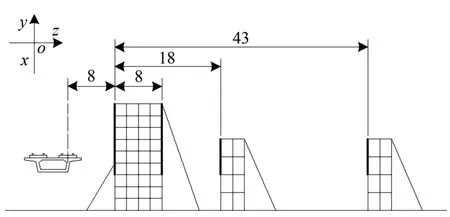
图4 测试现场布置图（单位：m）

图5 测试现场

选取靠近轨道的阵列面为测试基准面，规定z轴正方向为基准面远离轨道的方向，x轴正向为列车前进方向，y轴正向为竖直向上。图6为某高速列车通过时前4节车厢长度内铁路辐射噪声源识别云图。从图6可看出，当列车通过时，虽然列车轮轨区域以下的桥梁区域有部分声源，但高速铁路噪声主要集中在列车轮轨区域及受电弓区域。因此选取声源面大小为：x轴为（0∶1∶200）m；y轴为（-6∶0.1∶6）m。其中y向轮轨区高度为（-0.4∶0.9）m（包含高架桥噪声）；车表区域为（1∶3.7）m；受电弓区间为（3.8∶6）m。通过这种区域划分的方式可以对单一子区域内的辐射噪声场进行可视化重构，掌握该区域的声场信息，提出针对性的降噪方法。由于原理类似，本文只研究列车通过时，整个铁路区域内辐射声场分布。

2.2 高速铁路辐射噪声声场分布及验证

对麦克风采集的数据首先使用PULSE 系统进行声源识别，选用1/12 倍频程中心频率作为计算频率，最低140 Hz 到最高7 100 Hz，共67 个计算频率。挑选车辆完整经过麦克风阵列正前方的时间段内接收的数据为计算声源辨识别和声场重构的最佳数据，以位于或靠近阵列中心的麦克风通道为参考，考虑到列车速度等参数的误差，参考通道出现的对应列车驶近和驶离的2 个峰值前后各5 m 作为计算区段。为了准确地重构声场，将车辆驶过时采集的时域数据按车厢长度划分成8 个模块进行计算，第1、第2 节车厢通过数据为第1 模块，第1、第2、第3 节车厢通过数据为第2 个计算模块，依次递推，第7、第8 节车厢通过数据为第8 模块，规定每1 个计算模块的中部通过阵列中心时计算1次。每次计算时，虚源点都要选择为单一计算频率下的每1个计算模块声源辨识的极大值点，极大值点定义为在可接受的声源辨识分辨率下，某一划分的单元格上的数值高于上下前后单元格上的数值，则此单元格为一个极大值点。一般情况下，筛选出的虚源点数目要小于参加计算的麦克风数目。对于辨识结果中的较小极值点，由于噪声贡献量较小，且可能为虚假声源，故忽略不计。最后，将8次计算的结果做等效连续A声级计算。本测试选取的重构面z向选择为-7 m至+100 m（图中只显示-7～50 m 范围），Y 向选择为-5 m 至+10 m，计算精度为1 m×1 m。

图6 高速铁路声源识别云图

图7为试验用高速列车以310 km·h-1运行时，在主要噪声频段（200 ～6 300 Hz）内声场分布重构云图。从图7不难看出，重构得到的高速铁路辐射噪声声场最大值集中在轮轨区域，且该区域辐射噪声衰减较慢，而受电弓区域辐射噪声衰减较快。

图7 高速铁路辐射声场分布云图

由重构原理可知，重构后得到的声场云图是声源辨识图中各声源辐射得到的结果，反映整个声场辐射噪声的总体状况。选取声场分布图中等值线相距声源最远的点与声源点连成直线，得到整车的声场指向性，见图7中虚线所示方向。不难看出，以整车的辐射噪声声场作为重构对象时，整个区域的声场指向斜上方，声源指向角约为27°。

为了验证该声场重构方法及所编写程序的准确性，选取10 个实测点的数据与重构值进行对比，所选点坐标见表3。从表3中可以看出，验证点分布在4 个距列车距离不同的阵列上。其中，前4 个验证点位于双十字阵列，后6个验证点位于双十字阵列后方的小验证阵列上。

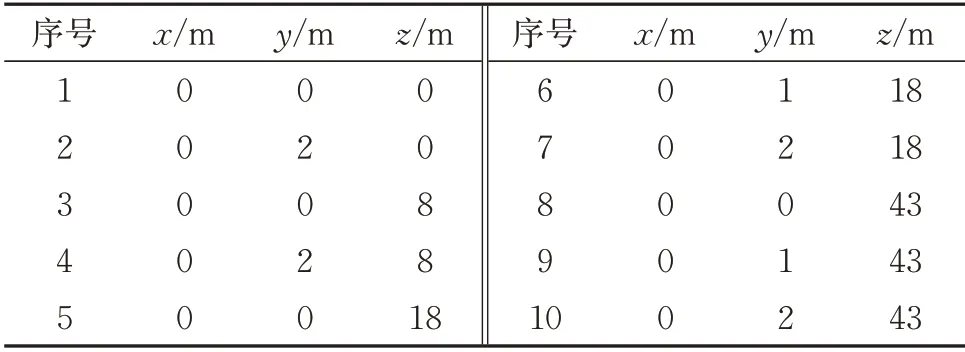
表3 对比点坐标

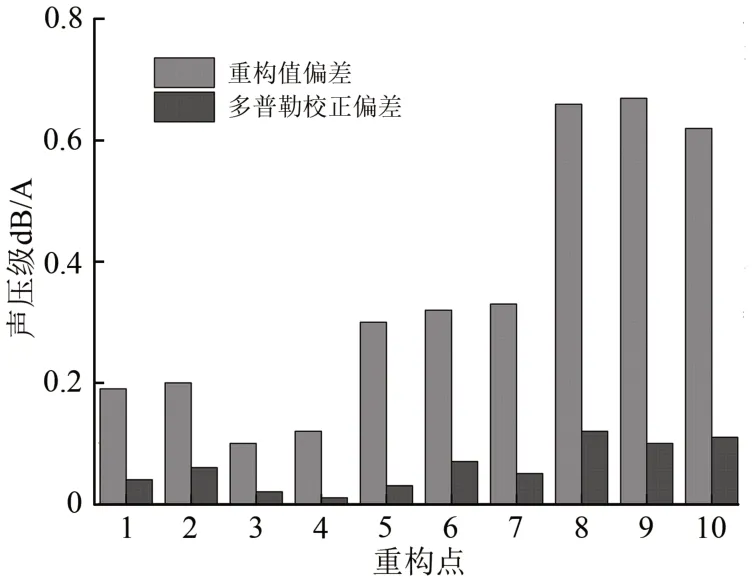
图8 实测与重构数据对比

图8为各测点实测与重构数据对比图。图中，实际值为0 dB（A）。由图8可知，未经多普勒效应校正的重构值与经多普勒修正的重构值与实际值的偏差都保持在0.8 dB 以内，说明重构值符合实际，声场重构效果良好，且基于多普勒修正的声场重构精度较高。但从图中后6 个验证测点不难看出，随着重构距离的增加，重构偏差明显增加，说明声场重构的距离对重构精度有一定的影响。