公轨两用大跨度单索面钢桁梁斜拉桥动力特性研究

曾 勇，曾渝茼，谭红梅，周建庭

（1.重庆交通大学 山区桥梁及隧道工程国家重点实验室，重庆 400074；2.重庆交通大学 山区桥梁结构与材料教育部工程研究中心，重庆 400074）

近年来国内城市道路公轨两用需求增加，公轨两用桥梁成为大城市跨江、跨河桥梁的主要桥型之一。公轨两用大跨度单索面钢桁梁双塔斜拉桥具有造型优美、桥型新颖的特点，又包含公轨两用这一决定性优势，因此成为长江上游流域城市桥梁的热门选择。但其结构复杂性使空间动力特性变得复杂特殊、不具确定性，因而对该桥型动力性能的研究具有重要意义。

桥梁结构的设计参数对于桥梁抗震、抗风、稳定性等动力响应问题有巨大影响。夏志远等［1］对某悬索桥恒载集度的变系数动力分析结果表明恒载集度的变化对悬索桥动力性能具有一定的影响；康俊涛等［2］对某悬索桥的结构刚度进行变参数分析，得出悬索桥各构件刚度对桥梁振型均有影响的结论；周潇等［3］分析了某斜拉桥的自振特性以及桥梁高度、数量的变参数动力性能；康俊涛等［4］虽对桥梁刚度进行了变参数分析，但并未分别将塔刚度、索刚度和梁刚度进行变换对比分析；TOCHAEI Emad等［5］研究了近场地震动和土—结构相互作用对斜拉桥动力响应的影响；WANG Hao 等［6］基于结构健康监测对大跨度斜拉桥台风动力特性进行了研究；文献［7—15］对其他类型斜拉桥动力性能进行了研究。但国内外目前对公轨两用大跨度单索面钢桁梁双塔斜拉桥动力特性的分析尚属空白，公轨两用大跨度单索面钢桁梁斜拉桥的索面布置形式、荷载集度、塔索梁结构刚度、辅助墩数量对桥梁动力特性产生的影响不容忽略，但还没有相关研究。

本文以某公轨两用单索面钢桁梁双塔斜拉桥为例，运用有限元软件MIDAS/Civil 2019 中的子空间迭代法对桥梁振型进行分析，通过改变索面布置形式、整体改变恒载集度、分别变换塔刚度、索刚度和梁刚度以及增设不同数量的辅助墩研究结构参数变化对桥梁动力特性的影响。

1 工程背景

某公轨两用大跨度单索面钢桁梁双塔斜拉桥跨径组合为（225.5+445+190.5）m，桥梁全长为858 m。桥梁为半漂浮体系，梁与塔、台之间分别设抗压支座，两侧边跨支座纵向自由，一侧塔纵向约束，另一侧塔为纵向自由，如图1所示。

图1 某公轨两用大跨度单索面钢桁梁双塔斜拉桥

塔形为天梭造型，两侧塔高分别为162 和172 m，材料为C50 混凝土；梁体为双层钢桁架布置如图2所示，高跨比约为1/38，下层为双线城市轨道交通，上层为公路双线4车道，上下桥面均为正交异形桥面板，因为功能不同宽度为24.50～36.99 m；选择平行钢绞线作为斜拉索，材料为Strand1860。该桥材料物理性能参数见表1。

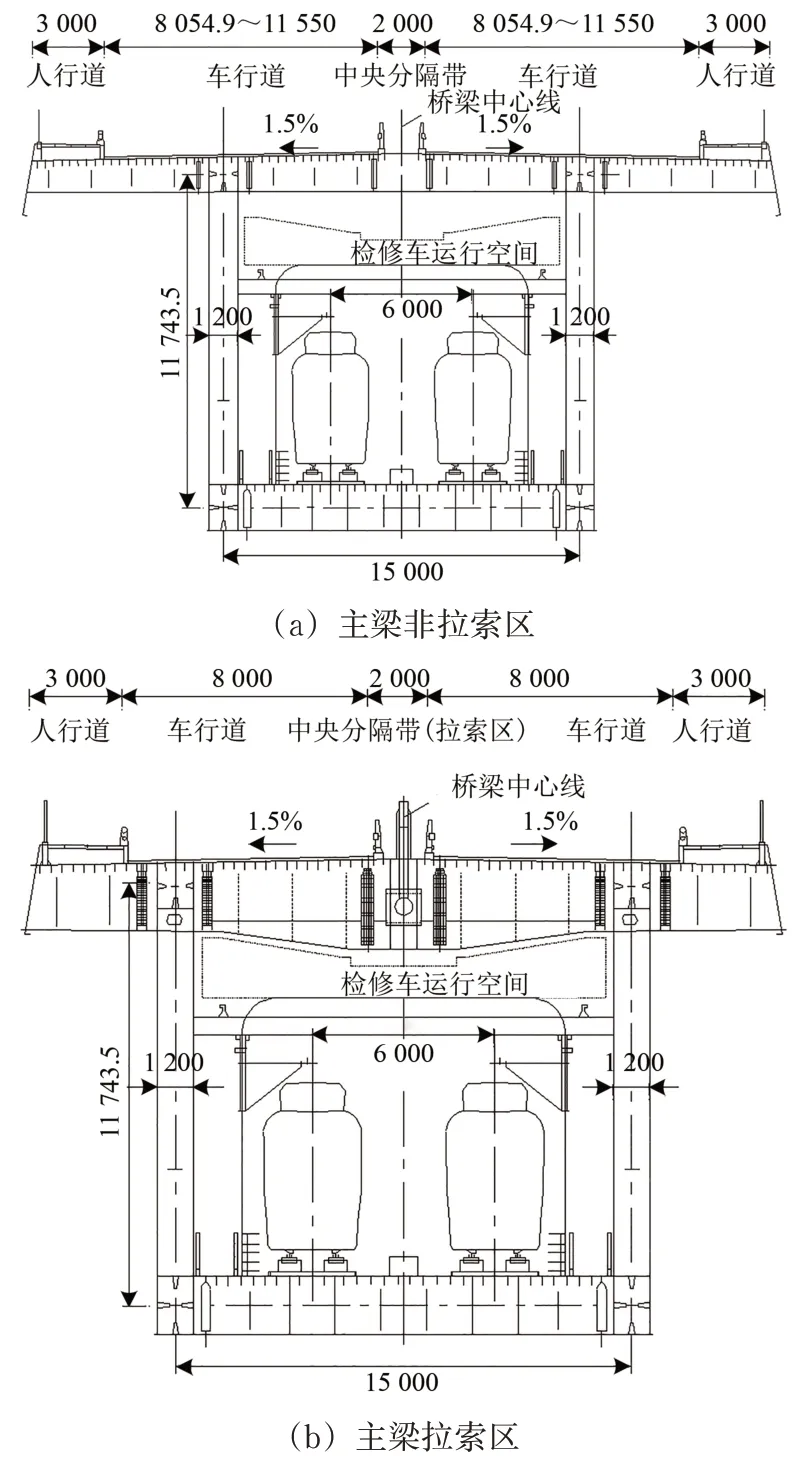
图2 主梁控制断面示意图（单位：mm）

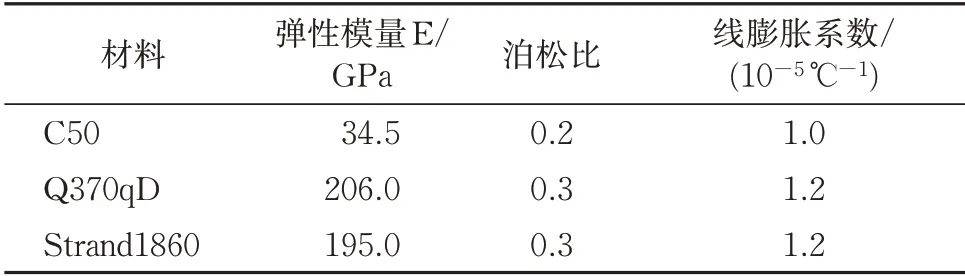
表1 主要材料物理性能参数

2 有限元模型

采用MIDAS/Civil 2019 有限元结构软件建立全桥空间有限元模型，其中塔和主梁采用梁单元模拟，索采用只受拉单元模拟。上游侧左塔和主梁之间设置竖向、纵向和横向支承，下游侧左塔和主梁之间设置纵向和横向支承，上游侧右塔和主梁之间设置竖向和横向支承，下游侧右塔和主梁之间仅设置竖向支承，塔固结在地上，梁的两端与地固结，斜拉索与主梁和桥塔之间均采用弹性连接。建模时考虑所有施工阶段（共62 个），考虑几何非线性效应并采用子空间迭代法进行桥梁振型分析。变换不同的结构参数，建立多个有限元模型，索面布置考虑单索面和双索面，其余参数变化均没有改变结构外观，单索面斜拉桥和双索面斜拉桥的有限元模型如图3所示。

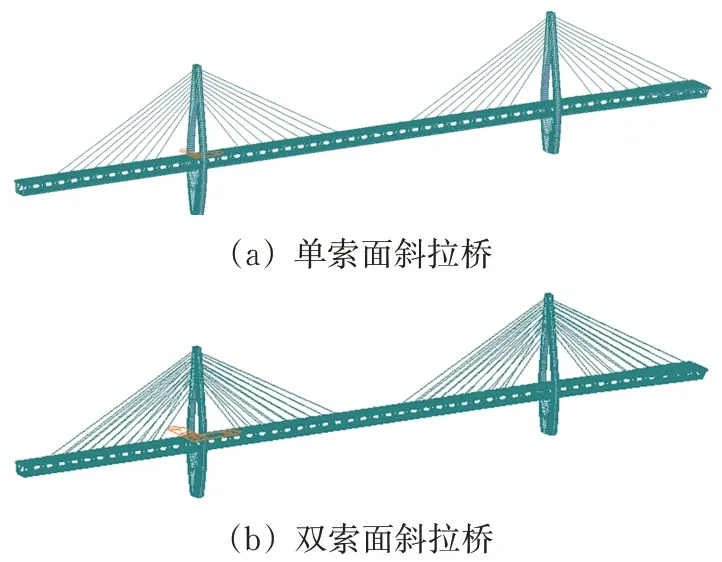
图3 2种桥型的有限元模型

3 动力特性参数

3.1 索面布置对动力特性的影响

采用子空间迭代法对桥梁振型进行分析，得到公轨两用大跨度单索面钢桁梁双塔斜拉桥以及双索面斜拉桥的10 个模态振型，其特性见表2。由表2可知以下结果。

（1）对于前5 阶模态，单索面斜拉桥与双索面斜拉桥的频率和周期有所不同，但振型形态一致。当振型形态为弯扭耦合时（第4 阶模态），双索面斜拉桥的频率大于单索面斜拉桥，这是因为单索面斜拉桥的斜拉索无法承受偏心荷载引起的扭转，而双索面可以增强斜拉桥的抗扭刚度。原结构基频为0.243 Hz，第1 阶模态振型为梁中跨1 阶横弯，此为桥梁的基本振型，表明单索面钢桁梁双塔斜拉桥的横向抗弯刚度较小；第2 阶模态振型为1 阶对称竖弯，振型出现较早，证明该桥纵向抗弯刚度较低，横纵向抗弯刚度均较低的情况下，应对桥梁抗风稳定性问题产生重视；第4阶模态的振型出现了梁的弯扭耦合，可见该桥的抗弯和抗扭能力较为均衡且较弱，对桥梁抗风稳定性较为不利。

（2）对于第6 阶—第10 阶模态，双索面斜拉桥每阶频率均大于单索面斜拉桥，从第6阶模态开始，振型形态有所不同。在第6阶时，单索面斜拉桥主梁出现了3 阶对称竖弯，但双索面斜拉桥为2阶对称竖弯振型；第7 阶—第9 阶模态为弯扭耦合振型，单索面斜拉桥的扭转程度较大，双索面斜拉桥的扭转程度较轻微，证明双索面布置可以改善钢桁架斜拉桥的扭转特性，振型对比如图4所示。

（3）单索面钢桁梁双塔斜拉桥属于半漂浮体系，桥梁整体较柔，有利于减少地震反应，但从振型特点看来，单索面的设计使得桥梁具有较弱抗扭刚度，对于抗风稳定性极为不利。将单索面布置改为双索面布置，钢桁梁双塔斜拉桥扭转刚度有所提升，可以从一定程度上避免弯扭耦合的发生，增强桥梁抗风稳定性。

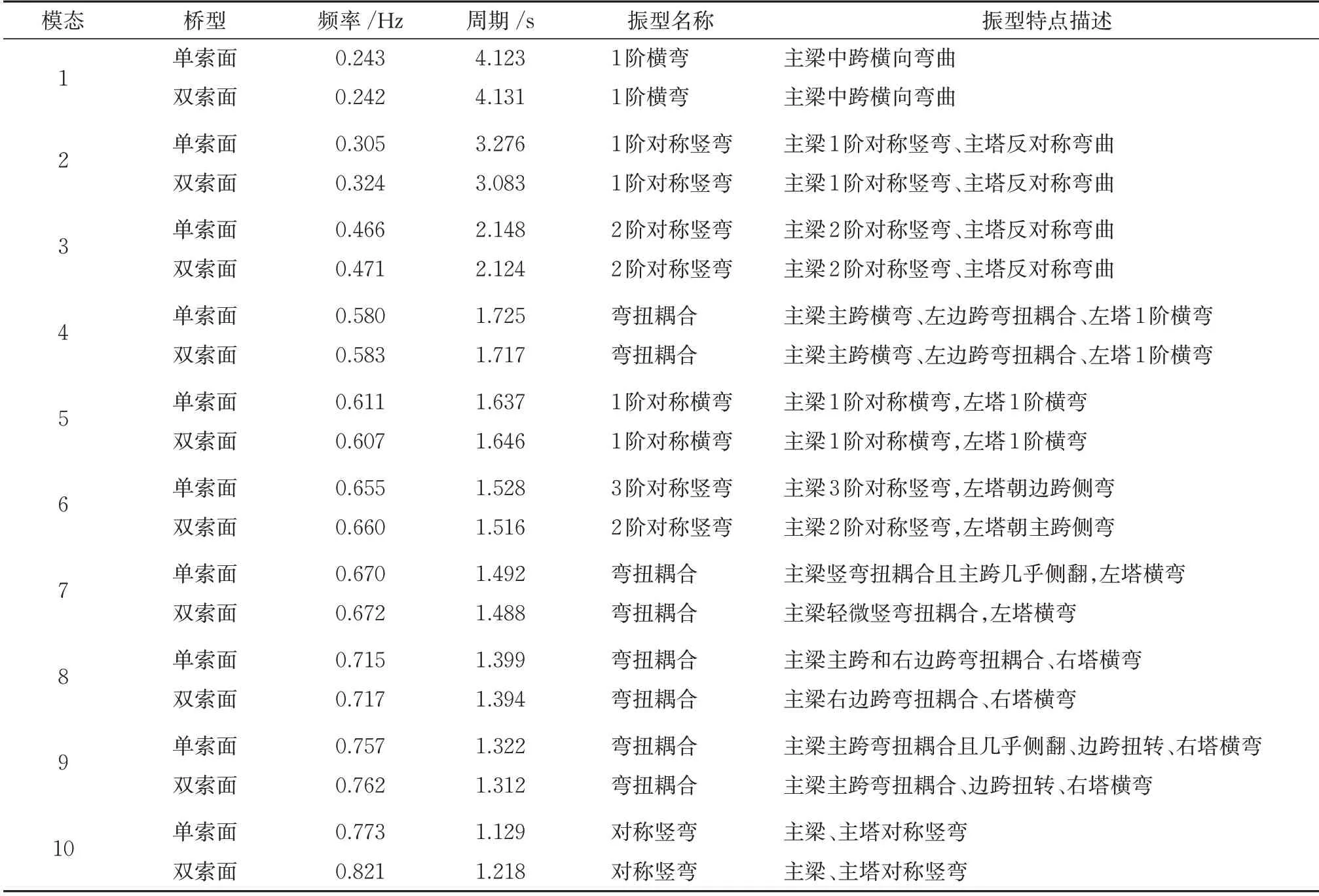
表2 主要振型特性

3.2 结构参数对动力特性的影响

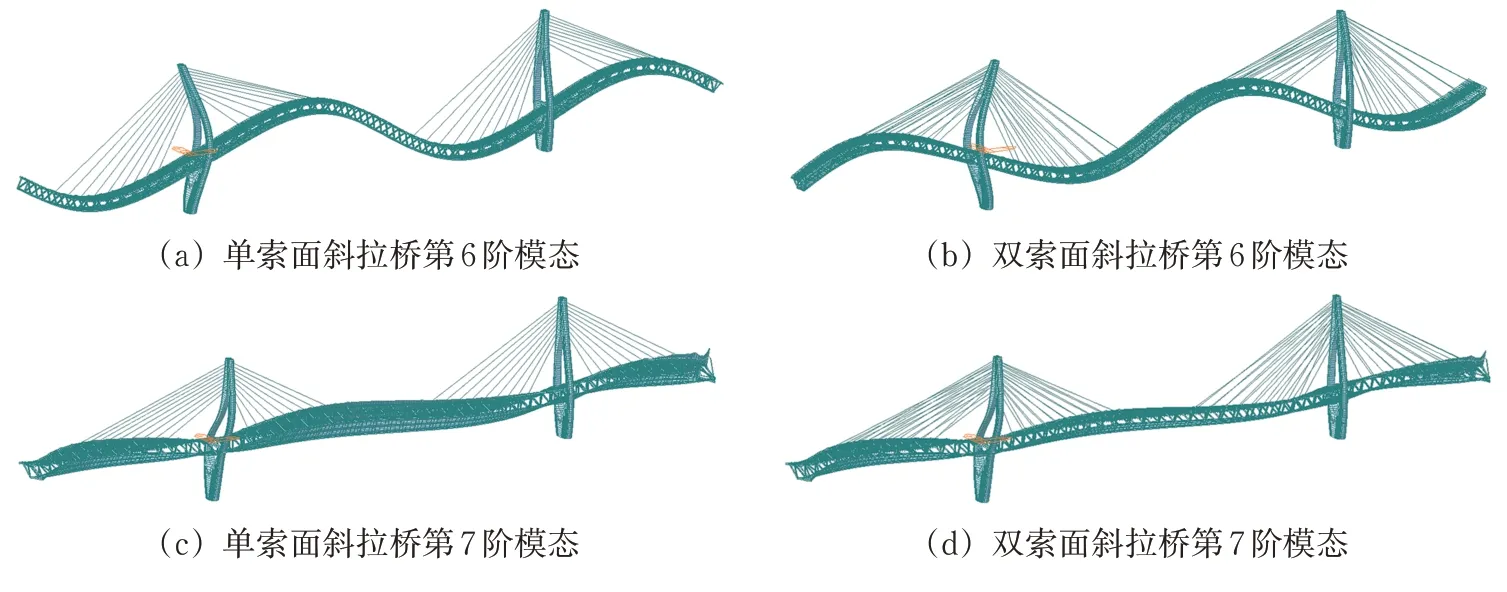
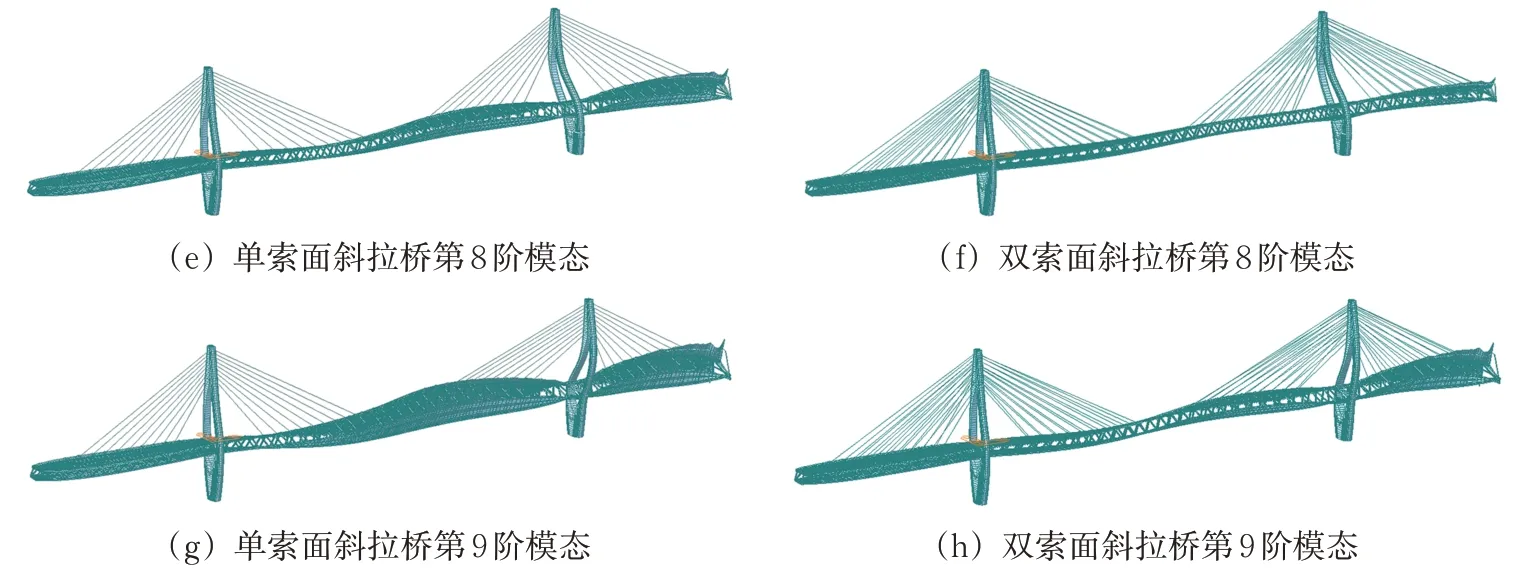
图4 2种桥型的振型对比图

为寻找提高公轨两用大跨度单索面钢桁梁双塔斜拉桥抗风稳定性并保持其良好的抗震能力的措施，对桥梁恒载集度进行整体变换、塔刚度、索刚度和梁刚度进行分别变换以及在桥梁两端分别增置不同数量的辅助墩，研究其动力特性的变化情况。因为并没有改变桥梁的结构体系，因此主要对前5阶模态的振型频率进行分析，以下用f1—f5表示前5阶模态。

3.2.1 恒载集度

将恒载集度进行整体变换，变换系数分别为0.6，0.8，1.0，1.2，1.4 和1.6，进行分析。观察恒载集度变换后的桥梁振型形态，发现恒载集度变换不会对桥梁振型形态造成影响。图5给出了前5阶主要模态自振频率随恒载集度的变化情况。

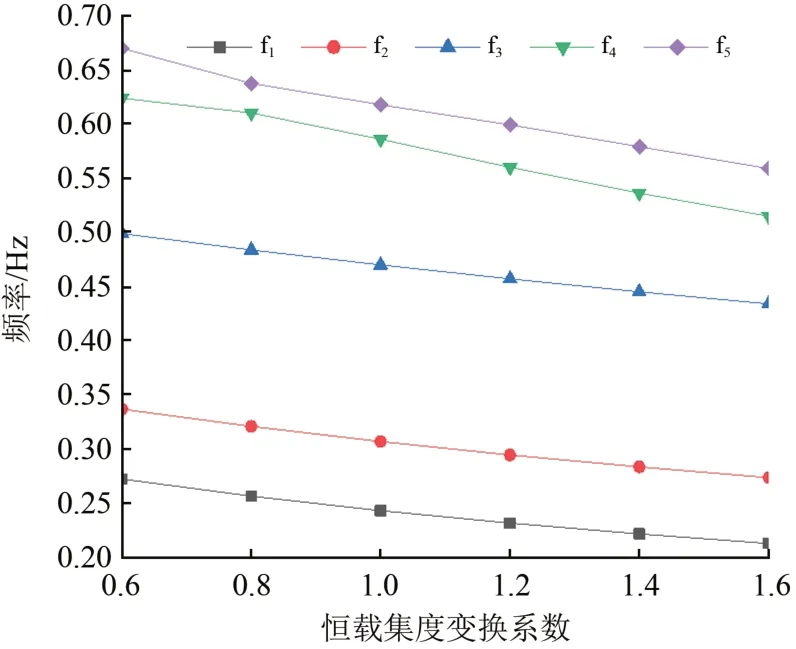
图5 恒载变化对前5阶频率的影响

由图5可知：随着恒载集度系数由0.6 增加至1.6，该桥5 个模态的频率都呈下降趋势，且下降的程度基本一致，恒载集度的变换对于5个模态频率的影响程度相当，其中下降幅度最大的为第1阶模态，达到了21.6%，由此可见恒载集度的增加对桥梁抗弯、抗扭、抗弯扭耦合均不利。为保证桥梁的抗震、抗风稳定性桥梁设计应该尽量选择合理轻型材料作为桥梁的二期恒载。

3.2.2 结构刚度

将塔、索和梁的刚度系数分别变换为0.6，0.8，1.0，1.2，1.4 和1.6，研究刚度变化对该桥动力性能的影响。分析塔、索和梁的刚度变化后的振型形态，发现塔、索和梁的刚度变化虽然对桥振型形态有一定影响，但影响程度不会对研究结论有决定性作用。

1）塔

保持其他构件刚度不变，取塔的刚度变换系数为0.6，0.8，1.0，1.2，1.4 和1.6，研究5 个主要振型模态，其结果如图6所示。

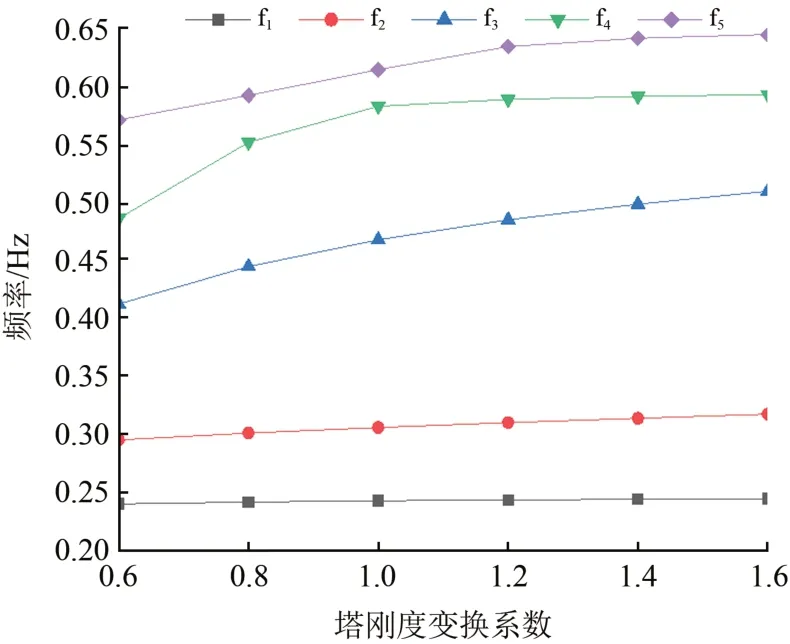
图6 塔刚度变化对前5阶频率的影响

由图6可知：随着塔的刚度系数从0.6 上升至1.6，该桥前5 阶模态的频率都呈上升趋势，其中上升幅度最大的为第3阶模态，达到23.5%，由此可见调整塔的刚度会对桥梁抗震、抗风稳定性能力造成明显影响，桥梁设计时可以适当提高塔的刚度以提升桥梁抗震、抗风稳定性。

2）索

保持其他构件刚度不变，将索的刚度变换系数为0.6，0.8，1.0，1.2，1.4 和1.6，研究5 个主要振型模态，结果如图7所示。

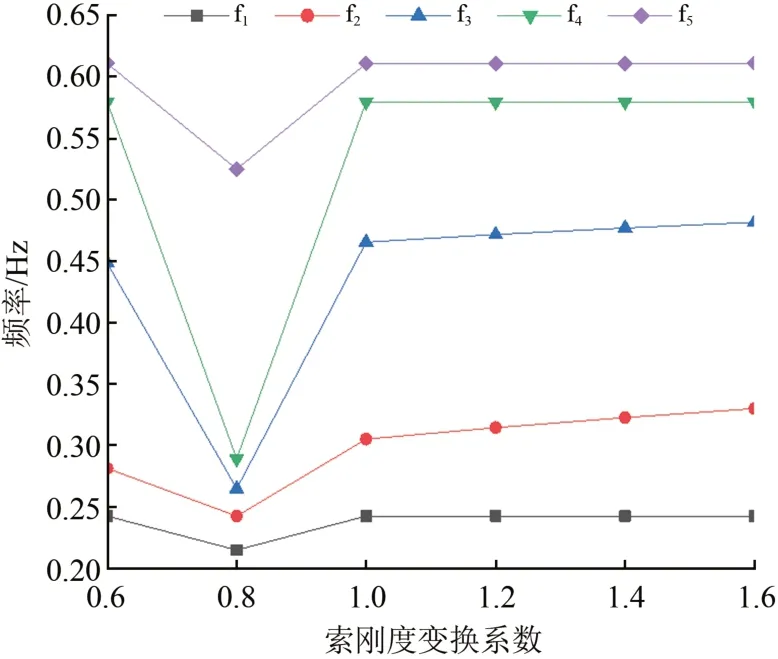
图7 索刚度变化对前5阶频率的影响

由图7可知：索刚度系数为0.8 时，5 个主要模态频率都发生了突降，原因是索刚度系数为0.8时振型形态由索刚度系数1.0 时的中跨1 阶横弯变为中跨1 阶竖弯（如图8所示）；排除索刚度系数0.8 这一特殊情况，随着索的刚度系数从0.6 上升至1.6，该桥前5 阶模态的频率都呈上升趋势，但是除了2阶模态上升幅度为17.3%，其余最高都不到1%。由此可见，由原设计为基准，索刚度的变化对桥梁动力特性影响较为复杂，索的刚度由基准下降的时候，桥梁的动力特性会可能发生较大变化，因此在桥梁设计调整索的刚度可能会对桥梁动力特性产生较大影响，从而对桥梁抗震、抗风稳定性产生影响。

图8 索刚度系数0.8时基频模态

3）梁

保持其他构件刚度不变，将梁的刚度变换系数0.6，0.8，1.0，1.2，1.4 和1.6，研究5 个主要振型模态，结果如图9所示。

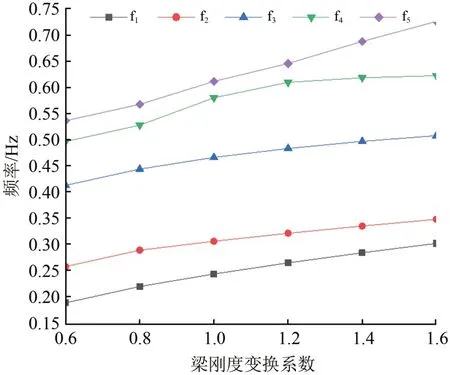
图9 梁刚度变化对前5阶频率的影响

由图9可知：随着梁的刚度系数从0.6 上升至1.6，该桥前5 阶模态的频率都呈上升趋势，其上升幅度最小的是第3阶模态，为23.1%，最大的是第1 阶模态，为60.7%；虽然随着梁的刚度上升，基频发生了较大的变化，与索刚度变化不同的是振型形态没有发生变化。由此可见，对于公轨两用大跨度单索面钢桁梁双塔斜拉桥，对主梁刚度进行适度调整可以优化桥梁抗震、抗风稳定性，在设计时可以对主梁刚度进行最优化设计。

3.2.3 辅助墩数量

由于该桥左边跨大于右边跨，分别设置辅助墩数量从1到6，辅助墩数量为1时是左边跨设置1个辅助墩，数量为2 时是在左右边跨分别设置1 个辅助墩，数量为3 时是在左边跨设置2 个辅助墩右边跨设置1个辅助墩，以此类推，研究其辅助墩数量对桥梁动力特性的影响，结果如图10和图11所示。

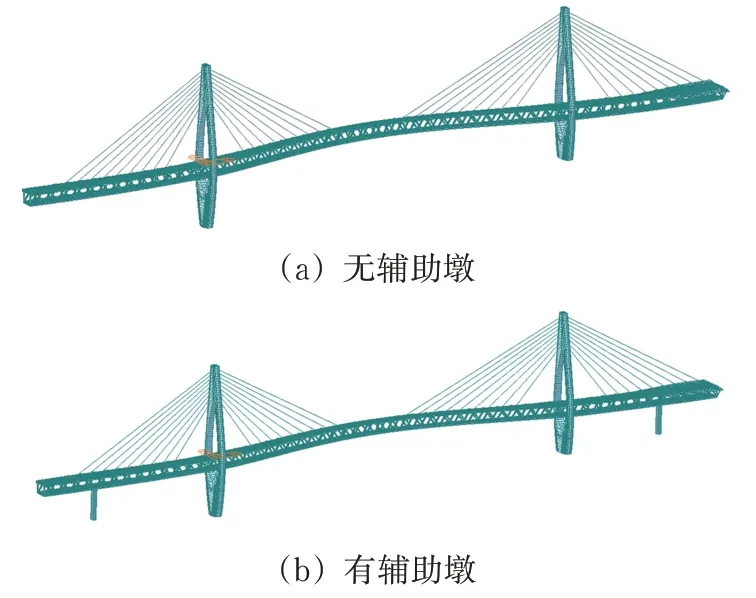
图10 有无辅助墩时斜拉桥基频模态

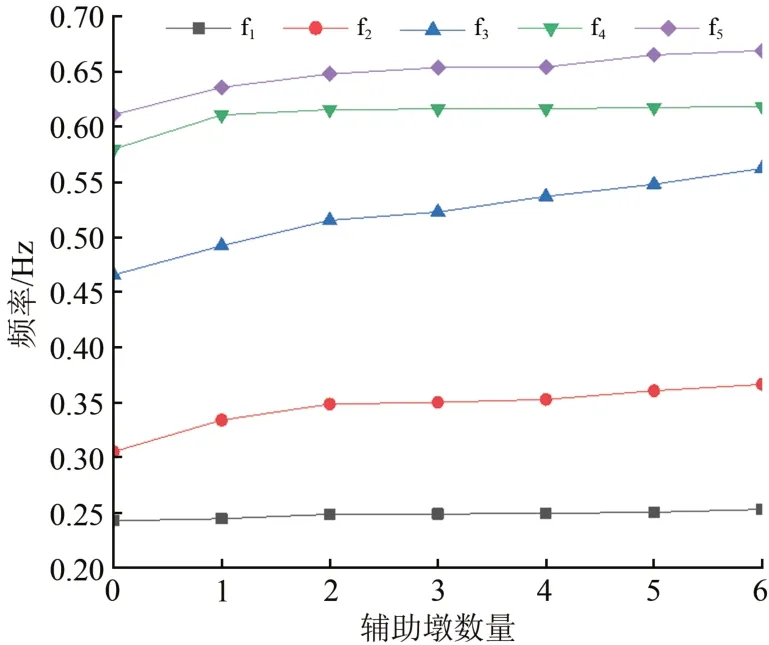
图11 辅助墩数量变化前5阶频率的影响

由图10可见：辅助墩的位置、数量变化不会对桥梁基频产生影响。由图11可知：随着辅助墩的数量从0 个上升至6 个的过程中，该桥前5 阶模态的频率都呈上升趋势，其上升幅度最小的是第1阶模态，为3.5%，最大的是第2阶模态，为14.3%，但其振型形状并未发生变。由此可见，在公轨两用大跨度单索面钢桁梁双塔斜拉桥上设置辅助墩可以提高其抗弯、抗扭能力，对桥梁的抗震、抗风稳定性是有利的，在桥梁设计中可以适当通过增加辅助墩的方式来加强桥梁的稳定性能，但个数大于2后，各振型的频率的增加有限。

4 结 论

（1）单索面钢桁梁双塔斜拉桥抗弯抗扭刚度均衡且较弱，对桥梁抗风稳定性较为不利，但由于其为半漂浮体系，对减少地震响应能力有所提升；双索面斜拉桥的抗扭刚度大于单索面斜拉桥，将单索面布置改为双索面布置，可以在一定程度上避免弯扭耦合振型的出现，增强抗风稳定性。

（2）恒载集度的增加对于桥梁抗弯、抗扭、抗弯扭耦合均不利，为保证斜拉桥的抗震、抗风稳定性桥梁设计应该尽量选择较轻的二期恒载。

（3）提高塔和梁的刚度可以增加桥梁抗震、抗风稳定性；索刚度的变化对桥梁动力特性影响较为复杂，0.8 倍斜拉索刚度时桥梁的振型形态发生较大变化，因此在桥梁设计调整索的刚度可能会对桥梁抗震、抗风稳定性造成较大影响。

（4）设置辅助墩可以提高公轨两用大跨度单索面钢桁梁双塔斜拉桥抗弯、抗扭能力，对桥梁的抗震、抗风稳定性有利，在桥梁设计中可以适当通过增加辅助墩的方式来加强桥梁的动力性能。