面向雷达数字化设计与仿真的杂波模拟方法研究

2020-10-16卢冀黄超王蒙

火控雷达技术 2020年2期

关键词：数字地图杂波雷达

卢冀黄超王蒙

(西安电子工程研究所西安 710100)

0 引言

仿真雷达模型同目标、杂波、电子干扰等模型的相互作用是雷达数字化设计与仿真系统的核心功能[1-2],面对杂波模拟这一雷达技术领域的经典问题[3], 探索适用于雷达数字化设计与仿真系统的杂波建模方法，面临着新的问题：

1)如何基于统一的雷达模型同目标、杂波、电子战模型的接口[2]，描述雷达波形同杂波相互作用后的参数及其变化，以通过仿真真实且高效地反映雷达与杂波相互作用的结果；

2)如何构建面杂波和体杂波模型，满足雷达数字化设计与仿真系统的应用需求，即杂波模型具有较好的仿真需求适用性和与数字化系统的兼容性。

本文将围绕上述问题，系统性地探索雷达数字化设计与仿真中的杂波模拟技术和具体实现方法，为数字化雷达杂波模拟的实现与技术发展起到抛砖引玉的作用。

1 总体架构

基于雷达波形与目标、杂波、电子战模型交互的参数[2]，雷达与杂波相互作用涉及的参数见表1所列。其中p,f,φ0,t0,δAz和δEL(τ的变化一般可忽略)发生变化，其余参数将用于杂波模型中相关参数的计算。

表1 雷达波形参数

双程杂波链路的功率变化Δp为

(1)

c表示光速，R表示杂波距离，η=σejφ表示杂波RCS。数字化仿真中，R为

(2)

Ru为不模糊距离，即

(3)

R取决于杂波类型，面杂波时R是目标距离，体杂波时根据雷达与杂波位置即可计算。

双程频率偏移Δf为

(4)

其中vrel表示雷达相对目标视线速度。

双程相位变化Δφ为

(5)

一般情况下，因地形复杂，面杂波时φ=0。

双程时延变化Δt为

(6)

显然，回波的俯仰达到角与入射角度分别为δAZ+π和-δEL。

p,f,φ0,t0,δAz和δEL的变化根据表1所列参数，及上述说明和式(1)～式(6)即可计算得到，杂波模拟的η=σejφ，即杂波RCS，将通过杂波模型计算。当获得杂波回波参数后同目标回波一样，即可获得杂波回波波形[2]。

2 杂波模型构建

2.1 面杂波模型

面杂波主要考虑σ值，满足

σ=σ0·S

(7)

其中σ0为单位后向散射系数，一般由经典的数学模型得到或电磁计算方法得到，S为杂波区域面积。面杂波模型的处理流程见图1所示。

由图1可知，杂波区域面积S跟雷达、目标参数相关。雷达大地坐标系下的坐标为(RxRyRz)，目标为(TxTyTz)，那么

判断1：

(8)

vR表示雷达速度。

判断2：

(9)

其中vrel和vres分别表示视线速度和速度分辨率，则

(10)

(11)

判断3：擦地角α的计算见式(12)。

(12)

其中ae为地球半径。

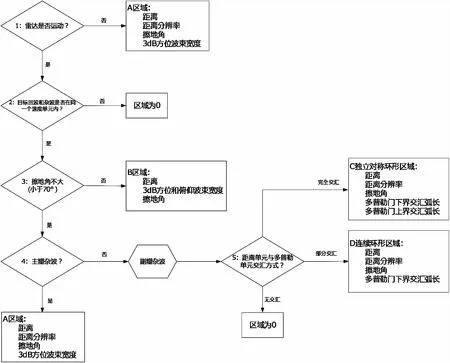
图1 面杂波模型的处理流程

判断4：

(13)

其中δAz|A和δEl|A表示天线波束方位角和俯仰角，θ和φ表示天线方位和俯仰波束宽度，δAz|C和δEl|C表示雷达视线方向的杂波方位角和俯仰角，则

(14)

(15)

其中R*表示雷达到杂波距离，则杂波为主瓣杂波时

(16)

在杂波为旁瓣杂波时，统计最近不模糊距离的杂波，此时

(17)

判断5：距离与多普勒单元交汇说明见图2所示，此时可分为三种情况，见表2说明。

由图2，相关参数计算为

RL=R-mod(R,Rres)

(18)

其中R满足公式(19)。

(19)

图2 距离与多普勒单元交汇说明

表2 距离与多普勒单元交汇情况

RU=RL+Rres

(20)

Rres表示距离分辨率，则

(21)

RU|G=RUcosαc

(22)

其中Ru|G表示Ru在地面的投影，αc表示杂波区域的擦地角，则

(23)

另有

(24)

其中

(25)

其中fu(fDop_U)表示多普勒分辨率上界，fu可由fl(fDop_L)计算

(26)

fres表示多普勒分辨率，则

(27)

fu=fl+fres

(28)

另有

(29)

其中

(30)

由式(22)，式(24)和式(29)的结果，xu和xl可以计算为

(31)

yu和yl为

(32)

由式(31)可得xu，xl。

A区域宽度W是杂波距离经方位角在杂波区域的投影，则

(33)

杂波区域长度L是距离分辨率经擦地角放大后的长度，则

(34)

杂波区域面积S=WL，即

(35)

B区域是3 dB波束形成的椭圆经擦地角在杂波平面的散布，即

(36)

a和b分别是杂波距离在方位和俯仰上投影的距离，则

(37)

C区域近似为S=WL，W由式(33)计算，L为连续环形区域的弧长，可由xl和yl对应的弧长表示，则

(38)

(39)

D区域近似为S=WL，W由式(33)计算，L为独立对称环形区域的弧长，可由xl和yl对应的弧长减去xu和yu对应的弧长来表示，则

(40)

(41)

σ0计算是雷达技术领域研究的经典问题，即用更精确的数学模型逼近真实的不同地表的散射系数，在数字化设计与仿真系统中，计算σ0方法的构建应遵循以下几个条件：

1)系统性：频率支持范围宽，地形类型多样化，考虑动态变化和相关性，数据真实度高；

2)兼容性：地表类型能与数字地图匹配，接口与功能实现易于数字建模与仿真。

在已有研究成果中，WMOC模型[4]支持L到W频段，通过经典的GTI海杂波模型[6]满足高擦地角计算需求，采用威布尔分布匹配不同地形的实际杂波，且通过大量试验优化与验证了模型的有效性，并能有数字地图进行良好的匹配[5]，易于编程实现，适用于雷达设计与仿真系统，其伪代码见图3所示。

图3 WMOC模型伪代码

由图3可知，WMOC模型计算σ0时，需要知道地形，即进行数字地图与地表类型的匹配，根据雷达波形参数和数字地图信息，易得波束在地图中的位置，那么可根据该位置的地图信息解算地表类型。

数字地图由像素点构成，设某一个区域M×N点阵组成，其中任一点的颜色可以表示成[r,g,b])mn，r,g,b表示红绿蓝颜色分量，m=1,…,M;n=1,…,N。需要识别的地形可以用不同颜色来描述，那么第i种被识别的地形可以描述为(Ri,Gi,Bi)，i=1,…,I，识别标准可以为

(42)

以某小区数字地图为例，论文方法识别结果见图4所示，在城市区域，当识别采用分辨率较小时，可以识别植被、草地、灌木、岩土等类型，随着分辨率的增加，该区域都被识别为城市，与实际情况基本相符。

获得地形后，再根据雷达工作频率，擦地角、天线极化，即可由图3方法获得σ0，根据计算得到的S和式(7)获得杂波RCS值σ0。

2.2 体杂波模型

在数字化设计与仿真系统中，体杂波与目标建模的方法基本一致，具体见雷达与目标建模方法研究[2]，然而，体杂波作为非感兴趣目标大都受自然条件影响而变化，以典型箔条杂波为例，其空间信息和RCS受风速和自身形态参数的变化而变化[8]，具体见表3所列。

图4 数字地图地表类型识别

表3 箔条空间信息及RCS信息

(43)

(44)

其中Ca是降速系数，vwx|t和vwy|t分别是风的x向和y向速度，易从风速和风向计算，那么箔条在t时刻位置Cx|t和Cy|t的计算方法是

(45)

(46)

箔条在t时刻的高度Cz|t的计算方法是

(47)

其中vz表示箔条下降速度。

箔条RCS的静态值一般由电磁计算获得(此处考虑杂波半径，即体积)，并通过文件导入数字化系统，其动态起伏和角闪烁与其他目标计算及生成方法一致[2]，但箔条RCS的幅度变化还需考虑另外两个因素：

1)自身的膨胀和稀疏，由此产生的RCS幅度衰减Δσ，其计算方法一般为

(48)

其中Cb和Cs分别为膨胀系数和稀疏系数。

2)杂波起伏具有时空相关性，即起伏变化概率模型生成的随机数具有时间和空间相关性，在数学模型中要考虑时间和空间的相关性系数。例如图5，在Matlab/Simulink中考虑高斯分布的随机数参数Sampletime以设置相关性。

图5 相关性设置

3 仿真结果

杂波σ0的仿真验证了WMOC模型在数字化雷达设计与仿真的可用性和有效性，天线水平极化，风向45°，风速10 m/s，频率分别设为2 GHz(L频段)和12 GHz(X频段)，基于图3所示WNOC模型进行了建模与仿真，表4列出了不同擦地角和地形时，单次仿真得到的σ0值模型中采用随机数来描述威布尔分布的参数，因此单次仿真的σ0跟擦地角并无较好的线性关系，但表4结果与WMOC模型结果[5]变化趋势基本一致。

表4 杂波σ0仿真结果(dB)

箔条仿真参数，箔条抛洒时刻第1 s，抛洒平台的坐标(100,100,200)，单位m，风向为45°(东北风)，风速为10 m/s，箔条RCS幅度为固定值30，相位为0，下降速度2 m/s，降速系数为10-5，膨胀系数10，稀疏系数10，相关系数0.1s，图6显示了0～120 s内箔条位置和0～2 s内姿态的变化，风速和风向产生X和Y值的变化，并在抛洒时刻产生方位和俯仰角度，降速系数和下降速度产生Z值的变化。图7显示了0～120 s内随着箔条运动RCS幅度的变化，结果均与实际情况相符[8]。

4 结束语

针对雷达数字化设计与仿真系统，从杂波仿真功能入手，基于统一的雷达与目标、杂波、电子干扰等模型的参数化接口给出了雷达模型同杂波模型的接口参数，并详细给出了陆、海面杂波及箔条体杂波模型的构建方法。本文较为系统地阐述了数字化系统中雷达杂波生成的理论原理和计算方法，为雷达数字化设计与仿真系统杂波模拟提供了理论参考和方法依据，并可借鉴于雷达杂波的设计与实现工作。