桥头路堤-桥台-地基作用体系的地震反应分析

程志明，魏红卫

桥头路堤-桥台-地基作用体系的地震反应分析

程志明1, 2，魏红卫1

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 武汉市政工程设计研究院有限责任公司，湖北 武汉 430023)

考虑桥头路堤、桥台、地基相互作用，建立路桥过渡段三维动力分析模型，输入汶川地震波，进行非线性地震反应时程分析。将数值计算结果，与经典理论和规范方法计算结果、离心试验结果，以及震害调查资料对比分析，证实计算模型和计算方法的合理性。着重计算桥头路堤、桥台、地基的地震位移反应，桥台的地震加速度、土压力、弯矩以及基底剪应力反应等。计算结果表明：震后桥台整体背离路堤滑移，并伴随下沉和外倾，地震位移包含平移与转动2部分，桥台顶部加速度存在放大效应，承受的地震土压力以及弯矩内力较震前明显增大，相比而言，公路规范与铁路规范方法的计算值偏小；震后桥头路堤向桥台方向推移，存在拉裂趋势和不均匀沉降破坏；地基与桥台基础相邻部位，峰值水平位移与残余水平位移以及最终沉降量相对较大，基底剪力大幅增加，桥台与地基出现相对滑移。研究结果对桥梁抗震加固设计具有借鉴意义。

桥头路堤；桥台；地基；地震反应；时程分析

我国地处世界两大地震带之间，是一个多地震国家，四千二百余年的地震文献记载表明，除浙江、江西两省外，我国绝大部分地区都发生过震级较大的破坏性地震[1]。近年来的公路桥梁地震灾害调查表明，公路路基与桥梁衔接部位的地震破坏非常多见，是地震中的薄弱环节[2−5]。由于地震引起的桥头路堤坍滑、沉陷，侧向位移，桥台地基不均匀沉降等，通常会引发桥梁结构地震动放大，从而加剧结构的地震破坏。因此，研究桥头路堤、桥台、地基的地震反应及其相互作用特性，对公路桥梁的抗震加固设计很有实际意义。国内不少外学者都很重视相关方面的研究，分别采用不同方法，从不同侧重面进行了富有成效的工作，得到了很多有益结论。为了研究桥台振动对桥梁结构的影响，LI等[6]采用单跨梁桥模型，沿桥梁纵向激振进行振动台试验，研究桥台固定方式对桥梁冲击的影响。Anne等[7]选用美国加州典型的台背回填材料粉砂进行横向循环加载试验，研究桥台可牺牲背墙的土压力特性，认为背墙位移为0.03(墙高)时，土压力达到最大值，相应被动土压力系数为16.3；在深度处有一个对数螺旋主破坏面，被动楔块中还有几个相对较小的剪切面，可假定对数螺旋滑移破裂面，采用条分法估算土压力；墙−土界面摩擦作用约为土体摩擦角的1/3到1/2。何度心[8]通过振动台试验研究桥头路堤和桥台的地震响应，发现路堤中孔隙水压力增大，桥台与台后土体滑移，台后填土裂缝，路面塌落，台身滑移、倾斜、沉陷等。王建等[9]选取现场路堤填料，采用长3.5 m、宽1.5 m、高2 m的模型箱，输入人工合成波进行试验，结果表明路堤呈现上部拉裂、下部鼓胀的破坏性状，印证了震害调查结果。为了估算桥台的位移，苏谦等[10]通过简化桥台滑动破坏模式，考虑土体强度衰减效应对桥台稳定性的影响，提出了桥台滑移计算公式。唐红梅等[11]利用毕肖普法计算桥台的地震位移，结合工程实例验证方法的可靠性，并分析了黏聚力、振动孔隙水压力和内摩擦角等因素对位移的影响。Anoosh等[12]采用对数螺旋破坏面耦合修正的双曲线土体应力−应变模型，用极限平衡法估算桥台非线性位移，根据8个典型结构回填土的现场试验结果，验证了计算方法的适应性，并利用最小二乘法和试验数据，建立简化的双曲线力−位移方程，认为其计算结果用于桥台抗震设计符合现有加州交通部门的要求。Al-Homoud等[13]进行了桥台和填土非线性地震反应分析，并考虑桥台转动和滑移条件，提出桥台抗震设计方法，但计算分析中没有考虑梁对桥台的作用，并将其视为平面问题。孙治国等[14]利用ANSAYS建立了高原大桥三维有限元模型，研究桥台破坏机理，并对抗震措施进行分析，认为胸墙、前墙以及其与翼墙交界处是地震中薄弱部位。这些研究从不同侧面丰富和完善了关于桥头路堤、桥台、地基相互作用特性的内涵，很有实际意义。由于桥头段地震特性不但决定于桥台、路堤、地基和锥坡自身振动特性，还与其相互作用特性密切相关，地震反应计算涉及到不同材料和不同结构形式的组合，以及桥台与路堤、地基以及锥坡的多重界面处理，考虑因素多，计算分析难度大，耗时长，有诸多方面还需进一步研究。本文基于FLAC3D计算平台，考虑桥台、路堤、地基和锥坡的相互作用，建立三维动力计算分析模型，研究桥台−路堤−地基作用体系的地震反应规律，旨在为相应的抗震设计加固提供一定的理论借鉴。

1 计算方法

1.1 计算模型

实际桥台−路堤−地基作用体系包括桥台、梁、地基、路堤与锥坡五部分，为了简化计算，本文假定梁对桥台仅传递竖向荷载，将梁与桥台的作用简化成竖向力，模型仅包括桥台、地基、桥头路堤和锥坡。

几何模型见图1，其中路堤宽12 m，高6 m，路堤两侧边坡坡度1:2。埋置式桥台高8 m、厚2 m、宽12 m，扩大基础埋深2 m，厚4 m，宽12 m。桥台左右两侧与前侧设置锥坡，坡度1:2，尺寸设置与公路工程技术标准典型断面尺寸一致。考虑到模型边界对计算精度的影响，经试算，计算幅度确定为地基长80 m，宽48 m，厚20 m。为了波在网格中的合理传播，网格单元尺寸均小于最小波长的1/10，邻近桥台的路堤和地基土体网格加密[1, 15-19]，网格划分见图2。

图1 桥台-路堤-地基作用体系示意

图2 计算模型

1.2 材料参数

相对土体，桥台的刚度与强度大得多，为简化计算，忽略桥台的塑性变形，视为线弹性结构，土体为摩尔−库伦材料，参数见表1。

1.3 接触面处理

桥台与地基、路堤以及锥坡的材料和结构特性相差较大，其间存在滑移、分离，本文通过在桥台与土体之间设置接触面单元来考虑土−结构界面作用，当两侧的模量差异较大时，接触面的法向刚度与切向刚度可取“较软”材料等效刚度的10倍，按式1计算，由于接触面有交叉，需要对其参数进行折减，接触面摩擦角一般要小于填土的内摩擦角，本模型取为10°，接触面的具体参数见表2[16, 19]。

表1 模型材料参数

表2 接触面参数

1.4 边界条件与阻尼设置

静力计算时，底部采用固定边界，四周采用滑移支座约束水平位移，动力计算时，考虑波的反射，底部采用黏滞边界，四周采用自由场边界。

阻尼通常可采用瑞利阻尼、滞后阻尼与局部阻尼等，Manica等[20]对比分析了3种阻尼的计算效果，表明瑞利阻尼得出的结果与实际的最吻合，因此本文采用瑞利阻尼。岩土工程中，土体达到塑性变形后会消耗一部分能量，因此阻尼比可取较小值，一般为2%~5%，本文取2%。

1.5 地震荷载输入

研究时分别选取了Kobe波、Loma Prieta波、汶川波作为输入波，为节约篇幅本文仅以汶川波为例，其他相应分析详见文献[21]。

由于三维动力分析模型计算耗时太长，为提高计算效率，选取汶川地震中卧龙台站所记录的东西向水平地震波，截取其中一个含波峰的，持时20 s的波段作为输入波，并进行基线校正处理，以便线弹性结构在动力计算结束后速度与位移为0[19]。处理后的汶川地震加速度时程与积分得到的位移时程见图3。

1.6 监测点布置

监测点布置见图4，从桥台顶部向下每隔1 m布置1个监测点，直至基础底部，扩大基础4个角另外各设1个监测点，为阐述方便，将桥台底部4个角编号为A，B，C和D。沿路线走向，远离桥台每1 m布置上、中、下3个监控点，至距桥台10 m处，每2 m布置监测点，至距桥台20 m处。基础中心正下方的地基中，向下每2 m布置1个监 测点。

1.7 计算过程

计算分为静力计算与动力计算两部分。先进行静力计算，采用小变形模式进行静力平衡，在施加梁对桥台的竖向力时，为了避免产生过大的应力集中，分5步进行加载。然后开启大变形模式进行动力计算，将静力计算后的位移场、速度场清零，保留应力场，在模型底部施加水平方向地震荷载，采用动态时步模式。

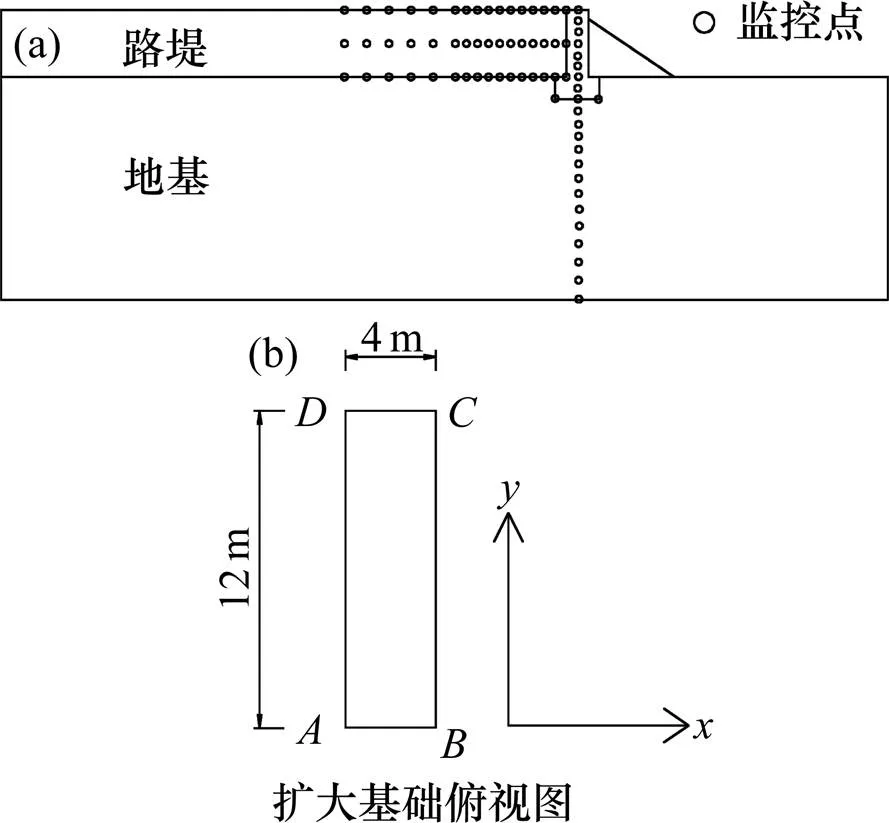
图4 监测点布置示意

2 计算结果分析

2.1 静力反应

静力平衡后，模型竖向应力云图见图5，由图可见，模型竖向应力呈现明显分层现象，随深度增加竖向应力逐渐增大，底部达到426.77 kPa。

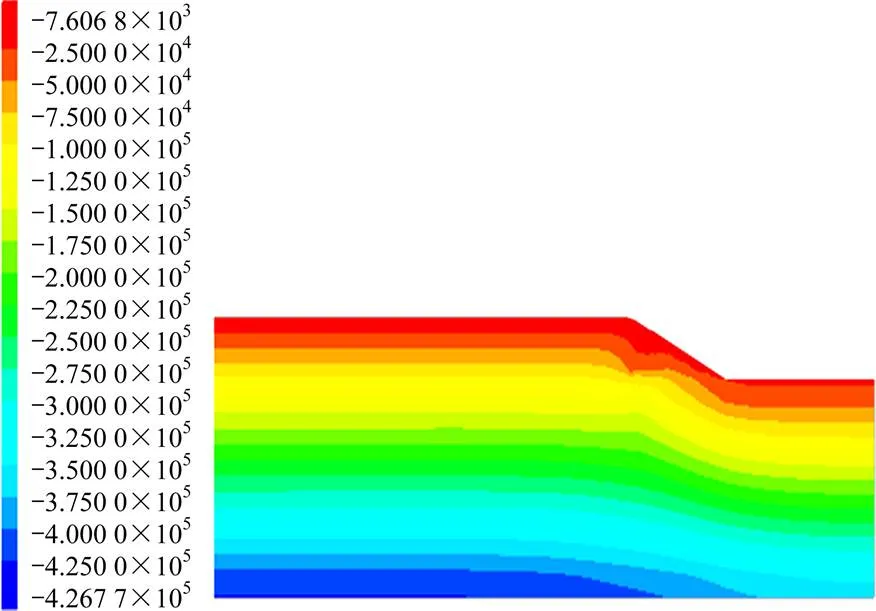
图5 静力计算竖向应力云图

路堤对桥台的土压力分布见图6，随着深度增加，路堤土压力非线性增大，呈内凹抛物线形分布，路堤总土压力165.313 kN。根据朗肯理论计算，路堤主动土压力95.836 kN，被动土压力876.266 kN，本文方法计算的静止土压力介于朗肯主动土压力和被动土压力之间。由于静力平衡时，桥台顶部位移为−0.624 mm，向路堤侧偏移，推动回填土，因此，计算土压力大于主动土压力[16]。同时，从路堤土压力分布看，其内凹抛物线形与Springman等[22]的离心机试验结果得到的分布规律吻合，由此说明本文计算模型和计算方法是合理的。

图6 震前土压力分布

桥台基础中心下方地基沉降沿深度变化见图7，靠近桥台底部的地基沉降较大，深处沉降相对较小。本文计算方法所得沉降与按《建筑地基基础设计规范》(GB 50007—2011)[23]计算沉降的大小接近，最大差值仅为2.022 mm，沿深度的变化趋势基本一致，都呈外凹抛物线形，进一步验证了本文计算模型和计算方法的合理性。

2.2 桥台地震反应

输入汶川波计算，桥台顶部水平位移时程见图8。

为节约篇幅，桥台其余各监测点的位移时程参见文献[21]。由图可见，桥台顶部位移呈波动变化，位移动力响应很明显，在第14.922 74 s时达到峰值位移312.526 mm后，随着地震波主能量段的过去，桥台发生部分回弹，出现67.762 mm的残余水平位移。由于桥台为线弹性，残余水平位移主要由周围弹塑性土体引起。赖杰等[24]采用汶川波激振，利用振动台试验研究抗滑桩的抗震性能，本文计算得到的桥台位移时程曲线与其试验监测到的抗滑桩位移时程曲线特征类似。

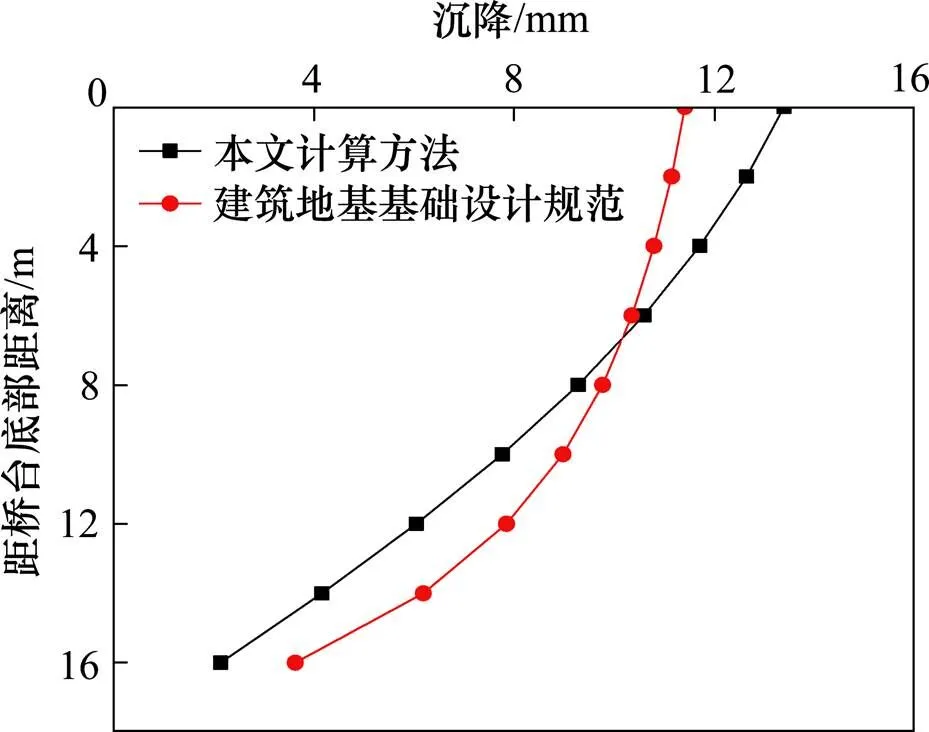
图7 地基沉降

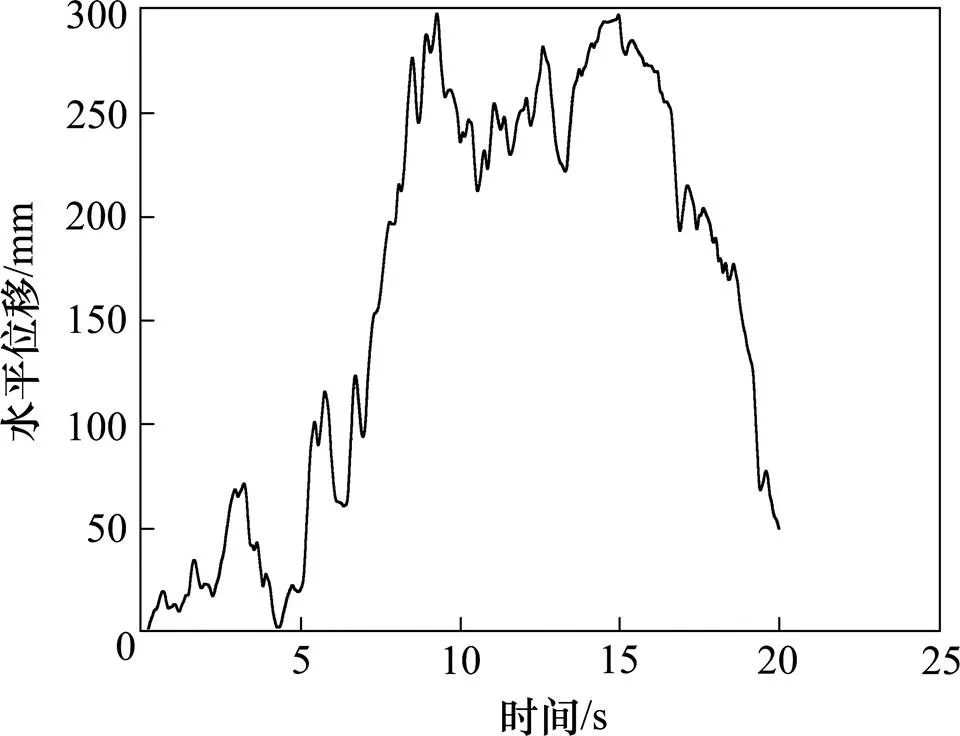
图8 桥台顶部水平位移时程

桥台各监测点峰值水平位移与残余水平位移见图9，桥台残余水平位移均为正值，表明桥台震后整体向远离路堤方向移动。同时，无论桥台的峰值水平位移还是残余位移，顶部与底部均不相同，说明桥台发生了倾斜，表明地震过程中桥台位移包含平移与转动2种成分。桥台残余位移斜线与竖轴的夹角大于峰值位移斜线的夹角，说明地震结束时桥台的倾斜角度大于峰值时刻，桥台倾斜角度随着震动持时而累积。

桥台扩大基础底部4个角的竖向位移时程见图10，A点与D点，B点与C点的竖向位移时程曲线基本一致，这是由于它们分别关于道路中线对称的原因。桥台沉降整体呈波动增大趋势，A点在18.236 s时达到最大值14.957 mm，地震结束时沉降为14.604 mm，B点在17.328 s时达到最大值20.153 mm，最终沉降为19.493 mm，A，B相差4.889 mm，说明桥台发生旋转，B点最终沉降大于A点，表明桥台向外倾斜，不均匀沉降随着地震持时而增大，即倾斜角度随时间逐渐增大。

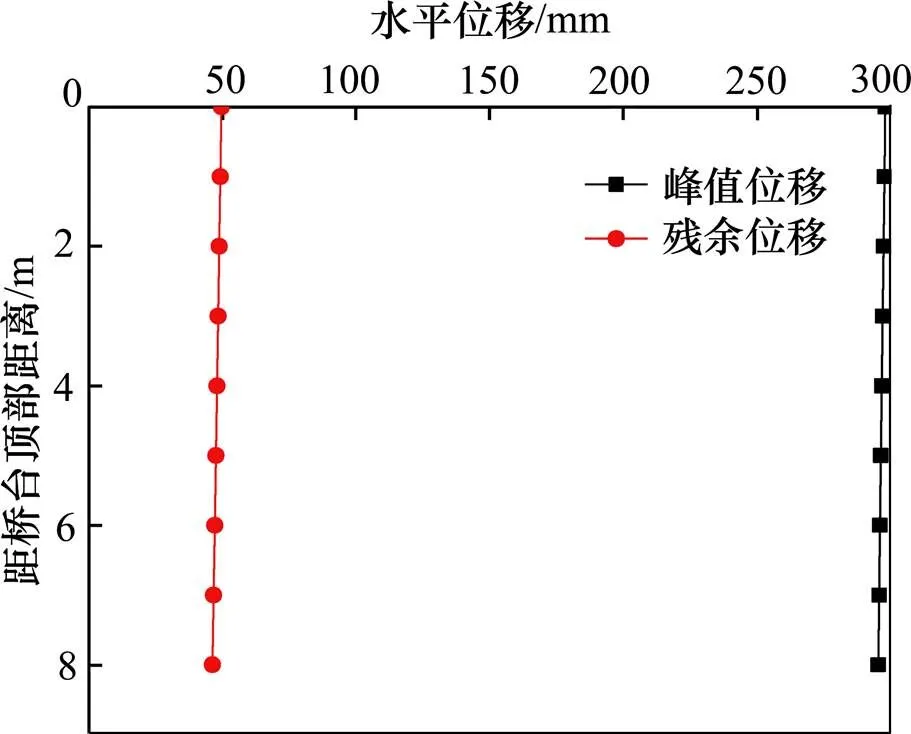
图9 桥台峰值水平位移与残余水平位移

图10 桥台竖向位移时程

桥台峰值加速度分布见图11，由图11可见，桥台峰值加速度与加速度放大系数沿桥台高度整体呈增大趋势，桥台底部的峰值加速度大于距桥台顶部5~7 m处的峰值加速度，这是因为该处是桥台与地基交界面，受地震作用较强，故对应峰值加速度较大。峰值加速度增大幅度随着高度的增大而增大，由底部的5.948 m/s2增加至顶部的10.520 m/s2，整体上，加速度沿桥台竖向上存在放大效应，而且刚开始增大缓慢，到达一定高度时，峰值加速度急剧增大，加速度放大系数达到2.630。

图11 桥台加速度峰值

路堤土压力沿桥台高度变化见图12，由图可见，地震土压力最大值出现在距桥台顶部4.5 m处；本文计算的路堤地震峰值土压力与物部-冈部法(M-O法)以及规范方法的计算结果对比见表3，路堤地震峰值土压力为353.588 kN，M-O法计算值为363.573 kN，公路规范为295.262 kN，铁路规范为268.239 kN，本文计算路堤峰值土压力大于公路规范与铁路规范，与M-O法计算结果接近。

图12 土压力分布

表3 地震土压力

2.3 桥头路堤地震反应

与台背相邻处路堤表面的水平位移时程见图13，其余各点的位移时程曲线可参见文献[21]。由图可见，水平位移最大值为312.485 mm，残余位移为67.727 mm；相同高度处桥台的峰值水平位移为312.526 mm，残余水平位移为67.762 mm，桥台与路堤相邻处位移不同，存在分离现象，这与震后现场桥头路堤与桥台常出现裂缝现象相吻合。

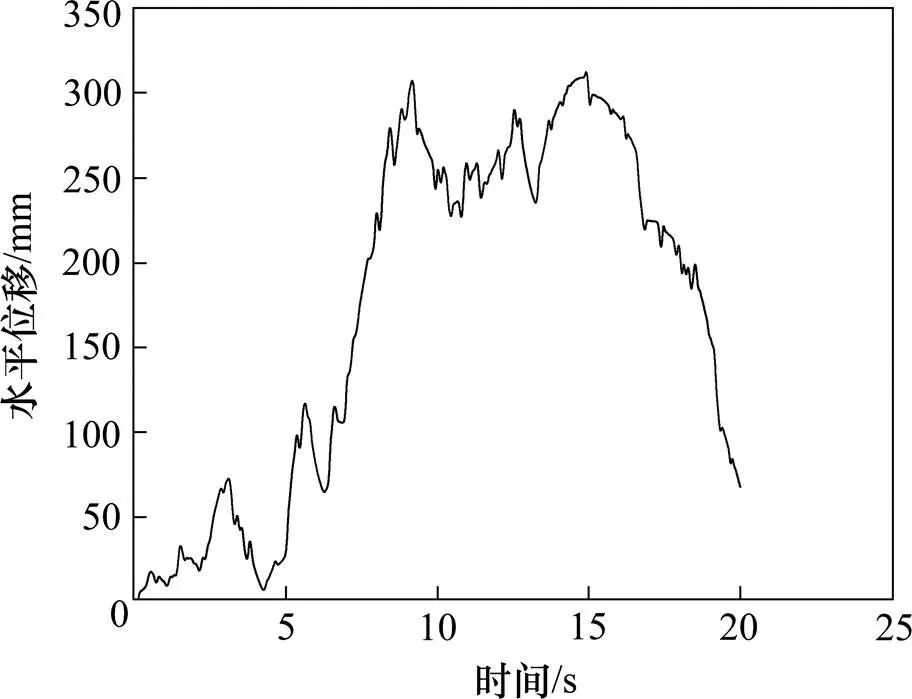
图13 台背相邻处路堤表面水平位移时程

路堤表面各监测点峰值水平位移与残余水平位移见图14，由图14可见，距台背0，5，10和20 m处路堤表面峰值水平位移分别为312.495，306.691，305.321和303.625 mm，残余水平位移分别为67.727，60.404，58.787和56.948 mm，路堤表面的峰值水平位移与残余水平位移随远离台背而减小，可见路堤有拉裂趋势。

距台背0，5和10 m处路堤表面的竖向位移时程曲线见图15，由图15可见，随地震作用持续，各点竖向位移逐渐增大，但距台背0，10和20 m处各点竖向位移不同。

路堤表面最终沉降见图16，由图16可见，最终沉降随着距台背距离的增加呈减小趋势。从路堤的水平位移与竖向位移可发现，路堤有拉裂的趋势，桥头段路堤变形较大，呈塌滑趋势，是地震中的薄弱点，而且桥头路堤已经与桥台发生分离，这些变形和破坏特征与震后调查结果一致[2−4]。

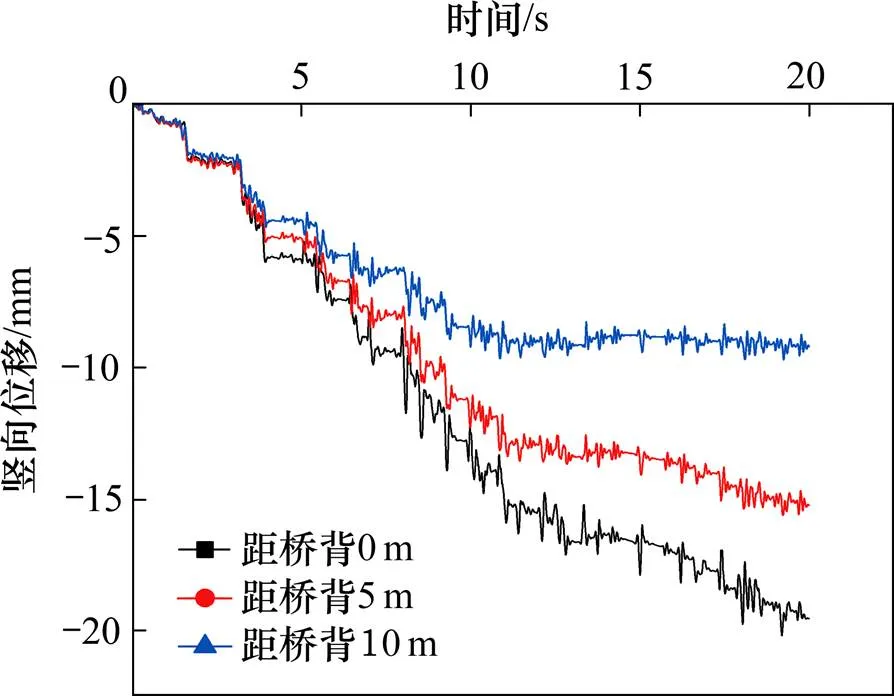
图15 路堤表面竖向位移时程

图16 路堤表面最终沉降

2.4 地基地震反应

与桥台底部相邻处地基的水平位移时程见图17，水平位移在14.899 59 s达到峰值307.279 mm，残余水平位移为59.472 mm，而桥台底部峰值水平位移为307.186 mm，残余水平位移为60.132 mm，可见，在地震过程中，桥台底部与地基产生相对滑移。地基峰值水平位移与残余水平位移见图18，地基峰值水平位移与残余水平位移随着深度的增加而减小，地基底部残余水平位移为43.247 mm，为顶部的72.718%。

图17 桥台相邻处地基土水平位移时程

图18 地基峰值水平位移与残余水平位移

距桥台底部0，10和18 m处的地基竖向位移时程见图19，距桥台底部0 m处峰值竖向位移−17.216 mm，残余位移−16.976 mm；距桥台底部10 m处峰值竖向位移−8.189 mm，残余位移−7.689 mm；距桥台底部18 m处峰值竖向位移为−1.592 mm，残余位移为−1.068 mm。

图19 地基竖向位移时程

图20 基底剪力时程

基底剪力时程见图20，基底剪力在地震中呈波动增加趋势，在第8.678 s达到最大值295.046 kN，相对震前剪力59.505 kN，增大幅度达206.6%，地震结束时的残余剪力为106.174 kN。从前文已知存在相对滑移，抗震设计时应进行抗滑移验算。

3 结论

1) 本文计算台背土压力处于朗肯主动土压力与被动土压力之间，分布特征与离心机试验结果相吻合；计算的地基沉降与规范方法计算结果接近，变化趋势一致；计算的地震峰值土压力与M-O法计算结果接近；计算得到的路堤和桥台地震反应特征和破坏趋势与震后调查资料吻合良好，说明本文数值分析模型和计算方法较合理。

2) 震后桥台整体远离路堤滑动，并呈整体下沉和外倾状态，地震位移包含平移与转动；桥台加速度在高度方向上存在放大效应，承受的地震峰值土压力与最大弯矩较震前明显增加，公路规范与铁路规范计算值偏小。

3) 路堤震后整体向桥台方向推移，路堤表面峰值以及残余水平和竖向位移反应特征表明，桥头路堤在地震中易发生拉裂和不均匀沉降破坏，反映了桥头段的主要地震破坏特征。

4) 毗邻桥台的地基土体的峰值水平位移与残余水平位移以及最终沉降随较大；地震过程中基底剪力较震前有较大幅度增加，存在相对滑移。

[1] 陈国兴. 岩土地震工程学[M]. 北京: 科学出版社, 2007. CHEN Guoxing. Geotechnical and seismic engineering [M]. Beijing: Science Press, 2007.

[2] 王东升, 郭迅, 孙治国, 等. 汶川大地震公路桥梁震害初步调查[J]. 地震工程与工程振动, 2009, 29(3): 84−94. WANG Dongsheng, GUO Xun, SUN Zhiguo, et al. Damage to highway bridges during Wenchuan earth -quake[J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(3): 84−94.

[3] 庄卫林, 陈乐生. 汶川地震公路震害分析(桥梁与隧道) [M]. 北京: 人民交通出版社, 2013. ZHUANG Weilin, CHEN Lesheng. Analysis of highway earthquake damage in Wenchuan earthquake (Bridges and tunnels)[M]. Beijing: Communication Press, 2013.

[4] 杜修力, 韩强, 李忠献, 等. 汶川地震中山区公路桥梁震害及启示[J]. 北京工业大学学报, 2008, 34(12): 1270−1279. DU Xiuli, HAN Qiang, LI Zhongxian, et al. Earthquake damage of highway bridges in mountainous areas and its enlightenment in 512 Wenchuan earthquake[J]. Journal of Beijing University of Technology, 2008, 34(12): 1270− 1279.

[5] 庄卫林, 陈乐生. 汶川地震公路震害分析(地质灾害与路基)[M]. 北京: 人民交通出版社, 2013. ZHUANG Weilin, CHEN Lesheng. Analysis of highway earthquake damage in Wenchuan earthquake (Geological hazards and roadbed)[M]. Beijing: Communication Press, 2013.

[6] LI B, BI K, Chouw N, et al. Effect of abutment excitation on bridge pounding[J]. Engineering Structures, 2013, 54(3): 57−68.

[7] Anne Lemnitzer S, Eric R, Ahlberg A, et al. Lateral performance of full-scale bridge abutment wall with granular backfill[J]. J Geotech Geoenviron Eng, 2009, 135(4): 506−514.

[8] 何度心. 桥台抗震设计的理论与方法[J]. 世界地震工程, 1991, 50(3): 1−15. HE Duxin. Theory and method of seismic design of bridge abutment[J]. World Earthquake Engineering, 1991, 50(3): 1−15.

[9] 王建, 姚令侃, 吴伟. 路堤震害模式及路堤动力特性研究[J]. 岩土力学, 2010, 31(12): 3801−3808. WANG Jian, YAO Lingkan, WU Wei. Research on seismic damage mode and dynamic characteristics of road embankment[J]. Rock and Soil Mechanics, 2010, 31(12): 3801−3808.

[10] 苏谦, 钟彪, 白皓, 等. 基于滑坡破坏模式的桥台位移耦合计算[J]. 土木工程学报, 2010, 43(增1): 567−572. SU Qian, ZHONG Biao, BAI Hao, et al. Coupled calculation of abutment displacement based on landslide failure mode[J]. China Civil Engineering Journal, 2010, 43(Suppl 1): 567−572.

[11] 唐红梅, 刘荣灿, 陈洪凯. 地震作用下桥台滑移计算方法及应用[J]. 公路, 2010, 20(3): 42−47. TANG Hongmei, LIU Rongcan, CHEN Hongkai. Calculation method and application of bridge abutment slip under earthquake action[J]. Highway, 2010, 20(3): 42−47.

[12] Anoosh Shamsabadi, Kyle M Rollins, Mike kapuskar. Nonlinear soil-abutment–bridge structure interaction for seismic performance-based design[J]. J Geotech Geoenviron Eng, 2007, 133(6): 707−720.

[13] Al-Homoud A, Whitman R. Seismic analysis and design of rigid bridge abutments considering rotation and sliding incorporating non-linear soil behavior[J]. Soil Dynamics and Earthquake Engineering, 1999, 18(4): 247−277.

[14] 孙治国, 王东升, 张蓓, 等. 高原大桥桥台地震破坏机理与抗震措施分析[J]. 地震工程与工程振动, 2012, 32(4): 79−87. SUN Zhiguo, WANG Dongsheng, ZHANG Bei, et al. Analysis of seismic failure mechanism and earthquake resistant measures for the abutments of Gaoyuan[J]. Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(4): 79−87.

[15] 祁生文, 伍法权,严福章, 等. 岩质边坡土动力反应分析[M]. 北京: 科学出版社, 2007. QI Shengwen, WU Faquan,YAN Fuzhang, et al. Rock slope dynamic response analysis[M]. Beijing: Science Press, 2007.

[16] 钱家欢, 殷宗泽. 土工原理与计算[M]. 北京: 中国水利水电出版社, 1996. QIAN Jiahuan, YIN Zongze. Geotechnical principles and computation[M]. Beijing: China Water Resources and Hydropower Press, 1996.

[17] 吴世明. 土动力学[M]. 北京: 中国建筑工业出版社, 2000. WU Shiming. Soil dynamics[M]. Beijing: China Construction Industry Press, 2000.

[18] Francisco M, Fernando R. Spurious reflections and accuracy of finite element models for unbounded wave propagation problems: the one-dimensional case[J]. Engineering Computations, 1987, 4(2):139−148.

[19] 陈育民, 徐鼎平. FLAC/FLAC3D基础与工程实例[M]. 北京: 中国水利水电出版社, 2013.

CHEN Yumin, XU Dingping. FLAC/FLAC3Dfoundation and engineering example[M]. Beijing: China Water Resources and Hydropower Press, 2013

[20] Manica M, Ovando E. Assessment of damping models in FLAC[J]. Computers & Geotechnics, 2014, 59(6): 12−20.

[21] 程志明. 桥台−路堤−地基作用体系的地震反应分析[D]. 长沙: 中南大学, 2019. CHENG Zhiming. Analysis of abutment-embankment- foundation interaction system subjected to seismic load [D]. Changsha: Central South University, 2019.

[22] Springman S, Ng C, Ellis E. Centrifuge and analytical studies of full height bridge abutment on piled foundation subjected to lateral loading[R]. CUED/D-SOILS/TR278. 1994: 1−120.

[23] GB50007—2011, 建筑地基基础设计规范[S]. GB50007—2011, Code for design of building foundation [S].

[24] 赖杰, 郑颖人, 刘云, 等. 地震作用下双排抗滑桩支护边坡振动台试验研究[J]. 岩土工程学报, 2014, 36(4): 680−687. LAI Jie, ZHENG Yingren, LIU Yun, et al. Shaking table tests on double-row anti-slide piles of slopes under earthquakes[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 680−687.

Analysis of abutment-embankment-foundation interaction system subjected to seismic load

CHENG Zhiming1, 2, WEI Hongwei1

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. Wuhan Municipal Engineering Design and Research Institute Co., Ltd., Wuhan 430023, China)

A three-dimensional non-linear numerical model of approach embankment was established considering abutment- embankment-foundation interaction, and the Wenchuan earthquake wave was used as seismic load to carry out the non-linear time history analyses of seismic response. Comparing the results of numerical calculation with those of classical theory and standard method, centrifugal test results and seismic damage investigation data, the rationality of the calculation model and method was verified. The main analyses included the seismic displacement responses of embankment, abutment and foundation, seismic accelerations, earth pressure, bending moments and base shear stress response of abutment. The results show that the abutment deviated from the embankment, accompanied with sinking and extroversion after earthquake, and the seismic displacements included translation and rotation. The acceleration at the top of the abutment appeared amplification effect, and the seismic earth pressure and bending moments were obviously increased compared with those before earthquake. Comparatively, the calculation results by highway code and railway code method appeared to be smaller. After earthquake, the main seismic damage behaviors in approach embankment were crack and differential settlement; The peak and residual horizontal displacement, and final settlement of foundation soil adjacent to abutment were relatively large, and the shear force between the foundation and abutment increased greatly in earthquake which led to a relative slip. The results in this paper will be beneficial to seismic reinforcement design of bridges.

embankment; abutment; foundation; seismic response; time history analysis

TU416.1

A

1672 − 7029(2020)09 − 2225 − 10

10.19713/j.cnki.43−1423/u. T20191094

2019−12−06

国家自然科学基金面上项目(51778639，51678573)

魏红卫(1966−)，男，河南汝州人，教授，博士，从事结构工程与岩土工程的教学和研究工作；E−mail：whw.edu@163.com

(编辑 涂鹏)