基于改进粒子群算法和神经网络的智能位移反分析法及其应用
2020-10-15凌同华秦健宋强华斐
凌同华,秦健,宋强,华斐
基于改进粒子群算法和神经网络的智能位移反分析法及其应用
凌同华,秦健,宋强,华斐
(长沙理工大学 土木与建筑学院,湖南 长沙 410114)
为确定工程计算所需的围岩力学参数,提出一种基于改进粒子群算法和BP神经网络的智能位移反分析方法,结合工程现场量测到的围岩位移信息,实现对隧道围岩力学参数的反演。该方法利用正交和均匀试验设计方法获得训练样本,在动态改变惯性权重的同时加入粒子位置自适应变异,对标准粒子群算法进行改进,并利用改进算法对BP神经网络权值和阈值进行优化,提高网络训练速度和预测精度;再利用该神经网络建立起待反演参数与实测位移值间的非线性关系,结合改进粒子群算法搜索最优反演参数。将此方法应用于里岩垄隧道YK11+150断面反分析中,比较计算位移值和实测位移值,其平均相对误差为5.35%,表明该方法是可行的。
隧道工程;位移反分析;粒子群优化算法;BP神经网络
准确地确定岩体力学模型及其模型参数是进行岩土工程设计及应用的关键。因此人们依据工程现场量测的位移信息反演确定有关力学参数,提出了位移反分析法。目前位移反分析法常采用的计算方法为优化反分析法[1],其实质就是通过迭代计算寻找一组待反演参数使计算位移值与实测位移值误差最小,但该类算法在迭代过程中将进行多次有限元等数值方法的计算,是一种非常耗时的算 法[2−4]。针对这一不足,冯夏庭等[5]提出利用神经网络预测围岩变形值来代替有限元计算,并结合遗传算法的优化能力,提出了一种进化神经网络的位移反分析方法;之后,周冠南等[6]将进化神经网络方法成功应用于大顶山隧道围岩力学参数的位移反分析中;谷淡平等[7]考虑参数不确定性条件下,用响应面法建立了岩体强度参数与安全系数的关系式,对边坡滑面强度参数进行了反演分析;GUO 等[8]则采用响应面法代替有限元分析,提出了一种基于响应面法和遗传算法的反分析方法;但基于遗传优化算法存在程序繁琐,收敛速度慢的不足,此时,高玮[9]开始采用一种优化效率更高的粒子群算法进行反分析研究;孙斌等[10−11]则将粒子群算法与数值方法结合对隧道岩体力学参数进行了反演分析;吴忠广等[12−13]通过使用粒子群算法优化多输出支持向量机,实现了对多围岩参数的概率反演;阮永芬等[14]采用小波理论和粒子群算法优化支持向量机模型参数进行岩土力学参数反演,并对地基的最终沉降量进行了预测;同时,刘忠豹等[15−16]编制了PSO-BP的混合算法程序对大坝变形及边坡稳定性进行了预测。由此可见神经网络结合粒子群优化算法的混合算法已广泛应用于岩土工程,但神经网络收敛速度和预测精度易受初始权值和阈值的影响。此外,PSO算法也存在早熟收敛,不能保证搜索到全局最优解的问题。本文就惯性权重的自适应调整和粒子位置的自适应变异对粒子群算法进行综合改进,并利用改进算法优化BP网络,同时采用正交试验设计和均匀试验设计方法确定样本试验方案,利用Midas/GTS有限元软件模拟实际地形及地层情况建立三维模型,获得BP网络的学习和测试样本,再利用监控量测得到的围岩位移信息,结合神经网络的仿真预测功能和粒子群算法寻优能力搜索最优反演参数,并通过在里岩垄隧道中应用该方法验证其有效性。
1 基本原理
1.1 BP神经网络
BP神经网络[17]是一种前馈型分层神经网络,它可以实现从输入到输出的任意非线性映射。BP网络由一个输入层、一个输出层和一至多个隐含层组成,每层包含若干节点,节点之间通过权值阈值进行连接,其学习过程由输入信息的前向传播和误差的反向传播两个过程组成。对于输入信号,在相应连接权值和阈值及传递函数的作用下从输入层经隐含层逐层处理,传向输出层。在输出层不能达到理想的结果时,误差反向传播,通过调整各层神经网络的权值和阈值,使BP神经网络预测输出不断逼近期望输出。

图1 算法搜索示意图
1.2 粒子群优化算法
粒子群优化算法[18]结构简单,需要调整的参数少,目前已应用于多个科学和工程领域。算法在求解优化问题时,首先在可行解空间中初始化一群粒子,每个粒子都为优化问题的一个潜在最优解,再通过目标函数计算粒子的适应度值来表示粒子的优劣,最后经迭代找到最优解。在每一次迭代中,粒子通过跟踪2个“极值”来更新自己:一个是粒子本身找到的最优解,即个体极值点;另一个是整个群体目前找到的最优解,称为全局极值点,其速度和位置更新公式如下:



2 改进的粒子群优化算法
同其他全局优化算法一样,粒子群算法也存在早熟收敛现象。针对这一情况,提出了一种动态改变惯性权重并结合粒子自适应变异的改进粒子群算法。
2.1 惯性权重的自适应调节
根据算法运行状态进行惯性权重的调整,可以更好地平衡算法进行全局搜索和局部搜索的能 力[19]。
在粒子群算法迭代过程中,当前迭代的全局最优适应度值(T)总是优于前次迭代的全局最优适应度值(T−1)。因此定义邻近2次迭代过程的全局最优适应度比值为粒子群进化速度。

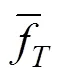


如果粒子群进化速度较快时,可取较大的值,让粒子保持大范围寻优能力,当进化速度减慢时,则可以减小值,使得粒子群在最优解附近进行精细搜索;如果粒子聚集程度小,粒子群就不易陷入局部最优解,但随着迭代次数的增加会出现粒子聚集的现象,此时应增大值,扩大粒子群的搜索范围,避免算法陷入局部最优。因此,惯性权重应随着粒子聚集度的增大而增大,随着进化速度的减小而减小,可表示为和的函数,即

式中:ω为惯性权重初始值;一般取1,ω在0.4~0.6范围内取值;ω在0.05~0.2范围内取值。
2.2 粒子的自适应变异
若算法能判断出粒子群已陷入局部最优解,并采取措施增加粒子多样性,使粒子跳出先前搜索到的最优位置,继续进行搜索就能避免算法出现早熟收敛[20]。
为了能够准确判断算法是否已陷入局部最优解,采用粒子群适应度方差2对粒子群的聚集程度进行定量描述:



通过考察粒子群适应度方差、粒子适应度值同个体最优适应度值的关系以及当前全局最优适应度值来确定变异时机,当式子(9)成立时,则发生 变异。


当粒子变异条件成立时,就判定算法陷入了局部最优解,并对符合条件的粒子按式(11)进行位置变异,让粒子跳出局部最优解,进行更大范围的进行搜索。


式中:[·]为取整函数;为解空间的维度;x()为第个粒子的第维取值;为粒子位置取值范围上下限之差,1和2为0~1间的随机数。
采用如式(12)Schaffer函数在[−5,5]范围内对标准PSO算法和改进PSO算法进行性能测试:

发现改进算法具有更强的寻优能力,能搜索到函数的全局极小值点(0,0,0)。
3 基于改进PSO算法和神经网络的智能位移反分析法
基于改进PSO算法和神经网络的智能位移反分析法的基本思路是:结合现场实测围岩位移信息,由正交和均匀试验设计方法确定试验方案,经有限元计算建立BP网络的学习和测试样本,再利用改进PSO算法优化BP网络,最后通过改进PSO算法搜索适应度函数的最优解,确定围岩力学参数值。
3.1 改进PSO算法优化神经网络
利用改进PSO算法对BP神经网络初始权值阈值进行优化,使初始参数更接近最优参数,并将优化得到的初始权阈值赋值给网络,继续进行PSO算法寻优,同时加入网络训练过程,建立最佳的BP神经网络模型。
改进PSO算法优化BP神经网络算法步骤 如下:
1) 构建BP神经网络,包括网络输入层、输出层、隐含层神经元个数和网络参数设置;
2) 设定PSO算法参数,如粒子维度、初始惯性权重、学习因子、粒子群规模和最大迭代次数,并初始化粒子群速度和位置;
3) 计算粒子的适应度值,选择预测数据和实测数据的均方方差MSE作为适应度函数,进行适应度比较,确定全局最优解和个体最优解;


4) 判断算法是否满足收敛精度要求或达到最大迭代次数,若满足条件,则执行步骤10),否则执行步骤5);
5) 粒子速度位置更新,根据式(1)~(2)更新粒子的速度和位置,重新计算粒子的适应度值,并由式(7)和式(8)计算粒子群适应度方差;
6) 粒子群的自适应变异,由式(9)判断粒子是否满足变异条件,若不符合条件,执行步骤7),否则,根据式(10)和式(11)对粒子位置进行变异,并执行步骤7);
7) 结合BP网络训练,用粒子位置对网络权值阈值进行赋值,经网络训练后,将优化的权值和阈值对粒子位置进行重新编码;
8) 计算粒子的适应度值,找出新的全局最优位置和个体最优位置;
9) 惯性权重的自适应调整,根据式(3)到式(5)计算当前代数的粒子聚集度和进化速度,并更新惯性权重,迭代次数加1,并转到步骤4);
10) 输出最优的网络权值和阈值,算法运行结束。算法流程如图3所示。
3.2 改进算法进行反分析的步骤
利用优化后建立的BP神经网络代替有限元计算,在给定参数取值范围基础上,再通过改进PSO算法对围岩参数进行搜索寻优,具体运行步骤 如下:
1) 确定待反演参数的取值范围;
2) 训练和测试样本构造,采用正交和均匀试验设计方法确定试验方案,再通过有限元模型计算,得到训练和测试样本;
3) 改进PSO算法优化BP神经网络,经PSO算法优化和对训练样本进行学习,再通过测试样本检验后,得到最佳的BP神经网络模型;
4) 改进PSO算法参数寻优,利用BP网络的仿真预测功能,在给定参数取值范围内,结合PSO算法搜索最优参数值。

图3 改进PSO算法优化神经网络流程

图4 改进算法进行位移反分析流程
4 工程应用实例
里岩垄隧道为浙江省永康至武义改扩建公路沿线的控制性工程,设计长度为262 m,最大开挖高度为11 m,最大开挖跨度为17 m,隧道出口段最小埋深约6 m,围岩以强风化凝灰岩为主,岩体破碎自稳能力差,属于V级围岩,此外在出口段出现明显的偏压现象,坡比为1:1.25。拟采用本文提出的智能位移反分析法对围岩弹性模量、泊松比、黏聚力和内摩擦角进行反演。
4.1 隧道计算模型
利用Midas/GTS有限元分析软件建立三维隧道模型进行正交和均匀试验,对桩号YK11+136-166段进行开挖支护模拟。模型计算范围如下:沿隧道轴线方向取30 m,选取研究断面YK11+150,模拟隧道实际地形及地层情况[21],左右边界取5倍洞径约为70 m,下边界取3倍洞径约为45 m。模型左右边界以及前后部边界均施加法向约束,底部边界完全约束,上部边界为自由边界,围岩按均质弹塑性材料考虑,选用 Mohr-Coulomb准则,采用实体 单元进行模拟,初期支护中的喷射混凝土采用板单元进行模拟,采用植入式桁架线单元模拟系统锚杆,以此建立隧道三维计算模型如图5所示。

图5 里岩垄隧道计算模型
并根据图6所示双侧壁导坑法对隧道开挖和支护过程进行模拟:先施作管棚超前支护,开挖左右双侧壁导坑1,并施作初期支护Ⅱ;待侧壁导坑超前10 m后,开挖拱部核心土3,施作初期支护Ⅳ;然后依次开挖上下半断面核心土5、6,施作仰拱初期支护Ⅶ;最后拆除临时支撑,并施作仰拱二次衬砌Ⅷ及拱部、侧墙二次衬砌Ⅸ,其中ABC为拱顶沉降观测点,DE和GF为水平位移观测点。

图6 双侧壁导坑法施工示意图
4.2 建立训练和测试样本
根据现场试验资料,确定隧道围岩力学参数取值范围分别为弹性模量:1.2~2.4 GPa,泊松比:0.3~0.46,黏聚力:0.1~0.3 MPa,内摩擦角:20°~40°。将4个待反演参数和隧道埋深划分为5个水平,并利用正交设计和均匀设计方法[22]确定试验方案,将每组试验的参数值输入隧道计算模型中进行开挖支护模拟,可得到1组如图6中各测点位移的计算结果,其变化曲线如图7所示。

图7 YK11+150断面计算位移变化曲线
将相应测点的位移计算结果作为输出值,从而可以获得用于神经网络训练和测试的35个样本,如表1所示,其中试验序号1-25按正交表L25(56)进行设计,得到25个神经网络训练样本,26-30号按均匀表U*10(108)进行设计,得到10个神经网络测试样本。
4.3 反分析计算
4.3.1 改进PSO算法优化BP网络
在本次反分析计算中,输入参数和输出参数均为5个,同时经试算确定最佳隐含层节点数为15个,则确定BP神经网络结构为5-15-5。设定PSO算法的初始参数:粒子群规模=30,最大迭代次数=1 000,学习因子1=2=1.496 2,惯性权重随算法运行态势动态变化,取初始惯性权重ω=0.729 8,惯性权重调整参数ω=0.6,ω=0.05,粒子最大(小)速度max=−min=1。
基于Matlab神经网络工具箱编写改进PSO算法优化BP神经网络程序,将初次优化得到的权阈值赋值给网络,再加入网络训练,继续进行PSO算法搜索,经2次PSO算法优化后,网络全局误差为0.018 1,得到预测效果最佳的BP神经网络。优化后BP网络输出结果与数值计算结果对比如图8所示,改进PSO算法优化BP网络误差和适应度方差曲线如图9所示。

表1 神经网络训练和测试样本

图8 网络输出结果与数值计算结果对比
4.3.2 参数反演结果
选取里岩垄隧道YK11+150断面量测的拱顶沉降和周边位移数据,利用双曲线函数对其进行回归分析,将推算位移最终值作为反分析计算输入数据,分析结果如图9所示。
再利用网络的模拟计算能力,结合改进PSO算法搜索一组围岩力学参数使适应度函数值最小,作为反分析的最优解,即围岩力学参数反分析结果。反分析计算输入数据及反分析结果如表2所示,BP网络预测位移与实测位移对比如图11所示,改进PSO算法进行搜索时的预测误差和适应度方差曲线如图12所示。

图9 BP网络误差和适应度方差进化曲线

表2 反分析计算输入数据及反分析结果

图10 YK11+150断面量测位移回归分析

图11 网络预测位移值与实测位移值对比

图12 改进粒子群算法预测误差与适应度方差进化曲线

表3 断面位移对比
将反分析得到的围岩参数输入计算模型进行隧道开挖支护过程的模拟,计算相应测点的位移值,计算结果如表3所示。比较位移反分析中神经网络预测位移值和现场实测位移值,可以看出隧道YK11+150断面位移最大相对误差为7.34%,最小为2.46%,同时预测位移与反分析得出参数的有限元计算位移也吻合较好。因此认为隧道位移反分析的结果是可信的。
5 结论
1) 引入粒子群进化速度和粒子聚集度对算法运行状态进行评判,使惯性权重发生自适应调整;同时加入粒子位置的自适应变异,增加了粒子群的多样性,避免算法陷入局部最优解,提高了算法的收敛速度和精度。
2) 将改进PSO算法和BP神经网络结合进行位移反分析。改善了BP神经网络训练速度慢、易陷入局部最优解的问题,又利用了神经网络的广泛映射能力和PSO算法的全局优化特性,从而能得到反演参数的最优解。
3) 结合隧道实测位移值,应用此方法进行隧道围岩位移反分析,将网络预测位移值、有限元计算位移值同实测位移值进行比较,其平均相对误差分别为5.35%和5.81%,计算精度满足要求,验证了该方法的有效性。
[1] 冯夏庭. 智能岩石力学导论[M]. 北京: 科学出版社, 2000: 71−72. FENG Xiating. An introduction to the intelligent rock mechanics[M]. Beijing: Science Press, 2000: 71−72.
[2] Kodama J, Miyamoto T, Kawasaki S, et al. Estimation of regional stress state and Young’s modulus by back analysis of mining-induced deformation[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 63: 1−11.
[3] KANG K S, HU N L, SIN C S, et al. Determination of the mechanical parameters of rock mass based on a GSI system and displacement back analysis[J]. Journal of Geophysics and Engineering, 2017, 14(4): 939−948.
[4] Yazdani M, Sharifzadeh M, Kamrani K, et al. Displacement-based numerical back analysis for estimation of rock mass parameters in Siah Bisheh powerhouse cavern using continuum and discontinuum approach[J]. Tunnelling and Underground Space Technology, 2012, 28: 41−48.
[5] 冯夏庭, 张治强, 杨成祥, 等. 位移反分析的进化神经网络方法研究[J]. 岩石力学与工程学报, 1999, 18(5): 529−533. FENG Xiating, ZHANG Zhiqiang, YANG Chengxiang, et al. Study on genetic-neural network method of displacement back analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(5): 529−533.
[6] 周冠南, 孙玉永, 贾蓬. 基于遗传算法的BP神经网络在隧道围岩参数反演和变形预测中的应用[J]. 现代隧道技术, 2018, 55(1): 107−113. ZHOU Guannan, SUN Yuyong, JIA Peng. Application of genetic algorithm based BP neural network to parameter inversion of surrounding rock and deformation prediction[J]. Modern Tunnel Technology, 2018, 55(1): 107−113.
[7] 谷淡平, 凌同华, 黄阜. 考虑参数不确定性的台阶式边坡滑面强度参数反演分析[J]. 铁道科学与工程学报, 2019, 16(5): 1186−1193. GU Danping, LING Tonghua, HUANG Fu. Back analysis of strength parameters for the slip surface of stepped slop considering parametric uncertainties[J]. Journal of Railway Science and Engineering, 2019, 16(5): 1186− 1193.
[8] GUO Q Q, PEI L, ZHOU Z J, et al. Response surface and genetic method of deformation back analysis for high core rockfill dams[J]. Computers and Geotechnics, 2016, 74: 132−140.
[9] 高玮. 基于粒子群优化的岩土工程反分析研究[J]. 岩土力学, 2006, 27(5): 795−798. GAO Wei. Back analysis algorithm in geotechnical engineering based on particle swarm optimization[J]. Rock and Soil Mechanics, 2006, 27(5): 795−798.
[10] 孙斌. 基于粒子群−有限差分耦合算法的隧道岩体力学参数反演[J]. 铁道科学与工程学报, 2014, 11(3): 135−139. SUN Bin. Back analysis of physical and mechanical of tunnel based on PSO-FLAC2D[J]. Journal of Railway Science and Engineering, 2014, 11(3): 135−139.
[11] JIA Y F, CHI S C. Back-analysis of soil parameters of Malutang II concrete face rockfill dam using parallel mutation particle swarm optimization[J]. Computers and Geotechnics, 2015, 65: 87−96.
[12] 吴忠广, 吴顺川. 深埋硬岩隧道围岩参数概率反演方法[J]. 工程科学学报, 2019, 41(1): 78−87. WU Zhongguang, WU Shunchuan. Probabilistic back analysis method for determining surrounding rock parameters of deep hard rock tunnel[J]. Chinese Journal of Engineering, 2019, 41(1): 78−87.
[13] Miro S, Konig M, Hartmann D, et al. A probabilistic analysis of subsoil parameters uncertainty impacts on tunnel-induced ground movements with a back-analysis study[J]. Computers and Geotechnics, 2015, 68: 38−53.
[14] 阮永芬, 高春钦, 刘克文, 等. 基于PSO优化小波支持向量机的岩土力学参数反演[J]. 岩土力学, 2019, 40(9): 1−9.RUAN Yongfen, GAO Chunqin, LIU Kewen, et al. Inversion of rock and soil mechanics parameters based on PSO optimization wavelet support vector machine[J]. Rock and Soil Mechanics, 2019, 40(9): 1−9.
[15] 刘忠豹. 通过改进自适应PSO优化BP网络预测大坝变形[J]. 大地测量与地球动力学, 2019, 39(5): 528−532. LIU Zhongbao. Prediction of dam deformation based on the improved BP neural network with adaptive particle swarm optimization[J]. Journal of Geodesy and Geodynamics, 2019, 39(5): 528−532.
[16] 胡军, 董建华, 王凯凯, 等. 边坡稳定性的CPSO-BP模型研究[J]. 岩土力学, 2016, 37(增1): 577−582, 590. HU Jun, DONG Jianhua, WANG Kaikai, et al. Research on CPSO-BP model of slope stability[J]. Rock and Soil Mechanics, 2016, 37(Suppl 1): 577−582, 590.
[17] 何明慧, 徐怡, 王冉, 等. 改进的粒子群算法优化神经网络及应用[J]. 计算机工程与应用, 2018, 54(19): 107− 113, 128. HE Minghui, XU Yi, WANG Ran, et al. Combination dynamic inertia weight particle swarm optimization algorithm to optimize neural network and application[J]. Computer Engineering and Applications, 2018, 54(19): 107−113, 128.
[18] Eberhart, Shi Y. Particle swarm optimization: developments, applications and resources[C]// Proceedings of the IEEE International Conference on Evolutionary Computation. New Jersey: IEEE Press, 2002: 81−86.
[19] 张选平, 杜玉平, 秦国强, 等. 一种动态改变惯性权的自适应粒子群算法[J]. 西安交通大学学报, 2005, 39(10): 1039−1042. ZHANG Xuanping, DU Yuping, QIN Guoqiang, et al. Adaptive particle swarm algorithm with dynamically changing inertia weight[J]. Journal of Xi’an Jiaotong University, 2005, 39(10): 1039−1042.
[20] 吕振肃, 侯志荣. 自适应变异的粒子群优化算法[J]. 电子学报, 2004, 32(3): 416−420. LÜ Zhensu, HOU Zhirong. Particle swarm optimization with adaptive mutation[J]. Acta Electronica Sinica, 2004, 32(3): 416−420.
[21] 刘小军, 张永兴. 浅埋偏压隧道洞口段合理开挖工序及受力特征分析[J]. 岩石力学与工程学报, 2011, 30(增1): 3066−3073. LIU Xiaojun, ZHANG Yongxing. Analysis of reasonable excavation sequence and stress characteristics of portal section of shallow tunnel with unsymmetrical loadings[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Suppl 1): 3066−3073.
[22] 方开泰. 正交与均匀试验设计[M]. 北京: 科学出版社, 2001: 233−246. FANG Kaitai. Orthogonal and uniform experimental design[M]. Beijing: Science Press, 2001: 233−246.
Intelligent displacement back-analysis based on improved particle swarm optimization and neural network and its application
LING Tonghua, QIN Jian, SONG Qiang, HUA Fei
(School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410114, China)
In order to obtain the surrounding rock mechanics parameters for engineering design, an improved adaptive particle swarm optimization with neural network algorithm was proposed to realize the back analysis of tunnel surrounding rock mechanical parameter based on the displacement information of the engineering site. Based on the orthogonal and uniform experimental design method, the training samples were obtained. By dynamically changing the inertia weight and adding particle adaptive mutation, the standard PSO was improved and the network’s weights and thresholds are optimized, which improved the network training speed and prediction accuracy. Combining the non-linear relationship which was established by neural network between the inversion parameters and the measured displacement, the optimal inversion parameters were searched by the improved PSO. This method was applied to the back analysis of YK11+150 section of Liyanlong tunnel. The average relative error between calculated displacement and measured displacement is 5.35%, which indicates that the method is feasible.
tunnel engineering; displacement back-analysis; particle swarm optimization; BP neural network
U452
A
1672 − 7029(2020)09 − 2181 − 10
10.19713/j.cnki.43−1423/u. T20191119
2019−12−12
国家自然科学基金资助项目(51678071)
凌同华(1968−),男,湖南双峰人,教授,博士,从事隧道与地下工程研究;E−mail:lingtonghua@163.com

(编辑 涂鹏)
