基于证据理论和贝叶斯网络的列控车载子系统可靠性分析

张振海，王悦榕，党建武

基于证据理论和贝叶斯网络的列控车载子系统可靠性分析

张振海1，王悦榕1，党建武2

(1. 兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070；2. 甘肃省人工智能与图形图像处理工程研究中心，甘肃 兰州 730070)

针对在列控车载子系统可靠性分析中存在不确定信息、共因失效、恢复机制和降级运行的问题，采用融合证据理论的贝叶斯网络模型对其进行可靠性分析。在分析CTCS-3级列控车载子系统结构的基础上构建故障树，并将故障树转化为贝叶斯网络。利用贝叶斯网络的正向推理能力，综合考虑共因失效和恢复机制因素，结合信任测度和似然测度得到列控车载子系统的可用度并讨论降级运行对系统可用度的影响。利用贝叶斯网络的反向推理能力，得到车载子系统薄弱环节。通过求解重要度，得到存在认知不确定性的基本单元对车载子系统可靠性的影响程度。研究结果表明：该方法增强了贝叶斯网络处理不确定信息的能力，运用该方法得到的评价结果比完全信息条件下得到的更符合实际情况。

可靠性分析；车载子系统；证据理论；贝叶斯网络

CTCS-3级列控系统是根据列车运行情况，对其速度和制动方式等状态进行监督、控制和调整的技术装备，用以监控列车在线路上可靠地运行[1]。车载子系统是列控系统的主要组成部分，分析其可靠性并找出薄弱环节，对提高维修水平、改善系统设计及确保行车安全具有重要的意义。列控车载子系统作为冗余系统，共因失效，恢复机制和系统降级运行是影响系统可靠性的重要因素，且在系统失效的过程中，常常会出现一些不确定性因素，这些不确定性因素对可靠性分析影响同样不可忽略。刘昂等[2-3]通过对系统结构和功能的分析，建立系统的故障树模型，采用动态故障树方法(Fault Tree Analysis)分别对列控系统和列控中心进行了可靠性分析。邸丽清等[4−5]采用Markov模型对CTCS-3级列控系统和列控中心进行了可靠性分析，但故障树分析法解决底事件和逻辑门数量多的系统时，计算精度低，而Markov模型有状态空间爆炸的问题。贝叶斯网络(Bayesian Network)的推理方式和状态描述与故障树分析法相似，但其描述事件多态性和非确定性故障逻辑关系的能力更强，并且容易处理共因失效问题，非常适合于可靠性分析，在铁路信号领域可靠性分析中也有应用[6−7]。上述方法中底事件的故障概率均为精确值，而实际分析过程中，由于知识不完备和数据不完整等问题，容易出现认知不确定问题，从而导致很难得到精确的故障率。然而，证据理论能够以多值映射方法获取概率的上下界，具有处理认知不确定性的能力[8]。张友鹏 等[9]将证据理论应用在了铁路信号系统风险评估中，解决了由于知识不完备等因素导致的不确定性问题。基于此，本文将证据理论引入贝叶斯网络，对存在认知不确定性问题的列控车载子系统进行可靠性分析，弥补了无法得到精确故障率的不足，并且综合考虑共因失效，恢复机制和降级场景对系统的影响。

1 CTCS-3级列控车载子系统概述

1.1 系统构成

CTCS-3级列控车载子系统采用故障−安全设计，对保证行车安全起着重要作用，其功能是接收地面信息和无线信息，生成速度控制曲线，通过与列车实际速度比较，监督列车运行，进行超速防护、人机界面显示等。列控车载子系统构成如图1所示。

图1 车载子系统结构图

1.2 故障树模型

按照分析系统，确定顶事件和边界条件，构建故障树并简化的步骤，首先在分析列控车载子系统结构基础上，选择列控车载子系统故障为故障树顶事件。然后根据系统信息传输关系和结构确定基本事件，其中对系统主要功能实现影响很小的设备不做考虑，关键设备中除了应答器信息接收单元、应答器天线和人机界面为双系冷备冗余，其余均为双系热备冗余。最后根据事件间关系建立地故障树如图2所示。图2中各节点对应的事件名称如表1 所示。

图2 车载子系统的故障树模型

表1 节点和事件名称对应表

2 理论基础

2.1 证据理论

其中：()为事件的基本信任分配函数，表示对本身的信任程度。

2.2 贝叶斯网络

贝叶斯网络是一种描述变量间不确定性因果关系的模型，由节点、有向弧和条件概率表组成，其网络结构要求节点间不能形成闭环。

根据贝叶斯公式给出的条件概率定义：

设变量有个状态：1,2,…,x，由全概率公式可得：

贝叶斯网络具有双向推理能力，正向推理也称因果推理，可以得到系统正常工作或故障的概率。反向推理也称诊断推理，在系统故障条件下，可以得到节点故障的概率。这个特点在故障诊断、可靠性分析等方面有着重要的应用[10−11]。

3 基于证据理论和贝叶斯网络的可靠性分析

3.1 故障树向贝叶斯网络的转化

图3 故障树向贝叶斯网络的转化

3.2 共因失效问题

有2个以上部件由于一个共同原因在短时内失效的现象称为共因失效CCF(Common Cause Failure)。由于列控车载子系统采用冗余设计，所以要考虑共因失效的影响，本文选用因子模型解决共因失效问题[14]。

元件1和具有独立失效率和共因失效率，因子的计算公式为：

图4 考虑共因失效的贝叶斯网络模型

3.3 降级场景问题

CTCS-3级列控车载子系统设置了2和3主控单元，具有等级切换功能。当列车从CTCS-2级区域进入CTCS-3级区域，从CTCS-3级区域进入CTCS-2级区域或者设备故障等情况下要进行等级切换，本文考虑由设备故障引起的系统降级运行。当设备故障引起系统降级运行后，由2主控单元实现系统功能，但2和3主控单元之间保持通信，此时将CTCS-3级列控系统的状态定义为降级状态。如图5所示为3种状态下建立的贝叶斯网络，表示车载子系统，2表示2主控单元，3表示3主控单元。设3=0，3=1和3=2表示正常，故障和降级状态。

图5 3种状态的贝叶斯网络

3.4 可靠度预计

贝叶斯网络的各节点之间存在条件独立性，利用联合概率分布求解顶事件发生概率，即：

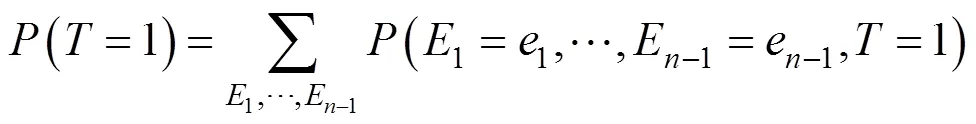
图6 不确定性下的贝叶斯网络模型

通过证据网络的推理，可以求得顶事件发生的信任概率和似然概率，则可得到顶事件实际发生的概率处于两者之间，即有：

3.5 重要度分析

重要度是指系统中部件对顶事件发生的贡献大小，即单元失效对系统失效的影响。在改进系统设计时，重要度是十分有用的信息。记贝叶斯网络中的底事件为E，则3种重要度为：

1) 概率重要度

2) 结构重要度

3) 关键重要度

由于存在不确定信息的底事件有E=1，E=0，E={0,1}3种状态，概率重要度和关键重要度的表达式中的概率为一个区间，所以取信任概率和似然概率的均值进行计算。

显然，在存在认知不确定性的系统中，上述3种重要度无法反映不确定性对系统的影响，故而出现了认知重要度。认知重要度可以反映出底事件的不确定信息对系统可靠性的影响程度，进而采取手段减少其影响。认知重要度作为度量底事件的不确定信息导致顶事件的不确定性的指标，是指在其他底事件不确定度为0时，顶事件发生的信任概率和似然概率之差。

4 CTCS-3级列控车载子系统可靠性分析

假设各单元设备状态相互独立且失效率服从指数分布，取=10%，=1×104，由式(9)计算得到共因失效率，由式(10)计算得到考虑共因失效后各单元失效率。考虑到系统恢复机制的问题，本文取覆盖参数=0.96。由于系统失效过程中存在各种不确定因素，故本文取与失效率均值相差约为10%的值为其左右分布，得到各单元的不确定度如表2所示(CTCS-3级列控车载子系统各单元的失效率数据来源为通号院车载系统工程测试数据和文献[4]和[6])。

采用MSBNx推理软件建立CTCS-3级列控车载子系统的贝叶斯网络如图7所示。

在不考虑3主控单元降级问题时，得到列控车载子系统失效的信任概率和似然概率，如表3所示。由表3可知，列控车载子系统失效的概率区间是[0.000 851%,0.001 040%]，则其可用度区间为[99.998 96%,99.999 149%]。

表2 考虑共因失效的各单元参数表

图7 CTCS-3列控车载子系统的贝叶斯网络

表3 车载子系统失效的概率区间

当考虑3主控单元降级问题时，根据降级原因是由自动闭塞中心RBC或GSM-R通信故障(包括RTU，GSM-R和RSS故障)造成的，RBC的失效率均值为5.00×10−8−1，其余故障率见表2，可得3主控单元处于降级状态下的失效率为3.006×10−5−1。

经过推理可得系统处于故障状态的概率区间为(=1)=[0.000 716%, 0.000 876%]，处于降级状态的概率区间为(=2)=[0.000 300 642%, 0.000 300 643%]，则系统可用度为 [99.996 1%, 99.996 3%]。

通过对比不考虑降级场景的系统可用度可以发现，考虑降级状态的可用度低于不考虑降级状态的可用度，说明降级问题对系统的可用度有较大影响，需减少因故障发生的等级切换问题。

根据贝叶斯网络反向推理，将节点的失效率设置为1，得到各单元的后验概率，如表4所示。由表4可知，失效率较大的是12，10，11，3和8，因此可知人机界面DMI、应答器信息接收单元BTM、应答器天线BTM Ant、列车接口单元TIU、PROFIBUS总线是列控车载系统的薄弱环节。

表4 系统故障时各单元的后验概率

根据式(13)~(16)求出的各单元的重要度如表5所示。由表5可以看出，3，8，9，10，11和12的概率重要度基本相同且较大，说明这6个单元对车载子系统故障的影响程度都很大。其中，12的认知重要度和不确定度都是最大的，所以DMI的认知不确定性对车载子系统可靠性的影响比其他单元要大。

表5 重要度计算结果

本文在传统贝叶斯网络的基础上引入了证据推理，相比文献[6]在完全信息条件下对车载子系统进行的可靠性分析，本文解决了在信息不确定条件下的车载子系统可靠性分析，并综合考虑了共因失效、恢复机制和系统降级因素，更加符合实际情况。

5 结论

1) 根据BN正向推理，结合信任测度和似然测度得到了列控车载子系统失效的可用度区间，并且发现系统因故障降级运行对系统可用度影响较大。

2) 根据BN反向推理，得到车载子系统的薄弱环节有DMI，BTM，BTM Ant，TIU和PROFIBUS总线，其中TIU是双系热备单元，为了降低事故发生的概率，要加强对TIU的检查维护。

3) 通过计算认知重要度，发现对列控车载子系统可靠性分析结果的可信度影响最大的是DMI，为减少认知不确定性的影响，应该采取提高仿真模型准确度等方法重点减小其不确定性。

[1] 中国铁路总公司. CTCS-3级列车运行控制系统[M]. 北京: 中国铁道出版社, 2013: 19−47. China Railway Corporation. CTCS-3 train control system[M]. Beijing: China Railway Press, 2013: 19-47.

[2] 刘昂. 基于动态故障树的列车运行控制系统可靠性分析[D]. 北京: 北京交通大学, 2011. LIU Ang. Reliability analysis of train control system based on dynamic fault tree[D]. Beijing: Beijing Jiaotong University, 2011.

[3] 吴键. 基于动态故障树的列控中心可靠性与安全性分析[D]. 兰州: 兰州交通大学, 2016. WU Jian. Analysisof reliability and safety for train control center based on dynamic fault tree[D]. Lanzhou: Lanzhou Jiaotong University, 2016.

[4] 邸丽清, 袁湘鄂, 王永年. CTCS-3级列控系统RAM指标评价方法研究[J]. 中国铁道科学, 2010, 31(6): 92−97. DI Liqing, YUAN Xiange, WANG Yongnian. Research on the evaluation method for the RAM goals of CTCS-3[J]. China Railway Science, 2010, 31(6): 92−97.

[5] 刘茂婷. 基于动态故障树的列控中心可靠性研究[D]. 成都: 西南交通大学, 2015. LIU Maoting. Reliability research of train control center based on dynamic fault tree[D]. Chengdu: Southwest Jiaotong University, 2015.

[6] 苏宏升, 车玉龙, 张友鹏. 基于贝叶斯网络的列控车载子系统可靠性评估[J]. 中国铁道科学, 2014, 35(5): 96− 103. SU Hongsheng, CHE Yulong, ZHANG Youpeng. Dependability assessment of CTCS-3 on-board subsystem based on Bayesian network[J]. China Railway Science, 2014, 35(5): 96−103.

[7] 江磊, 王小敏, 刘一骝, 等. 基于动态贝叶斯网络的CTCS3-300T列控车载系统运行可靠性及可用性评估[J]. 铁道学报, 2020, 42(3): 85−92. JIANG Lei, WANG Xiaomin, LIU Yiliu, et al. DBN-based operational reliability and availability evaluation of CTCS3-300T onboard system[J]. Journal of the China Railway Society, 2020, 42(3): 85−92.

[8] LIU G Y, ZHANG C Y. Reliability analysis of improved Bayesian network hydraulic system based on evidence theory[J]. Machine Tool & Hydraulics, 2019, 47(24): 17− 23.

[9] 张友鹏, 李远远. 基于云模型和证据理论的铁路信号系统风险评估[J]. 铁道学报, 2016, 38(1): 75−80. ZHANG Youpeng, LI Yuanyuan. Risk assessment of railway signal system based on cloud model and evidence theory[J]. Journal of the China Railway Society, 2016, 38(1): 75−80.

[10] CAI B P, HUANG L, XIE M. Bayesian networks in fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2017, 5(13): 2227−2240.

[11] SONG B H, ZHOU Z B, MA C Q, et al. Reliability analysis of monotone coherent multi-state systems based on Bayesian networks[J]. Journal of Systems Engineering and Electronics, 2016, 27(6): 1326−1335.

[12] 江磊, 王小敏, 蔺伟. 基于动态贝叶斯网络的列控中心可靠性及可用性评估[J]. 交通运输系统工程与信息, 2018, 18(3): 182−217. JIANG Lei, WANG Xiaomin, LIN Wei. Reliability and availability evaluation of train control center based on dynamic Bayesian network[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(3): 182−217.

[13] Simon C, Weber C, Evsukoff A. Bayesian networks inference algorithm to implement Dempster Shafer theory in reliability analysis[J]. Reliability Engineering & System Safety, 2008, 93(7): 950−963.

[14] Hauge S, Hokstad P, Habrekke S, et al. Common cause failures in safety-instrumented system: Using field experience from the petroleum industry[J]. Reliability Engineering and System Safety, 2016, 151(7): 34−45.

[15] 米金华. 认知不确定性下复杂系统的可靠性分析与评估[D]. 成都: 电子科技大学, 2016. MI Jinhua. Reliability analysis and assessment of complex system under epistemic uncertainty[D]. Chengdu: University of Electronic Science and Technology of China, 2016.

Reliability analysis of on-board subsystem of train control system based on evidence theory and Bayesian network method

ZHANG Zhenhai1, WANG Yuerong1, DANG Jianwu2

(1. School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2. Gansu Research Center of Artificial Intelligence and Graphics and Image Processing Engineering, Lanzhou 730070, China)

To deal with uncertain information, common cause failure, recovery mechanism and degraded operation in the reliability analysis of on-board subsystem of train control system, the Bayesian network model integrating evidence theory was used to analyze its reliability. Based on the analysis of the structure of on-board subsystem of CTCS-3 train control system, the fault tree was constructed and transformed into Bayesian network. By using the forward inference ability of Bayesian network, considering the factors of common cause failure and recovery mechanism, the availability of on-board subsystem was obtained by combining the belief measure and plausibility measure. And the effect of degraded operation on system availability was discussed. By using the backward inference ability of Bayesian network, the weaknesses of on-board subsystem were recognized. By solving the magnitude of importance, the effects of basic units with epistemic uncertainties on the system are obtained. The results show that this method enhances the ability of Bayesian network to deal with uncertain information, and the evaluation results obtained by this method are more accordance with the actual conditions than those obtained under the condition of complete information.

reliability analysis; on-board subsystem; evidence theory; Bayesian networks

U283.2

A

1672 − 7029(2020)09 − 2208 − 08

10.19713/j.cnki.43−1423/u. T20200260

2019−12−02

国家自然科学基金资助项目(61763025)；中国博士后科学基金资助项目(167306)

张振海(1983−)，男，河南林州人，副教授，博士，从事交通信息工程及控制、图像处理研究；E−mail：764411629@qq.com

(编辑 涂鹏)