基于LARS 特征选择的风电机组故障诊断的研究
2020-10-15孙群丽刘长良
孙群丽, 周 瑛, 刘长良
(1.华北电力大学 科技学院, 河北 保定 071003; 2.石家庄铁道大学 四方学院, 河北 石家庄 051132;3.华北电力大学 新能源电力系统国家重点实验室, 北京 102206)
0 引言
随着风力发电产业的快速发展,降低机组的故障维护成本受到各方的重视。 有关风力发电机组状态监测和故障诊断的系统相继被开发出来,其中有一部分研究是利用SCADA 数据来进行的。 文献[1]在分析了传动系统故障原理的基础上,选择SCADA 数据中的风速、功率、环境温度和上一时刻的4 个相关温度,一共7 个特征来建立模型,把这7 个特征数据输入到最小二乘支持向量机和高斯混合模型中,以4 个相关温度作为输出,通过输出值来对机组的故障进行分析。 文献[2]分析了风电机组变桨系统在不同工况下的运行特性,用熵优化的邻域粗糙集来对不同工况下的特征进行选择,把选择出来的特征数据代入到以小世界粒子群优化的熵加权学习向量量化模型中,实现对故障的诊断。 文献[3]针对SCADA系统发出故障报警时总是跟随一连串故障的现象,提出用FDA 贡献图法计算出各个特征数据对故障的贡献率,从而实现对故障的定位。 文献[4],[5] 利用自适应神经模糊推理系统分别对机组的变桨系统和整机进行状态监视, 建立了故障模型,针对故障的情况给出警告的输出值。 文献[6]借助于专家经验从SCADA 中选取了几个特征,作为主成分分析模型的输入,通过计算Hotelling-T2 和Q 统计量的斯皮尔曼系数对机组的状态进行监视并识别出功率输出故障。文献[7]用SCADA数据建立机组正常运行的深度神经网络模型,统计分析其误差,确定诊断阈值。
上述文献在利用SCADA 数据的时候没有对所用的特征进行说明,仅仅是依据经验来选择。特征选择的方法分为过滤式、 封装式和嵌入式3 大类[8]。过滤式特征选择方法先对数据集进行特征选择,然后再训练模型,没有考虑其选择出来的特征对后续模型学习的影响。 封装式特征选择方法从初始特征集合中不断地选择特征子集, 训练学习器,根据学习器的性能对子集进行评价,直到选择出最佳的子集, 该方法直接针对给定学习器进行优化,须要多次训练学习器,计算成本很大。 嵌入式特征选择在学习器训练过程中自动地进行特征选择,最小角回归(Least Angle Regression,LARS)算法就是一种嵌入式特征选择方法[9]。 文献[10]利用LARS 在全光谱区进行变量筛选, 得到建模用的特征波长点,提高了模型预测的精度。 文献[11]针对火电厂烟气含氧量的测量环境差、 仪器成本高、测量迟延的问题,利用LARS 从锅炉运行的参数中选择出与烟气含氧量相关的特征参数, 并利用这些参数建立高斯回归模型,实现了烟气含氧量的软测量。 结合上述LARS 算法在非线性系统中的应用, 本文采用LARS 算法对风电机组变桨系统超级电容的参数进行特征选择,对所选择出来的特征数据用K 均值(K-means) 方法对其分类,最后建立隐马尔可夫(HMM)模型对故障进行诊断。 HMM 模型是20 世纪70 年代建立起来的一种时间序列信号的统计分析模型,该模型用不完全统计方法克服了传统统计方法对样本需求量大的不足,并且具有严谨的理论基础,有学者将其应用于故障诊断。
1 基于LARS 的特征选择模型
风力发电机组在把风能转换成电能的过程中,机组的各个部件之间紧密结合,这就导致了众多监测参数之间的互相偶合,利用这些特征参数进行分析时,会造成精确度不高。 为了提高分析的准确性, 本文提出利用LARS 方法来选择问题研究所需的特征[9]。 LARS 方法是一种线性回归方法,基于线性回归平方误差最小,可以从高维数据中选择出重要的特征,使得后续的学习过程仅在一部分特征上构建模型。
给定数据{X,y},X∈Rn×m,y∈Rn,其中xi∈Rn(i=1,2,…,m),寻求最少的变量x1,…,xr,(r≤m)∈Rn,使其线性组合最大程度的接近y,即:
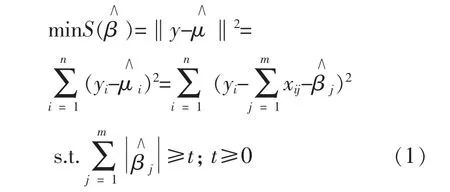

LARS 算法的基本思想是先找出和y 最相关的一个变量xi,将其加入优化模型中,然后在xi所在的方向前进,直到出现另一个变量xj,它和当前残差的相关系数与第一个入选变量xi的相关系数绝对值相同, 此时把xj也加入回归模型中,然后沿着xi和xj角平分线的方向前进,直到找到第3 个变量xk,使得其和(xi,xj)与残差相关性相同,以此类推,直到所需变量均被选入优化模型,在这个过程中残差与所选变量的相关性逐渐减小。
设第k 步时, 被选择出的前k 个变量的集合为A,得到的回归向量为k,对特征矩阵X 标准化,因变量y 中心化,具体算法如下:

(1)初始化k=0,A=φ,μ0=0;(5)重复(2)~(4),直至选到所需个数为止。
以变桨超级电容不平衡故障为例, 利用上述方法进行故障特征的选择。 已知数据中变桨超级电容不平衡故障特征包括电网电压x1、 电网电流x2、电网频率x3、有功功率x4、无功功率x5、变流器直流电压正极x6、变流器直流电压负极x7、变流器直流电流x8、变流器制动电流x9、变流器整流电压x10、变流器直流电流设定值x11、变流器无功功率设定值x12、机舱x 方向振动信号x13、机舱y 方向振动信号x14、 机舱振动有效值x15、 发电机转速x16、发电机转速上限值x17、偏航位置x18、风速x19、发电机转速设定值x20、二阶低通滤波发电机转速x21、陷波滤波后的发电机转速x22、桨距角设定值x23、控制扭矩x24、变桨速率需求值x25、桨距角x26和变桨速率x27。 LRAS 的目标变量为电容不平衡值, 在R 语言中用LARS 对SCADA 中的上述数据进行参数的重要度分析, 在分析过程中进行逐步迭代, 首次迭代时各个特征的标准化回归系数为0,每经过一次迭代系数变化一次,利用R 语言中的summary 函数对各次迭代进行计算,找出最小值对应的各个特征的权重系数β,各权重系数β如表1 所示。

表1 特征对应的权重系数Table 1 Weight coefficients for each feature
由表1 可知,x1,x2, x4, x5, x6, x7, x8, x9, x10,x12,x16,x18,x24,x25和x27的权重系数β 均为0,这表明它们与目标变量的相关性很弱。因此,从上述特征中去除这些项,最后选择出的特征为x3,x11,x13,x14,x15,x17,x19,x20,x21,x22,x23和x26。电网频率、发电机的转速、 变流器信号影响变桨系统超级电容的充电过程,风速、机舱的振动、变桨系统的桨距角影响超级电容的放电过程。
2 HMM 模型
HMM 模型最早被广泛应用于语音识别领域,后续在数字图像处理、生物医学、故障诊断等方面也得到广泛的应用。N,M,π,A,B 为HMM 的模型参数,其含义如下。
N:隐藏马尔科夫链的状态数,在t 时刻所处的状态。已知风电机组的状态是连续变化的,将具有代表性的状态定义为HMM 的隐藏状态。
M:观测向量的个数,O=(o1,o2,…,oM),从一个状态变化转移到另一个状态会导致观测数据的变换, 对观测到的风电机组SCADA 数据进行聚类分析。
π:状态的概率分布,π=(π1,π2,…,πN),其中πi=p(q1=si),1≤i≤N,即在初始时刻t=1 时,N 个状态出现的概率。
A:状态转移概率矩阵,A={aij}N×N;aij=p(qt+1=sj│qt=si),1≤i,j≤N。
B:观测向量概率矩阵,在状态si下观测向量ot出现的概率,B={bj(ot)}N×M,bj(ot)=P(ot│qt=sj),1≤j≤N,1≤t≤M。
风电机组在运行过程中, 状态之间的转移模式会在观测值序列中体现出来。 因此利用上述选择出来的特征观测值序列作为样本进行模型训练,可以得到各个故障的HMM 模型。
在进行机组故障诊断的过程中, 往往是根据观测到的数据O=(o1,o2,…,oT)来判断它属于的故障类型,HMM 在已知故障模型λ 的基础上,通过计算观测数据属于该模型的概率p(O│λ)来进行故障识别。
利用前向算法或后向算法来计算观测序列O在模型下出现的概率。
为了能够对HMM 的参数进行估计,须要利用已知的一组观测向量, 通过递归迭代得到一模型λ,利用Baum-Welch 算法使得p(O│λ)最大[12]。
3 仿真及结果分析
3.1 仿真模型的建立
某1.5 MW 风力发电机, 超级电容为变桨系统提供备用电源。 超级电容由4 个超级电容组串联而成,额定电压为60 V,总容量为108 F,可用能量为150 kJ。NG5 为变桨电机提供总的电源,给超级电容充电时额定输入电压为400 VAC, 额定输出电压为60 VDC,额定输出电流为80 A。 上面有超级电容的充电程度指示灯,红色LED 灯表明处于初始化充电阶段,黄色LED 灯表明已经达到80%的充电量,绿色LED 灯表明已经充满。
NG5 输出电压不正常或损坏、 超级电容损坏、 监测超级电容电压的A10 自制模块KL3404损坏、 电磁刹车继电器或电磁刹车动作不灵敏导致电容充电没有放电、 干扰引起监测电容电压信号跳变、PLC 死机等都有可能导致电容电压不平衡。 现从SCADA 数据中提取出变桨电容电压不平衡数据,共有5 713 组数据,数据分为两部,其中前4 000 组数据作为训练集,后1 713 组数据作为测试集。 HMM 模型中N 为隐藏状态的数目,根据设备的衰退过程将其状态划分为4 个等级,M为观测向量的个数, 观测向量是从现场获取的数据,对这些数据用k-均值方法进行聚类,每一个类别为一个观测种类。 HMM 模型中观测种类的个数会对模型的精确度产生影响, 从训练数据集中取4 组观测数据,每组100 个,用这些构成观测向量, 选择聚类数k 分别为4,5,6,7,8,9 建立对应的模型一、模型二、模型三、模型四、模型五、模型六。图1 为不同模型的建立过程。 由图1 可知:当k 为4 时,模型一实际上经过了500 次的迭代,但是在200 次以后, 得到的对数似然概率在-11上下做微小波动,因此在图中没有进行显示;当k为5 时, 模型二经过163 次迭代达到最大似然概率-2.25,后续的模型经过一定的迭代后也都达到稳定,但是稳定后的最大似然概率均比较低。

图1 变桨系统超级电容不平衡故障模型训练过程Fig.1 Supercapacitor imbalance fault model training process of pitch system
图2 为100 组测试数据在上述不同模型下的匹配程度。

图2 测试数据对模型的识别率Fig.2 The recognition rate of the test data on the model
由图2 可知:模型一有64%的测试数据对数似然概率在-0.1 附近,有30%的测试数据对数似然概率在-3.3 附近;对模型二,大部分测试数据的对数似然概率都在-1.5 上下波动,虽然某些观测值的匹配度与模型一相比低了些,但是在整个测试范围内识别率较平稳,而且与后面的模型相比,对数似然概率也不低。 因此,本文选择模型二为最佳模型。 图3 为整个模型的建立过程。

图3 模型的建立过程Fig.3 Model building process
3.2 结果分析
利用LARS 方法选择出某1.5 MW 风力发电机变桨系统超级电容不平衡故障的原始数据的主要特征。 为了验证选择出的特征对系统的故障识别能力,现将其与原始特征搭建的模型进行对比。首先, 分别利用原始特征数据和经过选择的特征数据训练各自的HMM 模型。然后,利用同样的测试数据在两个模型上验证,验证结果如图4 所示。图4 中: 虚线为利用SCADA 给出的原始特征数据建立的HMM 模型, 该模型对测试数据的对数似然概率最大值为-0.750 3,最小值为-23.861 5,在整个测试过程中波动性比较大; 实线为利用经过选择后的特征建立的HMM-LARS 模型, 在整个测试范围内对数似然概率保持在较高水平做微小波动。

图4 HMM 和HMM-LARS 模型的对比Fig.4 Comparison of HMM and HMM-LARS
为了验证HMM-LARS 模型对故障诊断的有效性, 从变桨位置故障数据和电容不平衡数据中从前向后提取100 组数据, 将这些数据处理后代入到HMM-LARS 模型中, 模型对该故障的识别效果如图5 中虚线所示, 图中实线为该模型对电容不平衡故障的识别率。
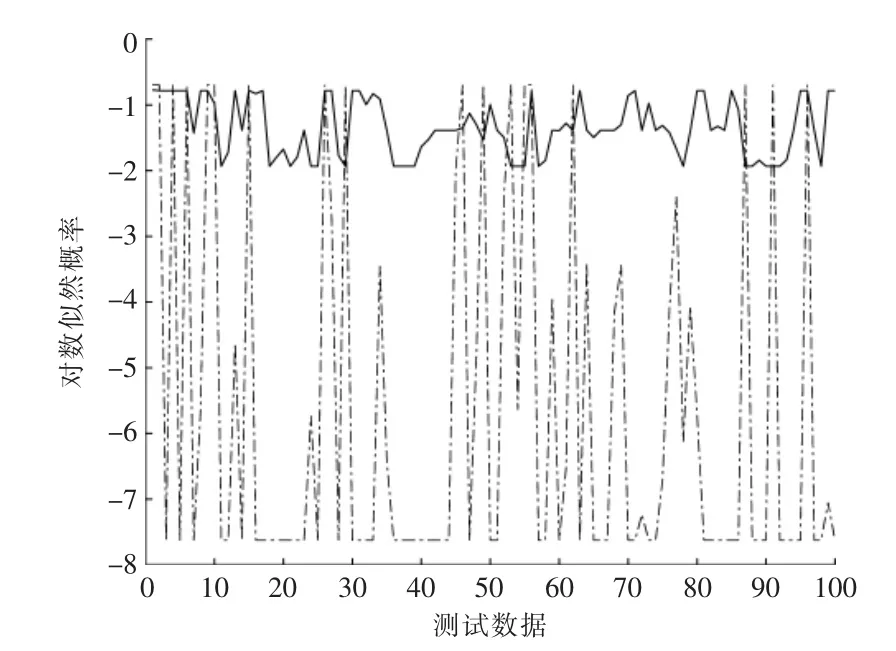
图5 模型对不同故障的识别效果Fig.5 Model recognition effect on different faults
由图5 可知, 用电容不平衡数据建立的模型对其他故障的识别效果比较差, 对电容不平衡故障识别的对数似然概率较高。 在对电容不平衡故障识别的过程中, 模型通过电容在不同状态间的概率来确定其所处的状态, 上述100 组数据在不同状态间的概率分布如图6 所示, 图中4 个状态代表了设备性能逐渐下降的过程。
图6(a)中数据的前部分表示设备性能相对较好,所以对应状态一的概率比较大,随着设备的运行,性能下降,对应状态一的概率也在逐渐地减小,如图中的向下变化的趋势所示。 图6(b)中概率相对比较高的部分出现在第40 个测试数据和第60 个测试数据之间,表明了在这个阶段设备的性能处于状态二。同理可以看出,随着时间和数据的向前推进,图6(c)中最大概率在第60 个测试数据和第80 个测试数据之间,图6(d)中最大概率在第80 个测试数据和第100 个测试数据之间。
从图6(a)~(d)可以看出,设备的性能在不断地退化。 图6 中某一数据段的数据最大概率对应的状态就是该数据段设备所对应的状态, 在最初阶段,图6(a)对应的状态一概率比其他3 幅图高, 这也说明了在最初阶段设备的性能处于状态一, 同理也可看出设备在其他阶段设备所处的状态。
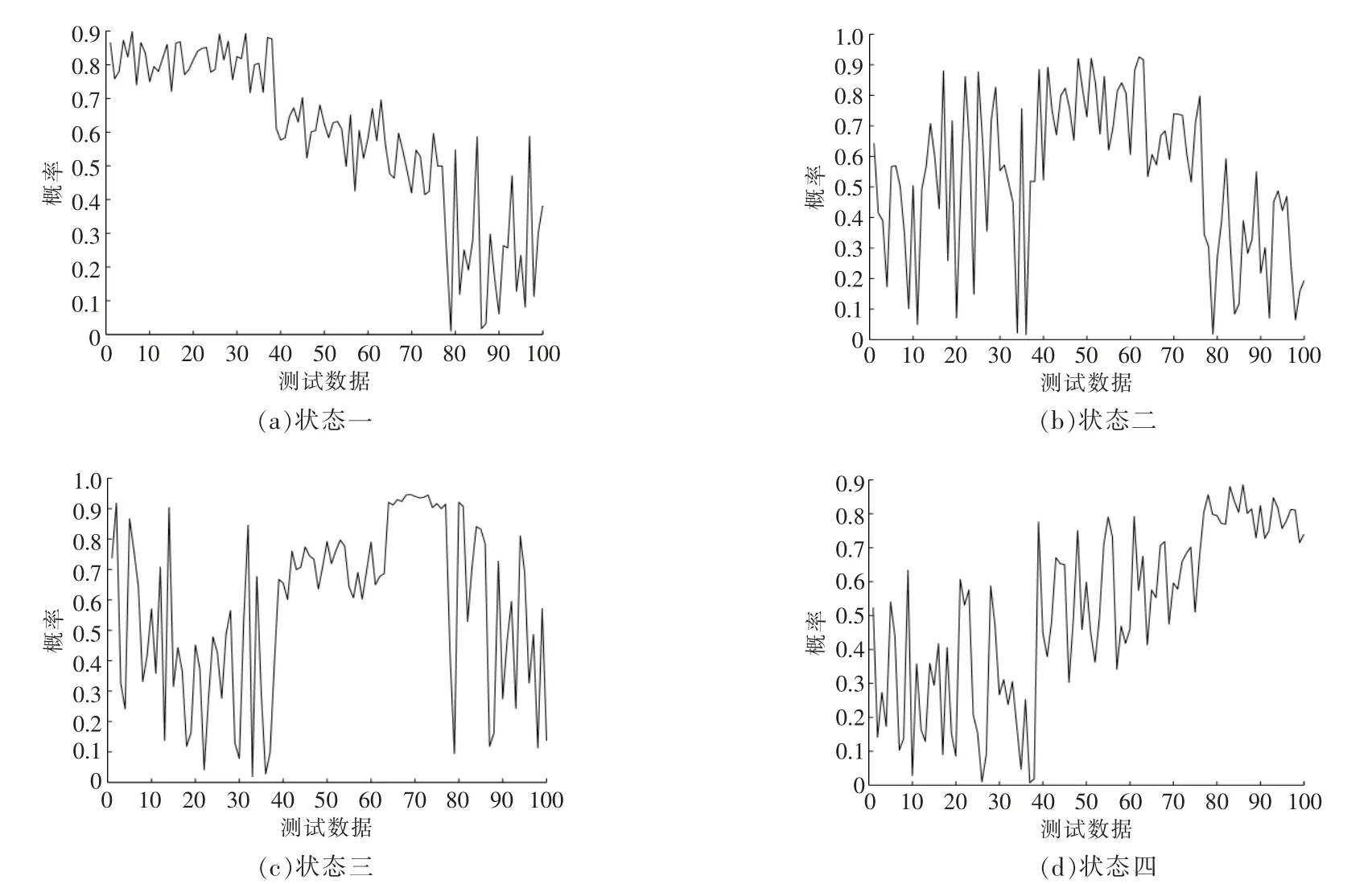
图6 不同状态间的概率Fig.6 Probability between different states
4 结论
在建立风电机组SCADA 数据模型时,针对选用不同的特征数据而导致机组故障诊断和预测时精度不高的问题, 提出了一种基于考虑后续模型优化的特征选择方法, 并在此基础上确定了最优模型的参数。
①根据风电机组运行过程中众多参数间的关系, 以变桨系统超级电容不平衡故障为例,用LARS 特征选择办法找出与电容不平衡的相关特征。
②针对HMM 模型在建模过程中观测向量对模型的影响,设计了观测向量的提取方法,并基于此确定了最优的模型。
③考虑到风电机组在同一部件上出现的多个故障情况,故障之间难以识别的情况,利用其他故障信息来验证所建立模型的准确性。
