基于遗传算法的余割平方波束天线优化设计

燕秀林，段冰，张新刚

1 西安交通大学 城市学院，陕西 西安 710018

2 中国空间技术研究院西安分院，陕西 西安 710100

0 引 言

现代海战中，战机和各类反舰导弹已经严重威胁到舰船的安全，因此实现远距离的目标探测和通信对提升综合作战能力十分关键。在众多的舰载雷达系统中，若是某些雷达和通信设备天线具有水平面窄波束、俯仰面宽波束的方向图特性，则只需转动方位，便可对飞机、导弹等实现远程跟踪定位或者通信。余割平方波束天线由于符合上述要求[1～2]，被广泛应用于舰载雷达系统中。

该类天线包括两大类，一种是柱形的，另一种是非柱形的。前者称为赋形单弯曲反射面天线，后者称为赋形双弯曲反射面天线。赋形单弯曲反射面天线的表面是柱面，但制作线状馈源却难以达到较理想的状态。因此，目前通常采用点状馈源照射的赋形双弯曲反射面天线。

以往对该种天线进行设计时，通常基于几何光学原理和能量守恒定律来确定天线的中截线[3]，然后在此基础上确定整个天线的形面。这种设计方法具有设计速度快、形面光滑连续等优点，但是由于设计过程中没有考虑馈源的相位信息，因此在实际工程应用中，部分区域内天线的性能并不能满足设计要求，需要不断进行调试。

本文将提出一种改进的优化方法，该方法在基于几何光学（GO）原理得到形面的基础上，通过进一步优化反射器形面，从而使天线性能在整个工作角度范围内均能满足设计指标要求。

1 基于几何光学的天线设计方法

目前，常用的双弯曲反射面表面为左右对称设计，对称平面内的横截线称为中截线，其所在的平面称为中截面。

设计双弯曲反射面的基本方法[4～5]为：首先利用几何光学法和能量守恒定律来设计中截线，使天线在俯仰面内能够产生赋形波束，然后才根据聚焦特性生成反射面形状，从而在方位面产生窄波束（图1）。图1 中：O 为馈源相位中心；ρ，ρ1，ρ2分 别 为O 到 中 截 线 上 任 一 点 的 距 离；ψ，ψ1，ψ2分别为入射线与水平线之间的夹角；θ 为辐射角，为正数。根据反射定律，中截线可由下式确定：

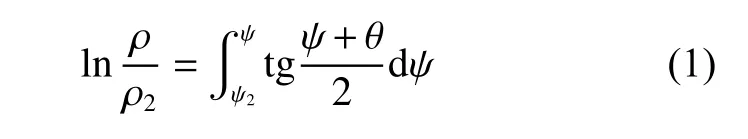
假定馈源的功率方向图为I(ψ)，理想的远区功率方向图为G(θ)，那么由能量守恒定律可知：

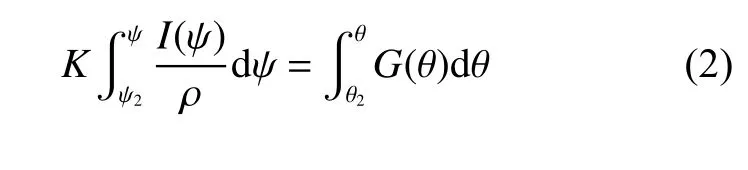
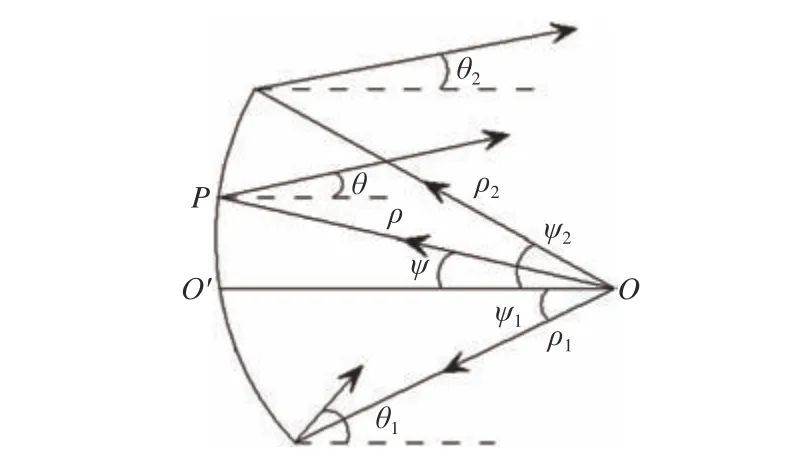
图1 天线中截线示意图Fig. 1 Schematic of centre line of antenna

式中，K 为辐射能量与入射能量的比例系数，其表达式为

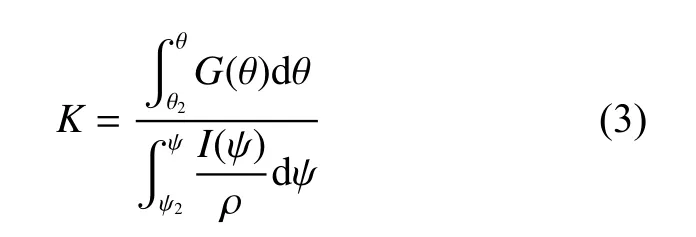
利用上式，经迭代可得到中截线的具体形状。当确定中截线的形状后，用一系列具有聚焦特性的条带来形成反射面，从而使天线在水平面内产生窄波束。形面公式为

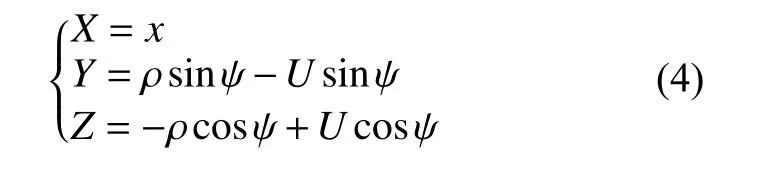
其中，

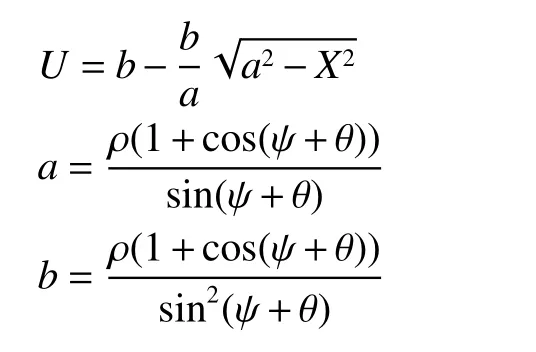
式中：X，Y，Z 为天线反射器形面的三维坐标值；a，b 为中间过程参量。

基于上述方法可以设计出所需的反射面形状，但是由于在设计过程中没有考虑馈源的相位信息，因此测试结果与仿真结果存在一定的差异，影响了实际工程应用。

2 基于物理光学的优化设计方法

在上节设计结果的基础上，采用基于物理光学的优化设计方法进一步优化天线形面。优化时，首先采用3 次样条函数来表示反射面的形变量，具体为[6-7]

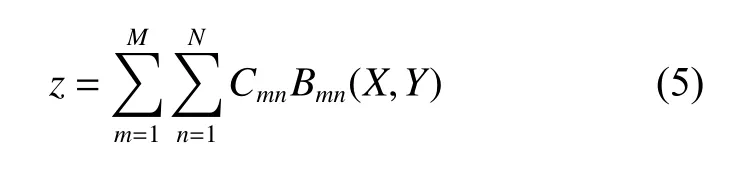
式中：Bmn为3 次样条函数；Cmn为样条函数的系数；M 和N 分别为反射面沿着天线x 轴和y 轴方向划分的网格点数。所有样条函数的系数构成优化变量C，即

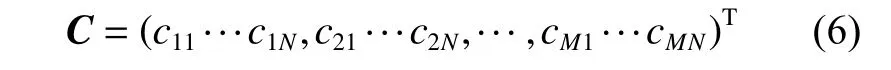
对天线形面进行优化时，采用遗传算法对C 进行优化。

1） 天线分析方法。

余割平方波束天线的电尺寸相对较大，馈源距反射器的距离通常在馈源的远场区，因此可以将反射面局部近似为一个理想的导电平面。根据物理光学等效原理，反射面可以用等效的电流源代替[8-10]：

式中：n 为反射面上任意点指向馈源方向的法向量；Hi为反射面表面的入射磁场。利用物理光学法计算天线远场的计算公式为：

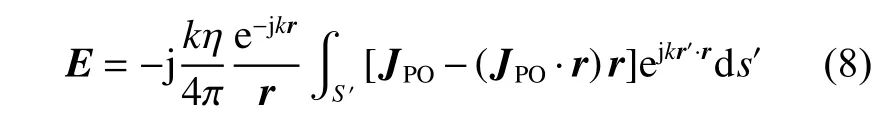
式中：k 和η 分别为波数和自由空间的固有阻抗；S′为反射面；r 为远区场点的位置矢量；r′为点源的位置矢量。

2） 遗传算法。

遗传算法是模拟生物进化论的自然选择和遗传学机理的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该方法具有原理简单、通用性强、具有全局解搜索能力等优点，在天线设计这类组合优化问题中得到了广泛应用。

本文采用实数编码的遗传算法对天线俯仰面内的增益进行优化[11-12]。为了对天线的性能进行评估，在测试区域内放置了J 个观测站点。在设置适应度函数时，除了考虑设计值与设计指标的直接对比外，还要考虑优化后整个角度范围内增益曲线的平滑性，从而尽可能地提高天线的整体性能。因此，在构建适应度函数时兼顾了2 个方面，如下式所示：

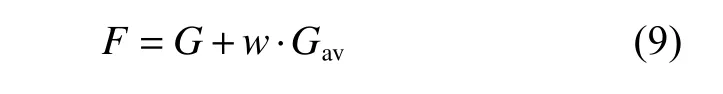
其中，

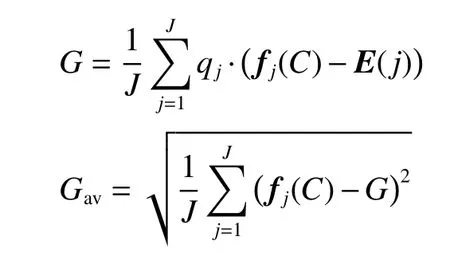
式中：G 为天线增益；Gav为天线平均增益；fj(C)为第j 个观测站点的辐射场；qj和E(j)分别为第j 个观测站点的权值系数和设计要求；w 为平滑度函数，取值通常为0.5～1.6，在下节设计时取为1.2。在设置优化站点时，观测站点的数目不宜过多，否则会影响优化速度；也不宜过少，否则会导致某些角度出现凹陷。qj的选择则依据设计指标中对工作角度范围内增益的重视程度来确定，其中，对于重点保证的区域可以设置为大于1 的常数，一般的区域则直接设置为1。

本文采用式（9）作为优化目标函数，对天线形面具体优化过程为：

1） 编码和种群生成。首先采用二进制编码对由所有样条函数的C 进行编码，构成一个染色体；然后随机产生多个染色体来构建优化的初始种群。

2） 适应度值计算。采用式（9）计算种群中每个个体的适应度值，以评判每个染色体的优劣。个体适应度值越大，则被选择的概率越大，被保存下来的概率也越大。

3） 交叉和变异。随机从种群中选择2 个染色体进行配对，并以一定的概率相互交换部分基因来形成新的个体，这是遗传算法获得优良个体的重要手段。变异则是以一定的变异概率来使选定的变异染色体的某些基因发生反转，是使遗传算法跳出局部最优解的重要手段。

4） 终止。当进化到设定的代数或者最优值连续若干代都没有明显的变化时，则停止优化，并把截止目前优化得到的最优解输出，得到天线的具体形状。

3 设计实例

本案例的目的是设计一种符合特定指标要求的余割平方波束天线，该天线工作在Ka 频段，由反射面和馈源构成。根据设计指标要求和布局限制，口径天线选为0.9 m；为了避免馈源对反射器视场的干涉，天线偏置距离选为1.2 m；天线焦距选为1.35 m；喇叭由TE11 模式激励，喇叭口径为72 mm。

首先，基于几何光学原理编写相应的设计程序，得到天线的初始形面，并利用商用的Grasp10软件对天线进行仿真计算，得到天线的方向图（图2）。图2 中红色虚线为设计指标要求，蓝色实线为基于几何光学方法得到的反射面形状，是利用商用Grasp10 软件计算出的结果。由图中可以看出，在30°～60°内，天线性能比设计要求低了约0.8 dB，在上述角度区间的性能不能满足设计指标的要求。

在以上设计结果的基础上，采用自编的基于实数编码遗传算法程序对反射面形面进一步进行优化，优化后得到反射面形变量相对于标准抛物面的形变量（图3）。

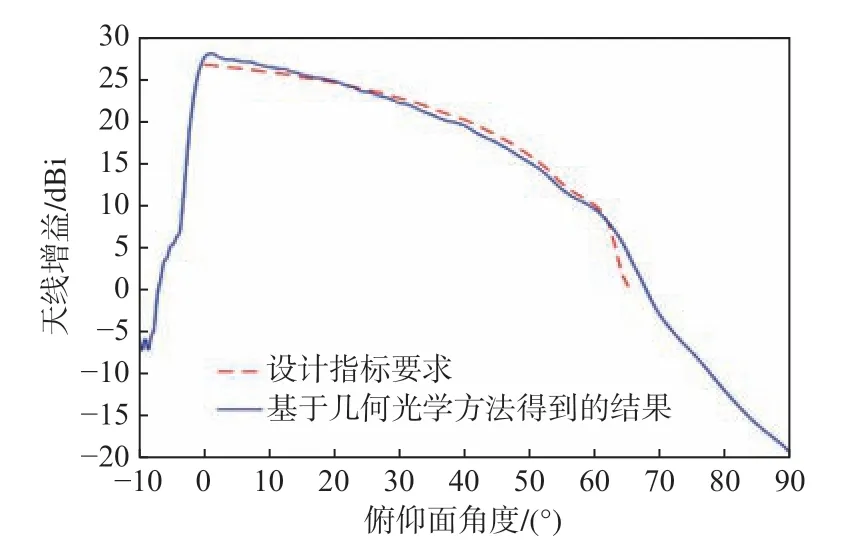
图2 基于几何光学方法得到的结果Fig. 2 Results based on GO method

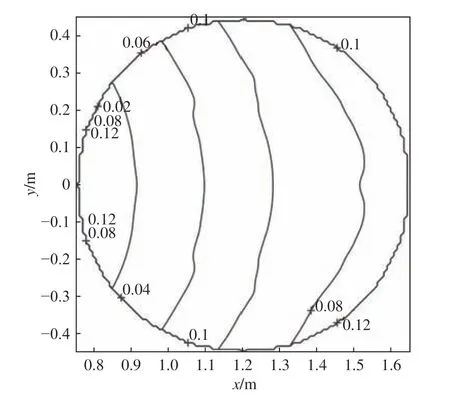
图3 优化后发射面的形变量Fig. 3 Distortion of the reflector after optimization

由图3 可以看出，优化后反射器形面的形变量随天线x 轴方向的增大而逐渐增大，但其相对于标准抛物面的形变量都在0～0.12 m 以内，且整个反射器形面的形变比较光滑，没有发生突变的区域，可满足实际加工要求。

然后，利用商用Grasp10 软件对天线性能重新进行计算，得到的结果如图4 所示。

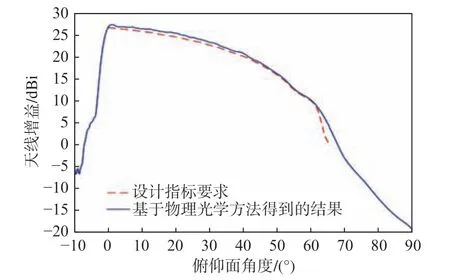
图4 基于物理光学方法得到的结果Fig. 4 Result based on PO method

由图4 可以看出，经过进一步优化后，在0°～70°内天线增益均高于设计指标要求，在30°～60°内，天线增益较之前最大提高了约1.2 dB，更有利于实际工程应用。

4 结 语

本文提供了一种基于物理光学理论的余割平方波束天线优化方法，并对优化过程中需要注意的问题进行了说明。针对一个Ka 频段余割平方波束天线进行了优化设计，并与基于几何光学方法得到的结果进行了对比，结果表明，优化后的天线增益较之前最大提高了约1.2 dB，这说明该方法在此类天线设计中具有优越性。