基于CNYFR的宽带信号接收技术研究

常安琪 徐 伟

(西安电子工程研究所 西安 710100)

0 引言

随着雷达技术的持续发展，多样化的信号形式、多变的调制方式、不断拓宽的雷达信号频段等因素，都将给雷达侦察接收机的设计带来挑战。在复杂的电子侦察环境中，雷达的频谱范围约5 MHz～95 GHz[1]，侦察接收机需具备足够的瞬时截获带宽来接收超宽带雷达信号。

目前，主流的电子战接收机基本上采用了ADC结合数字信道化的宽开截获方案。虽然其具备高灵敏度、全截获概率等优点，但是，ADC器件现有发展水平很难与日益拓展的信号带宽和动态范围相匹配。面对新体制下的超宽带雷达信号带来的挑战，迫切需要通过低速ADC实现宽带信号采集的方案。Nyquist折叠接收(NYFR)结构作为一种典型的新式接收结构[2]，不仅突破了Nyquist采样定理的限制[3]，而且使用较少的资源量实现理论上的瞬时全频段接收。

本文以NYFR结构为基础，对NZ编码式[4]的双谐波本振NYFR进行了研究，对不同信号参数、信噪比条件下的信号载频估计性能进行仿真分析，并对当前算法的技术改进提出了展望。

1 CNYFR

编码式奈奎斯特折叠接收机(Code Nyquist Folding Receiver，CNYFR)，是在谐波本振中加入编码信息，对宽带输入信号进行混频，本振的谐波等间隔地分布在监测带宽内，且每个谐波都有不同的编码调制特征。

1.1 CNYFR结构

CNYFR的实现结构如图1所示。

图1 CNYFR结构示意图

图1中，假设输入信号是单频信号。首先，输入信号通过低通滤波器LPF1，去掉带外噪声，得到信号x(t)；接着，x(t)与pi(t),i=1,2，…，Nb，相乘获得调制信号ri(t)=x(t)pi(t),i=1,2，…,Nb，其中pi(t)表示第i个本振信号，Nb表示本振信号的总个数；然后ri(t)通过低通滤波器LPF2，其中滤波器的带通(-fs/2,fs/2)，fs为ADC的采样频率，得到信号si(t)；最后，对si(t)进行ADC采样，得到si(n)；接着送入DSP进行NZ参数的估计。

本振信号pi(t)的基本参数fs，相位θ(n)和初相φ0由直接数字频率合成器DDS产生。在NYFR结构中，当本振信号个数Nb=2时，引入编码机制，生成宽带调制信号p1(t)和p2(t)，对整个监测带宽内的奈奎斯特区域(Nyquist Zone，NZ)进行划分。首先，将监测带宽Bd划分为N个子带，每个子带的带宽均为K1fs，其中K1为编码因子。相当于把每个子带带宽Bd/N进一步划分为K1个NZ，每个NZ的带宽为Bd/NK1，即Bd=NK1fs。为了得到不同的谐波调制特征，设计p1(t)的带宽分布在每个子带内都相同，子带内各NZ的带宽按照kBθ递增，其中k=1,2,…,K1，Bθ是θ(t)的带宽，θ(t)为本振信号的相位调制函数。根据此规则，p1(t)可以表示为

(1)

其中，φ0为该本振信号初相。

相应地，p2(t)的带宽在各子带间按照nBθ增长，子带内各NZ带宽相同，可得

(2)

θ(t)取二次相位函数

(3)

其中T为信号脉宽。

由式(1)、式(2)、式(3)，可通过参数n、k取值的不同，构成不同的带宽编码信息，从而实现监测带宽内，每个NZ都对应独有的编码方式。例如当子带个数N=2，编码因子K1=5时，具体对应关系如表1所示。

表1 本振相位调制函数表

1.2 数学模型

以捷变频信号为例，x(t)可以表示为

(4)

NYFR的关键在于将带宽输入信号位于不同的NZ成分搬移至基带，根据本振信号在各NZ的不同调制信息，从NYFR的输出中获得输入宽带信号的信息。那么，可以采用式(1)、式(2)作为本地调制信号的形式，对应的最大截获带宽为

BI=(NK1+1/2)fs

(5)

混频后经LPF2滤波可以得到

(6)

(7)

从式(7)可以看出，kJ,q表征待检测信号频率所属的子带，kI,q表征待检测信号所属某子带中的间隔，也证明了这两编码信息可以确定唯一的NZ，推导可得

kH,q=kI,q+K1(kJ,q-1)

(8)

对s1(t)、s2(t)采样得

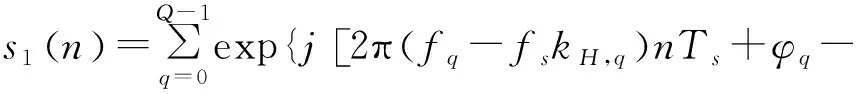
(9)

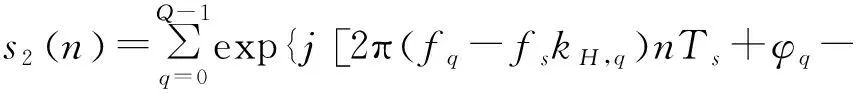
(10)

其中，Ts=1/fs为采样间隔。

从式(9)可以得出，在输出s1(n)中，第q个子脉冲对应的信号为宽带信号，其中心频率、带宽和初始相位分别为fq-fskH,q、Bs1=kI,qBθ和φq-kH,qφ0。同理从式(10)可以得出，在输出s2(n)中，第q个子脉冲对应的信号也为宽带信号，其中心频率、带宽和初始相位分别为fq-fskH,q、Bs1=kJ,qBθ和φq-kH,qφ0。s1(n)和s2(n)具有相同的中心频率、初始相位，但是信号带宽不同。

1.3 频率不混叠条件

信号s1(t)和s2(t)的频率分量分布在频率为[-fs/2,fs/2)的Nyquist域中，由于kI,q∈{1,…,K1}，根据Nyquist采样理论，采样不混叠的条件是

(11)

1.4 NZ估计

由1.2可得经过本振调制后最终能获得载频为fCNYFR=fq-fskH,q的信号，其频点由fq、fs和kH,q共同决定。在对奈奎斯特区域进行估计之前，假设已通过相关算法对检测信号的有无进行检测。本文首先计算s1(n)的时频分布PWVD，然后检测时频分布脊线的幅度来估计信号带宽，定义[5]如下

(12)

其中，h(τ)为窗函数。

由时频分布求解奈奎斯特区域的过程可分为4个步骤，如图2所示。

图2 NZ估计流程

(13)

为了更好地评估上述算法的性能，引入频率估计的正确判决率(PCD)[6]和归一化均方根误差(NRMSE)这两个概念，具体定义为

(14)

(15)

其中RT为正确判决次数，ST为总实验次数，本文中频率估计正确的标准为|fk-f|≤0.01 GHz，ST取100；f为被估测参数真值，fk为参数估计值。

2 CNYFR仿真研究

仿真条件：信号载频fq，基础调制带宽Bθ，信噪比SNR，子带个数N=2，编码因子K1=5，检测带宽Bd=2 GHz，采样频率fs=0.2 GHz。

2.1 本振信号

本振p1(t)、p2(t)的频谱图如图3所示。

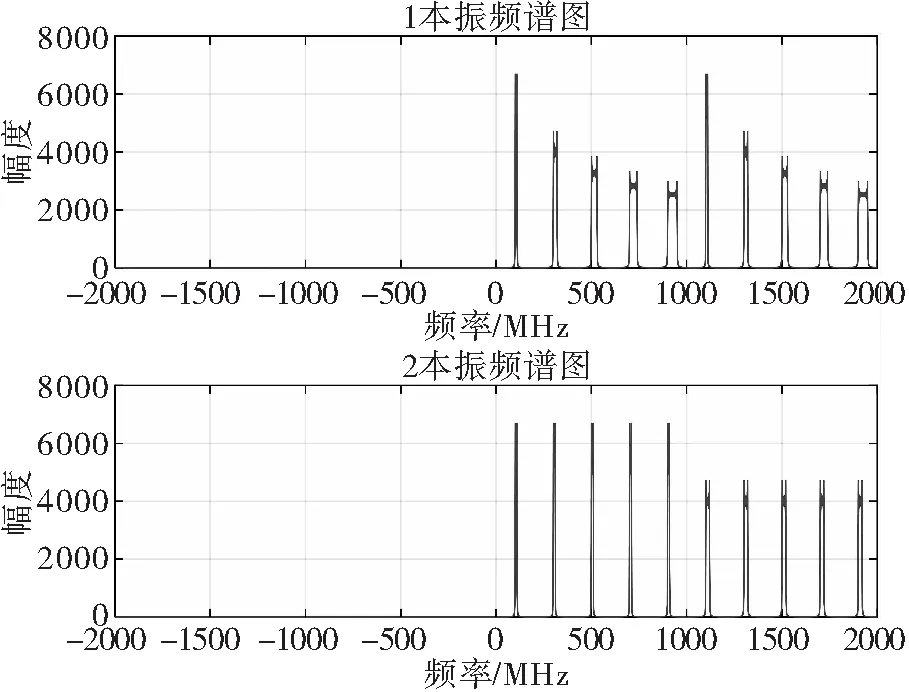
图3 本振信号频谱图

从图3中可以看出，p1(t)的频谱以5为周期重复出现，且带宽逐渐增加；p2(t)的谐波带宽只有2种，每一种频谱都对应p1(t)的一个周期，与表1的理论结果相吻合。

2.2 待检测信号

1)假设待检测信号为单频信号，信号载频fq=0.68 GHz，基础调制带宽Bθ=5 MHz。在无噪声条件下，可以得出待检测信号调制后的仿真图。

2)假设待检测信号为单频信号，信号载频fq=0.68 GHz，取变化的调制带宽Bθ=1～20 MHz作为自变量进行仿真。在无噪声条件下，可以得出待检测信号调制后的仿真图如图5所示。

图4 频域和时频图

图5 待检测信号调制后的仿真图

由图5(a)、图5(b)可以得出，在已知仿真条件下，当本振信号带宽在频谱不混叠范围内变化时，载频估计值在其真值附近上下浮动，估计误差也可以保持在一个很小的范围内。而且，信号载频的估计效果与本振带宽的变化之间并不具备明显的线性关系，呈现出一种不规则的波动。

3)假设待检测信号为单频信号，信号载频fq=0.68 GHz，基础调制带宽Bθ=5 MHz。在信噪比SNR取[-5,10]dB的条件下，可以得出PCD随SNR变化趋势仿真图和NRMSE随SNR变化趋势仿真图。

如图6(a)所示，当信噪比SNR≥-1 dB时，奈奎斯特区域的正确判决率PCD可达90%以上；如图6(b)所示，当信噪比SNR≥0 dB时，归一化均方根误差值NRMSE将小于0.05，可见该计算方法的性能良好。

4)假设待检测信号为LFM信号，信号载频fq1=0.68 GHz，fq2=0.84 GHz，fq3=1.26 GHz，带宽分别取5 MHz、10 MHz和15 MHz，本振p1(t)、p2(t)的形式取式(1)、式(2)，基础调制带宽Bθ=5 MHz。信噪比SNR=5 dB，可以得出待检测信号调制后的仿真图如图7所示。

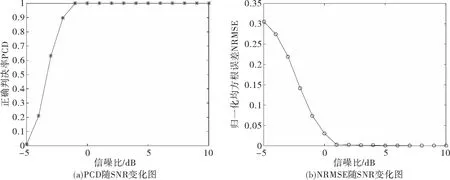
图6 PCD与NRMSE随SNR变化图

图7 待检测信号调制后的仿真图

如图7(b)所示，即便在信噪比较小的条件下，时频线的分布依然可以判断出信号的个数为3，通过论文中的方法可估计得信号载频分别为0.6793 GHz、0.8395 GHz和1.2597 GHz，这与预设值是基本一致的。因此可以说明，该方法不仅适用于单载频信号，也适用于LFM信号。

5)假设待检测信号为单频信号，信号载频变化范围fq=[0.11∶0.01∶2]GHz，基础调制带宽Bθ=5 MHz。在无噪声条件下，可以得出待检测信号调制后的仿真图如图8所示。

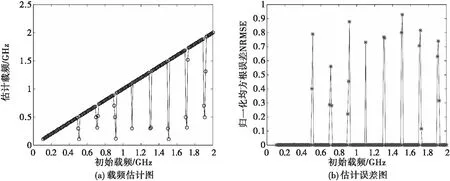
图8 待检测信号调制后的仿真图

如图8(a)、图8(b)所示，当原始信号的载频在[0.11,2]GHz之间变化时，大多数频率点能够实现正确估计，但在部分频率点，如0.5 GHz、0.7 GHz和0.9 GHz等附近的频率点，估计载频与初始载频有较大的偏差，相应的误差值也很大。可以看出，错误估计的频率点正好处于NZ的边缘，说明估计结果的正确性由待检测信号的载频和NZ的选取共同决定。

3 CNYFR算法总结

通过1、2节对CNYFR算法的研究与仿真，总结结论如下：

1)CNYFR算法对于单载频信号和LFM信号都有良好的估计效果。

2)由于每一个NZ都具备独有的编码调制信息，因此当同时存在多个待检测信号时，依然可以通过其不同的调制特征进行识别和估计。

3)在带宽不混叠的约束条件下，不同的本振带宽选取对信号载频的估计影响不大，不具备明显趋势。且针对不同的信号载频，不同的本振带宽估计性能也不同。

4)在不同SNR条件下，信号频率的估计效果也不同。显然，SNR越大，恢复效果越好。本文中的CNYFR算法，在SNR=0dB的条件下，已基本能实现正确识别。

5)若信号载频落在NZ的边缘，对于信号所属的NZ判断会发生偏差，文中方法将无法给出正确的估计结果。

4 CNYFR技术展望

本文主要研究了基于NZ编码的NYFR改进型结构，采用LFM信号作为本地调制信号，对本振带宽分布方式进行编码，提高了NYFR接收机的监测带宽，获得更优的NZ及频率估计性能。同时，给出了基于3 dB带宽的奈奎斯特区域估计方法，取得了良好的效果。然而，从理论分析和仿真结果来看，CNYFR算法结构依然存在着一些问题。

1)Nyquist边缘区模糊，即NZ边缘处区域存在性及唯一性问题。

2)在信号个数多、信号形式复杂和外部噪声共同存在的条件下，CNYFR结构的适应性较差，容易发生频谱混叠、无法提取初相信息等问题。

3)为了使不同的NZ都具备其独有的编码信息，在设计本振信号时需要考虑到满足要求的边界条件，边界条件越明晰，估计结果也会更准确。文中的方法，是以频谱不混叠为边界条件，对不同频率的信号，普遍适用性较差。

因此，一方面，CNYFR结构未来应着重研究Nyquist边缘区域的解模糊问题，探索NZ存在且唯一的充要条件，并以此来调整目前本振信号的编码形式，从而实现对于待检测信号理论接收范围内的全频段估计。另一方面，CNYFR结构应进一步适配复杂多信号接收的情况，对接收信号降噪处理、实现多信号分选和临界条件的进一步细化等方面可以展开研究。