高考数学命题题源探究

◇ 张玉良

“年年岁岁题相似，岁岁年年人不同．”每一届高三学生都会好奇高考题是如何命制的，高考命题题源在哪．如果能弄清楚这两个问题，高三的备考就更有针对性了．笔者通过对2019年全国卷及独立命题的省市高考题进行归纳、整理，得出了高考命题的几个重要来源，供高三考生备考参考．

1 源于教材

教材是教师教学、学生学习的主要依据，教材中包含了学生必须要掌握的内容，其中例题、习题具有很强的代表性，因此教材也成为高考命题的重要依据．不难发现，很多考题都是以教材中的例题或习题为背景，通过改编得到的，因此对教材的深入探究是高考备考的重要内容．

例1(2019年全国卷Ⅲ)设F1，F2为椭圆C:的两个焦点，M为C上一点且在第一象限．若为等腰三角形，则M的坐标为

设F1，F2分别为椭圆的左、右焦点，由已知得a＝6，c＝4．设点M(x0，y0)，因为点M在第一象限，所以且MF1＞a＝6，0＜MF2＜6，又F1F2＝2c＝8，所以△MF1F2是以MF2为底边的等腰三角形，所以MF1＝F1F2＝8，MF2＝4．所以点M即为方程(x0＋4)2＋y20＝64与在第一象限的解，联立两方程解得x0＝3或21(舍)，则，故点M的坐标为

考题探源(人教版《选修2-1》课后练习)已知F1，F2是椭圆的两个焦点，点P在椭圆上，如果△PF1F2是直角三角形，求点P的坐标．

2 源于各市、区的模拟题

各市、区的模拟考试是参照考纲要求、命题原则命制试题的，是在高三各个复习阶段检测考生复习情况的阶段性考试，试题的针对性较强，因此往届的模拟考试试题也成为高考命题人参考的重要资料．

例2(2019年全国卷Ⅱ)设f(x)的定义域为R，满 足f(x＋1)＝2f(x)，且 当x∈(0，1]时，f(x)＝x(x－1)．若对任意的x∈(－∞，m]，都有则m范围是( )．

因为当x∈(0，1]时，f(x)＝x(x－1)，又因为f(x＋1)＝2f(x)，所 以f(x)＝2f(x－1)，即将f(x)的图象向右平移1个单位，且图象的纵坐标变为原来的2倍，如图1所示．

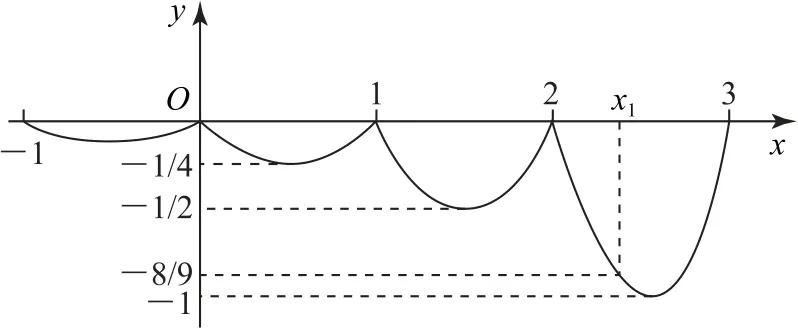
图1

当2＜x≤3时，f(x)＝4f(x－2)＝4(x－2)·．因为x∈(－∞，m]时成立，所以．故选B．

考题探源定义在(0，＋∞)上的f(x)满足:①当x∈[1，3)时，f(x)＝1－|x－2|；②f(3x)＝3f(x)．设关于x的函数F(x)＝f(x)－a的零点从小到大依次为x1，x2，…，xn，…．若a＝1，则x1＋x2＋若a∈(1，3)，则

3 源于往届的高考题

对往年高考题进行改编和创新是高考命题的另一种重要形式，有时将题目条件进行改编，有时对所求结论或问题背景进行改编．

例3(2019年江苏卷)从3名男同学和2名女同学中任选2名同学参加志愿者服务，则选出的2名同学中至少有1名女同学的概率是

从3名男同学和2名女同学中任选2名同学参加志愿者服务，不同的选法共C25＝10种情况．选出的2名同学中至少有1名女同学的情况有两种:选出2名女同学，有C22＝1种选法；选出1名女同学，1名男同学，有C13C12＝6种选法．

考题探源(2018年全国卷Ⅰ)从2名女生和4名男生中选3人参加科技比赛，且至少有1名女生入选，则不同的选法共有种(用数字填写答案)．

4 源于竞赛试题

从内容来看高考与各级各类竞赛互为补充，因此高考命题参考竞赛命题也就不足为奇了．

例4(2019年全国卷Ⅱ)已知点A(－2，0)，B(2，0)，动点M(x，y)满足直线AM与BM的斜率之积为．记M的轨迹为C．

(1)求C的方程；

(2)过原点O的直线交C于P，Q，点P在第一象限，PE⊥x轴，垂足为E，连接QE并延长交C于点G．

(ⅰ)证明:△PQG是直角三角形；

(ⅱ)求△PQG面积的最大值．

(2)(ⅰ)设直线PQ的斜率为k(k＞0)，则其方程为y＝kx，将 其 与 曲 线C的 方 程 联 立，得x＝则P(t，tk)，Q(－t，

于是，直线QG的斜率为方程为t)，将其与C的方程联立，得

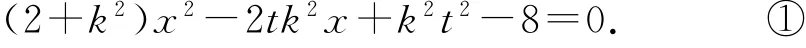
令G(xG，yG)，则－t，xG是方程①的解，所以所以PQ⊥PG，△PQG是直角三角形．

(ⅱ)△PQG的面积的最大值为

考题探源已知直线x－y＋1＝0经过椭圆S:的一个焦点和一个顶点，过原点O的直线交椭圆S于点P，A，其中点P在第一象限，过P作x轴的垂线，垂足为S，延长AC交椭圆S于点B，求证AP⊥BP．