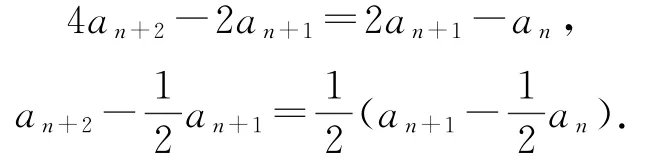由一道教材习题谈解题后的反思

◇ 马中明

解题后的反思是帮助学生巩固所学知识、提高分析和解决问题能力的重要方式，但反思的内容是什么，众说纷纭．教学中，笔者采用反思不同解法、反思解法优化、反思一般结论、反思问题根源等方式，取得了较好的教学效果．现以人教A版教材中一道数列习题为例谈解题后的反思，与广大同行分享．

1 问题呈现

例1(人教A版数学《必修5》数列习题)已知数列{an}，a1＝5，a2＝2，an＝2an－1＋3an－2(n≥3)，对这个数列的通项公式进行研究，能否写出它的通项公式?

本题是在学生学习了数列的递推关系an＋1＝f(an)后，出现的一道三项递推关系问题．对于两项递推关系问题，我们常采用构造法，构造出特殊的等差或等比数列再求解．其实，对于三项递推关系同样可以采用这种方法．

2 问题解答

根据an＝2an－1＋3an－2(n≥3)的结构特殊，将等式两 端 同 时 减3an－1，得an－3an－1＝－(an－1－3an－2)，进而可得数列{an＋1－3an}是以a2－3a1＝－13为首项，－1为公比的等比数列，所以an＋1－3an＝－13×(－1)n－1，进而得出相邻两项的递推关系．

将式an＋1－3an＝－13×(－1)n－1两边同时除以

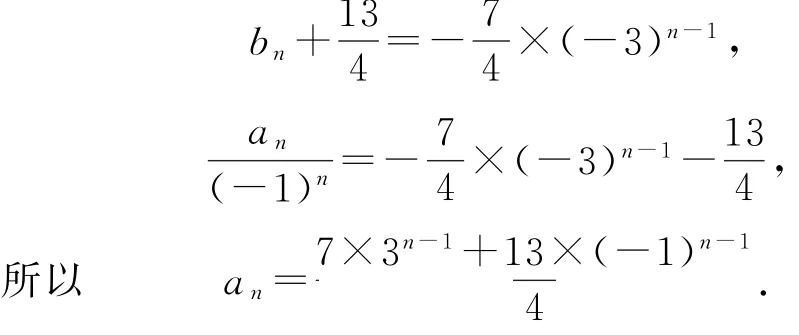
3 解题反思

3.1 反思不同解法

反思1在得出an＋1－3an＝－13×(－1)n－1后，两边同时除以3n＋1，得

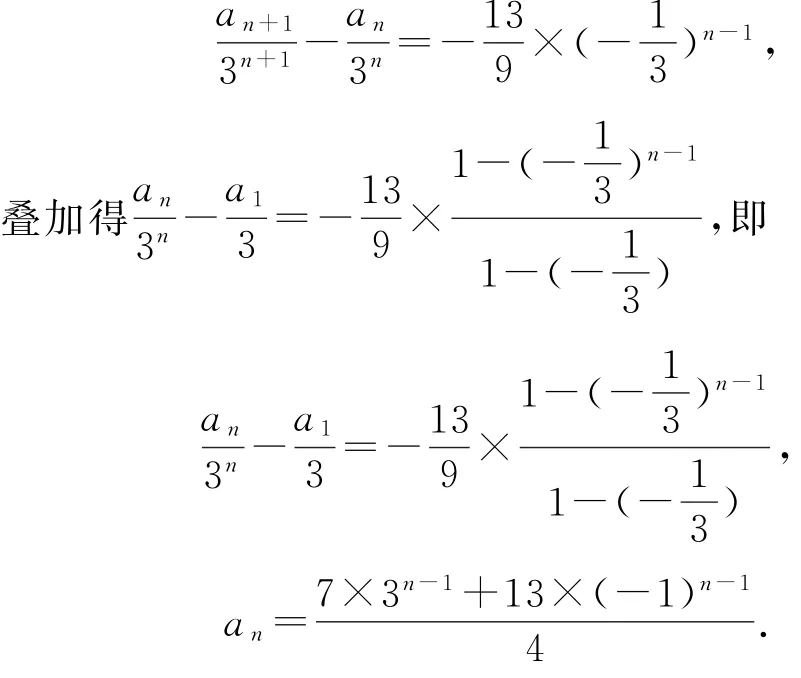
反思2如果所给递推关系不易观察出构造方法，可利用待定系数法处理，即令an－san－1＝t(an－1－，从而可得数列{an＋1－san}是以a2－sa1为首项，t为公比的等比数列．

此方法在“反思一般结论”中有详细说明，此处不再赘述．

3.2 反思解法优化

反思3将an＝2an－1＋3an－2(n≥3)两端同时减3an－1，得an－3an－1＝－(an－1－3an－2)，进而可得数列{an＋1－3an}是以a2－3a1＝－13为首项，公比为－1的等比数列，所以

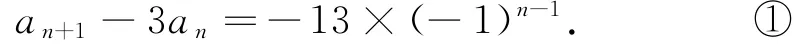
将an＝2an－1＋3an－2(n≥3)两端同时加an－1，可得an＋an－1＝3(an－1＋an－2)，进而可知数列{an＋1＋an}是以a1＋a2＝7为首项，3为公比的等比数列，所以an＋1＋an＝7×3n－1，与式①相减得

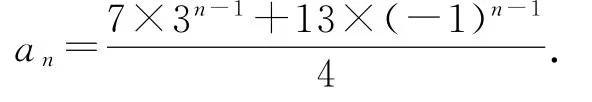
3.3 反思一般结论

反思4将问题推广到一般情况，即已知数列{an}的前两项为a1，a2，且an＝pan－1＋qan－2(n≥3，p，q为非零常数)，求{an}的通项公式．

解设an－san－1＝t(an－1－san－2)，与原式对照得s＋t＝p，st＝q，进而可得即{an＋1－san}是首项为a2－sa1、公比为t的等比数列，所以an＋1－san＝(a2－sa1)tn－1．两边同除以sn＋1得叠加得即

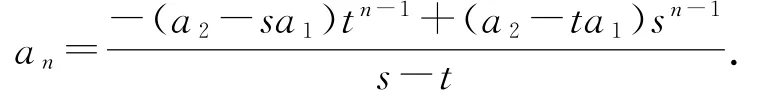
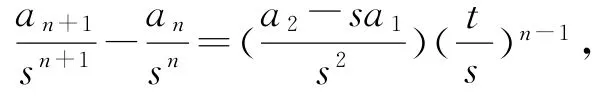
3.4 反思问题根源

反思5本题的根来源于著名数列——斐波那契数列，F1＝1，F2＝1，Fn＝Fn－1＋Fn－2(n≥3)．

解利用一般结论中的求解方法，s＋t＝1，st＝－1，构造一元二次方程x2－x－1＝0，解得s＝代入一般结论中可得斐波那契数列的通项公式

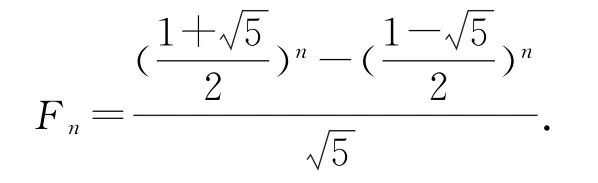
综上，针对不同的问题，反思的视角往往也不尽相同，教学中教师要有意识地引导学生进行反思，这对学生知识的巩固及能力的培养都大有益处．

3.5 反思问题的变式

反思6已知数列{an}的前n项和为Sn，n∈且当n≥2时，4Sn＋2＋5Sn＝8Sn＋1＋Sn－1．求数列{an}的通项公式．

解利用反思3中的构造法，将4Sn＋2＋5Sn＝8Sn＋1＋Sn－1，变 形 得4Sn＋2－4Sn＋1＋Sn－Sn－1＝4Sn＋1－4Sn(n≥2)，即4an＋2＋an＝4an＋1，即