应用之线参数方程解题的几个关注点

◇ 金玉明

直线的方程有点斜式、斜截式、两点式、截距式、一般式等多种形式，直线的参数方程是同一坐标系中直线方程的另外一种表示形式，其本质是借助参数变量来表示直线上的点．参数方程的引入为解析几何问题的求解又提供了一种重要的途径．本文就直线参数方程学习中的关键点及其应用进行例析，以供学生学习参考．

1 关注参数t的几何意义

设直线l过点M0(x0，y0)，倾斜角为

直线l上任一点M(x，y)到M0(x0，y0)的距离为|t|，若M在M0上方，则t＞0；若M在M0下方，则t＜0；若M与M0重合，则t＝0．因此点M(x，y)的坐标可表示为这就是直线l的参数方程，其中t为参数．应用参数方程中参数t的几何意义可简捷处理直线与曲线相交问题中的弦长、弦的中点等问题．

例1在直角坐标系xOy中，抛物线C:y2＝2px(p＞0)，过点(－2，－4)且斜率为1的直线l．设曲线C与直线l交于M1，M2，若求p．

设直线l参数方程为为参数)，设M1，M2的参数分别为t1，t2，将l的参数方程代入C:y2＝2px，得0，Δ＞0，所以

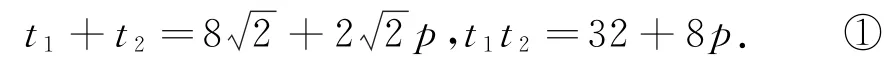
假设直线l与曲线y＝f(x)交于两个点M1，M2，对应的参数分别为t1，t2，M0(x0，y0)为直线l上一定点，则

2 关注参数方程一般式与标准式的区别

直线l的参数方程为 参 数)，(x0，y0)为直线l所过的定点．若a2＋b2＝1，则为参数方程的标准形式，否则为一般形式，一般方程中的参数，不具有t的几何意义．欲应用参数t的几何意义进行解题，需将一般方程化为标准形式．

例2直线l的参数方程为为参数)，直线l与圆C:(x＋3)2＋(y－1)2＝6交于点A，B，求|AB|的值．

将直线l的一般参数方程为参数)化为标准方程，得为参数)．将

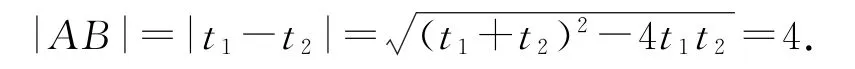
本题求解中若直接将l的参数方程为参数)代入圆C:(x＋3)2＋(y－1)2＝6的方程求解，则会得出错误结论．一般方程为参数)化为标准方程得

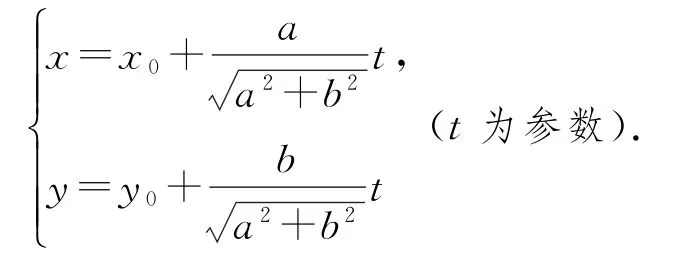
本题的求解也可将直线的参数方程化为普通方程，利用平面几何知识求解．

3 关注参数方程与普通方程的转化

直线的参数方程与普通方程之间的转化具有相互性，解题中并不局限于一定要将参数方程化为普通方程，也可根据题目条件，将普通方程化为参数方程，再利用参数的几何意义往往可使解题过程化繁为简．

例3已知曲线C1的方程为x2＋y2＝1(y≥0)，曲线C2的方程为x2＋y2＋2y＝0．若P是C1上任意一点，过点P的直线l交C2于点M，N，求|PM|·|PN|的取值范围．

方法1设P(x0，y0)，M(x1，y1)，N(x2,y2)．若l的斜率不存在，则

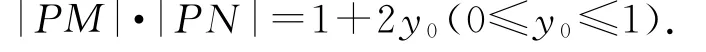
若l的斜率存在，设l方程为y＝k(x－x0)＋y0，与C2的方程联立得

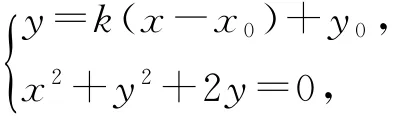
消去y得kx0)2－1＝0．由根与系数的关系得

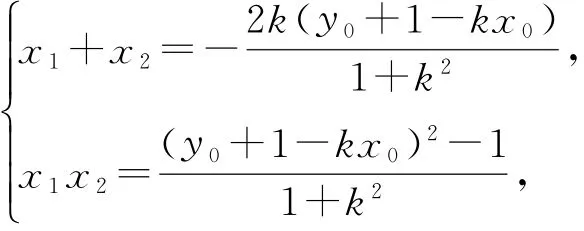
所以

方法2设P(x0，y0)，l的倾斜角为θ，则l的参数方程为为参数)．设M，N对应的参数分别为t1，t2，将代入C2的方程得

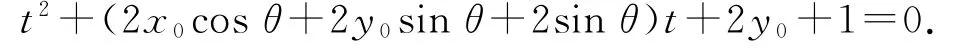
由参数t的几何意义得所以

方法1直接利用曲线的直角坐标方程进行求解，思路直观，学生容易想到，但涉及的计算量较大．方法2借助直线的参数方程及参数的几何意义进行求解，计算简捷．

总之，直线的参数方程是直线方程的重要组成部分，参数方程的应用不仅提升了学生的解题能力，通过对题目条件的分析、构造参数模型，还培养了学生数学建模的核心素养，从而提高学生的数学应用能力，增强学生的创新意识．