交会成就精彩——赏析定积分的交会命题

◇ 李 勇

定积分是新课标教材的新增内容，其基本思想是通过无限分割、近似替代、求和、取极限来达到计算的目的．在高考中，往往重点考查运用定积分的几何意义、基本性质和微积分基本定理等进行积分计算．定积分的几何意义是求曲边图形的面积，在高考试题或模拟试题中基本都是围绕这一视角命题的．本文从定积分与其他知识的交会点出发，赏析其命题亮点．

1 与解析几何的交会

例1已知抛物线W:y＝ax2经过点A(2，1)，过A作倾斜角互补的两条不同直线l1，l2．

(1)求W的方程及准线方程；

(2)当l1与W相切时，求l2与W所围成封闭区域的面积．

(1)由于A(2，1)在抛物线W:y＝ax2上，所

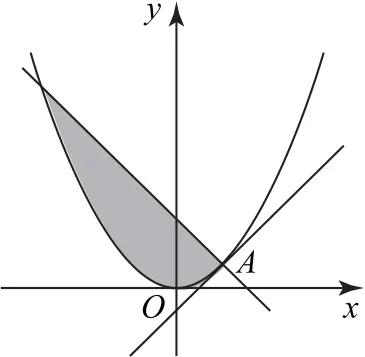
图1

(2)当l1与W相切时，由y′|x＝2＝1，可知l1的斜率为1，所以l2的斜率为－1，所以l2的方程为y＝－x＋3，将其代入W的方程，得x2＋4x－12＝0，解得x1＝2，x2＝－6，所以l2与W围成封闭区域的面积(如图1中阴影所示)为

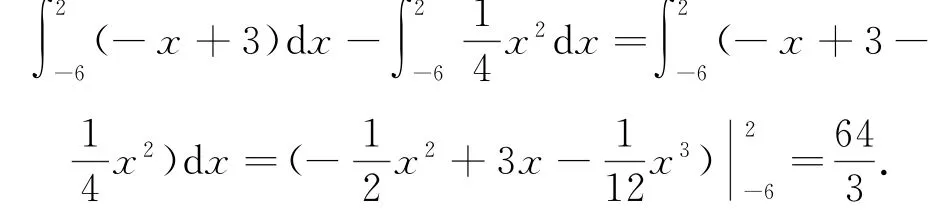
利用定积分的几何意义求曲边图形的面积时，通常先在平面直角坐标系中画出被积函数的图象，再根据图象确定积分的上、下限；最后运用微积分基本定理计算定积分．需要注意的是某些问题若选择x作为积分变量求解较为烦琐时，可以将y作为积分变量进行求解．

2 与概率的交会

例2图2中的曲线是函数x≤π)的图象，在长为2π、宽为2的矩形内，任意投一点，则该点落在阴影内的概率为( )．

图2

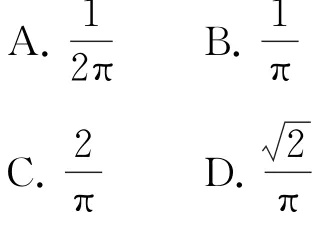
3 与不等式的交会

例3已知x．证明:

(1)当x＞0时，恒有g(x)≥f(x)；

(1)略；

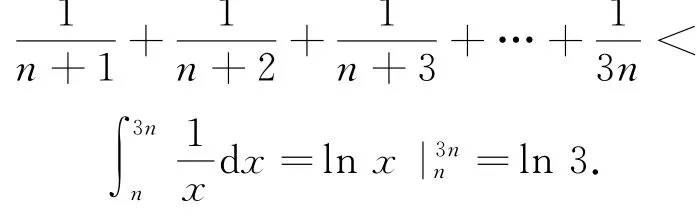
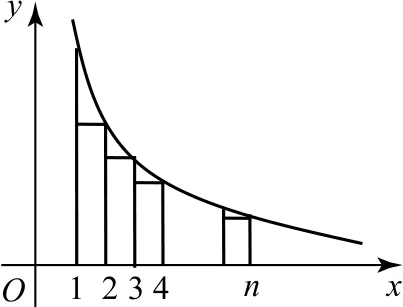
图3

由图4知，区间[n＋1，3n＋1]上的2n个矩形的面积之和大于该区间上的曲边梯形的面积，即

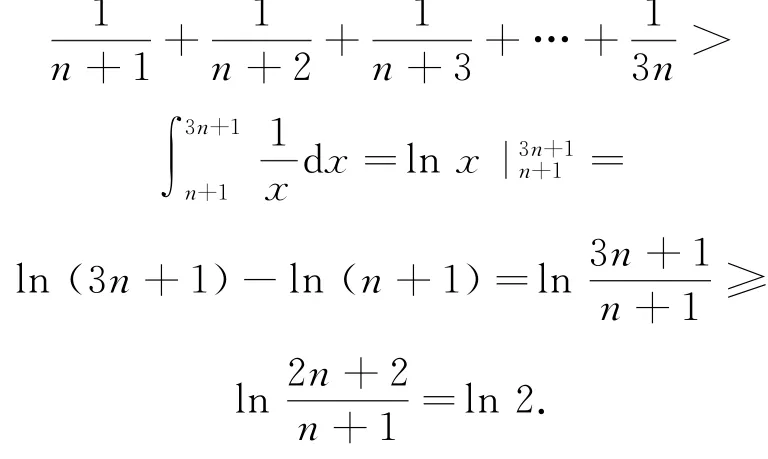
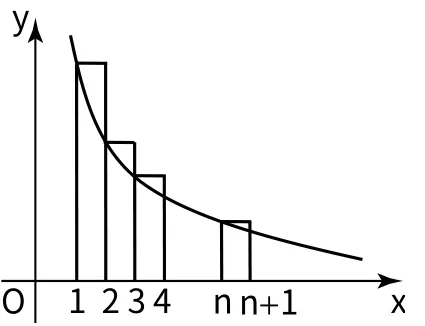
图4

4 与其他学科的交会

例4行驶在平直的高速公路上的一辆汽车，由于遇到紧急情况而刹车，以速度v(t)＝7－3t＋25

1＋t(t的单位:s，v的单位:m·s－1)行驶至停止，在此期间汽车继续行驶的距离(单位:m)是( )．

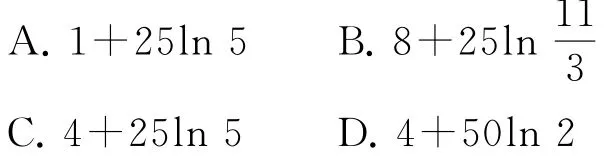
当汽车停止时，v(t)＝0，即0，解得t＝4或(舍去)．所以行驶的距离

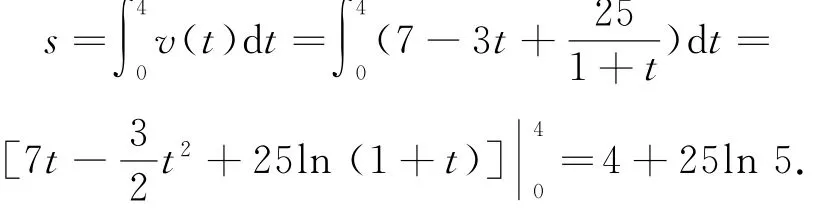
本题与物理中的变速直线运动相结合，考查了定积分的应用．定积分是研究数学、物理等问题的重要工具，它的引入，为解决中学数学、物理中的很多问题提供了简单有效的方法．

除了本文所述的几种典型的交会问题以外，还有定积分与向量、数列等的交会，问题常考常新，但只要我们正确把握定积分的几何意义，准确计算，问题即可顺利获解．