从一道高考题的思路剖析谈高考备考建议

◇ 广东 黄 惠

2020年高考刚刚结束，今年全国卷Ⅰ解析几何大题中第(2)小题考查的主要内容是直线与椭圆的位置关系中的直线过定点问题．直线过定点问题是高考的热点问题，同时也是常规问题，具有一定的综合性，主要考查考生在“动”中找“静”的能力，需要考生具有较强的逻辑推理、数形结合、化归与转化、数据处理等能力．

直线过定点问题的主要求解思路:要证明直线恒过定点，只需证明直线的方程是直线系的形式(含参数)．根据题设，这个参数可以是动点的横坐标，也可以是直线的斜率，所以两种方法本质上是一样的，不同的是选择直线方程的哪种形式问题．

1 高考题的解题思路剖析及引发的思考

例(2020全国卷Ⅰ理科20题)已知A，B分别为椭圆的左、右顶点，G为E的上 顶 点为直线x＝6上的动点，PA与E的另一交点为C，PB与E的另一交点为D．

(1)求E的方程；

(2)证明:直线CD过定点．

1.1 高考题的思路剖析

(2)思路1我们会发现点P是主动点，C，D是点P的从动点，那么C，D的坐标可以用点P的坐标表示出来．根据题意，点C，D分别是直线PA，PB与E的交点，故联立直线与曲线方程即可，这样点C，D的坐标就都跟某个参数有关，即直线CD的点斜式方程只含一个参数(注意要考虑参数的值是否会使斜率不存在的情况出现)，这样就可以找出定点．

解法1由(1)知A(－3，0)，B(3，0)，设P(6，t)，C(x1，y1)，D(x2，y2)，则直线PA的方程为y＝联立方程得

思路2要想证明直线CD恒过定点问题，只需确定直线CD的直线系方程，为了减少参数个数，可设直线CD的方程为y＝kx＋m(斜率不存在时，单独证明)，通过题目已知条件找出k与m的关系．要找出k与m的关系就必须列出关于k，m的等式，通过分析可知等式来源于直线AC，BD相交于点P．

解法2当直线CD斜率不存在时，设直线CD:x＝n，则由(1)知A(－3，0)，B(3，0)，设P(6，t)，由kAC＝kAP得

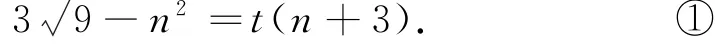
同理，由kDB＝kPB得

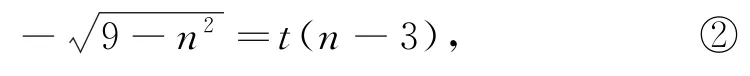
当直线CD斜率存在时，设直线方程为y＝kx＋m，联立方程

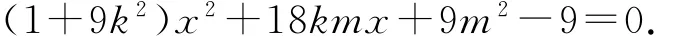
设C(x1，y1)，D(x2，y2)，则

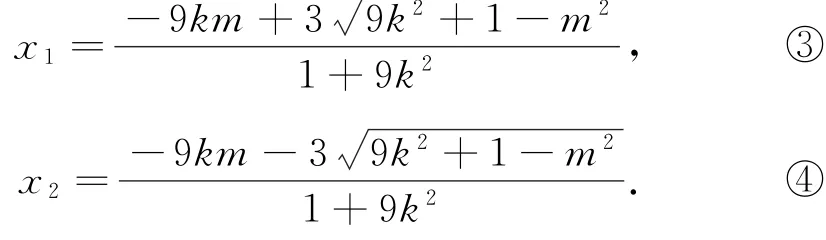
直线AC的方程为把x＝6代入同理，由直线BD得P(6，化简得

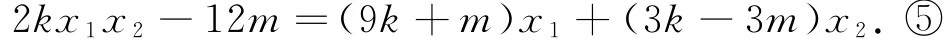
把③④代入⑤，得

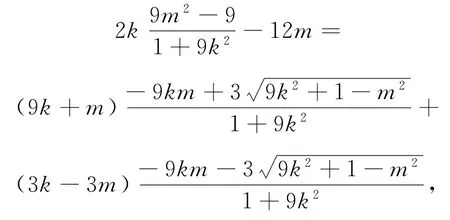
把含有根号的放到等式的一边，整理得

1.2 引发的思考

纵观近几年解析几何大题，不难发现，高考考查的知识点和能力点都没有超出通性通法的范畴，由此引发如下三点．

1)认清解析几何的本质

要引导学生利用代数来研究几何问题，通过几何图形反映代数形式．要关注学生对几何图形的掌握情况，是否会用图形语言来表达几何问题，同时，要关注学生是否会用代数方法来研究几何问题．

有了总体框架之后，立足于学生是否会操作，有没有掌握几何问题“解析化”的过程，从方程、数值、图形中是否能找到几何对象，分析其特征，找到代数的方法，通过代数结果，得出几何结论．

2)重视基本问题

圆锥曲线中最基本的两个问题，一是曲线的定义，二是曲线标准方程的来源．其他问题都是在这两个问题的基础上产生的，所以一定要重视定义的形成过程和方程的推导过程，直线与圆锥曲线的位置关系中常见的模型主要有相交弦长问题、与弦长有关的三角形和四边形问题、定点和定值问题、与向量结合问题等，这些都要有所积累，研究这些问题中的共同特征，掌握基本的解决问题的方法．

3)注重解题策略

解析几何问题考查难度属于中上水平，涉及数形结合、逻辑推理、数学运算等能力，要得出最后结果对学生来说困难重重，所以平时要从这些方面入手:如何引入参数，引入参数的原则是什么(尽量减少参数个数，联系所学的基本模型列出等式，简化运算)；如何设计运算思路，即优化解题过程，关注运算的对象，识别题目所存在的模型有哪些(定点、定值、弦长有关的最值、范围问题等)；如何更接近最后的结果，代数方法的选择(函数与方程思想、设而不求、根与系数的关系、判别式、整体消元等)．虽然题目的问法可能不同，但是掌握一定的策略之后就可以顺利求解．

2 高考备考建议

1)要在理解知识点本质的前提下掌握有关考点

高考试题中，有直接考查知识点简单记忆的试题，但更多的是在对本质理解的基础上对知识应用的考查．例如，“直线方程”部分，从宏观的角度看，其本质是两种转化，即“几何问题代数化”和“代数问题几何化”；从微观角度看，直线方程的5种形式中，“点斜式”的本质是“已知点和斜率就可以确定直线方程”和“已知直线方程的点斜式就可以确定直线的斜率和其经过一点的坐标”．

2)要注重“思路分析”的逻辑性

任何数学问题的解决都要注意两点，首先是思路的切入点，比如本文试题中第(2)题的切入点非常重要；其次是在找到切入点后的分析过程中遇到思维受阻时如何突破的问题．比如今年全国卷Ⅰ的导数应用问题，其切入点非常容易找到，即分离参数，但分离后的函数求最值过程中，针对导函数的最值点判断思维容易受阻，突破的方式就是通过不等式放缩将超越式转化为代数式．

3)要注重“通性通法”

高考试题的解法大多数都在“通性通法”的范畴内，所以在备考中要注重“通性通法”，这样不但可以避免“刷题”的劳累和备考的低效，还会产生“以不变应万变”的自信．

4)要关注“易错点”

高考考查的目标中包括考查“思维的严谨性”，所以在备考中一定要关注每个知识体系或知识块中的“易错点”．