随机游走假设的方差比率检验以及对中国股市管理的启示

●张书君

一、随机游走假设

对于政策制定者和监管从业者来说，信息有效性是衡量股票市场质量的重要指标之一。任何国家的股市都会经历一个从监管、放松监管到再监管的过程。同时，一些学者认为互联网金融、P2P网贷模式和区块链技术的崛起有利于降低并缓解信息不对称的程度。信息不对称是导致股市信息有效性较差的主要原因之一，需要在我国具体的市场环境中进行检验。尤金·法玛的有效市场假说提供了检验这一指标的背景理论。它假设，在一个有效的股市中，任何指数价格或者股票价格都能以一种无偏见的方式，充分、瞬时地反映所有公开可获得的信息。有效市场假说将股市的信息有效性划分为三个层次：弱势有效性、半强势有效性和强势有效性。其中，弱势有效性等同于随机游走假设。也就是说，对于指数或股票价格变化的弱势有效性分析通常伴随着检验其随机游走假设的过程。弱势有效性也意味着该股市至少是有效的，任何指数价格或者股票价格的变化都能以一种无偏见的方式，充分、瞬时地反映所有已知的历史信息。此外，综合判断一个股市是否有效主要取决于该股市中被任意选取的指数或股票价格变化都应符合随机游走的统计学特征。罗和麦金雷于1988 年给出了随机游走假设的递归方程。

股价变化的随机过程包含三种形式的随机游走假设：随机游走 1（Random Walk1：简称 RW1）、随机游走 2（RW2）和随机游走 3（RW3）。RW1 是随机扰动项的独立同分布和同方差性随机游走假设。在RW1 的情况下，εt也被认为是白噪声时间序列和正态随机变量，即εt~i.i.d.N（0，σ02），该序列中的任何非线性函数都是不相关的。RW2 是在RW1 的条件下放松对于εt的同方差性假设以进行自相关，被称为εt的无条件异方差性随机游走假设和独立非同分布假设。RW3 是随机游走假设的最普通形式，被称为εt的有条件异方差性随机游走假设以及既不独立也不同分布假设，仅仅只是连续不相关。很多种方法可以被用来检验有条件异方差性随机游走假设，如ARCH 和GARCH 模型。相比之下，方差比率检验可以用来测试更高层次的随机游走假设，从而有效地区分不同层次的随机性。此外，一些学者在罗—麦金雷方程式的基础上发展出较为成熟与严谨的方差比率检验方法，如Richardson-Smith（1991）、Chow-Denning(1993)和 Kim(2009)。

二、个体方差比率检验

罗和麦金雷的个体方差比率检验主要基于以下事实：当指数或股票价格的收益随着时间的流逝连续不相关时，k 周期（k 天）股票收益的方差应等于k 乘以一个周期（一天）股票收益的方差。周期的指数或股票收益为：

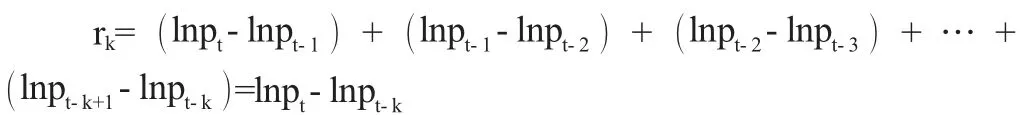
一个周期的收益为：

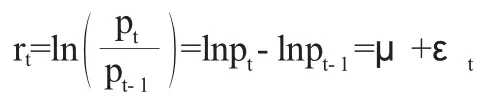
pt和pt-1可以是一个指数或股票在某一天t 以及前一天t-1 的收盘价，μ 是任意的漂移参数，εt是随机扰动项，并且t 的取值在理论上可以从负无穷大-∞到正无穷大+∞。如果μ≠0 而且是常量，则随机过程{lnpt}被认为是带有漂移的随机游走。时间序列lnpt的向上或者向下漂移，主要取决于μ 被标记为正号或者负号。随机过程{lnpt}里的每个lnpt都有自己的概率分布，并且不是相互独立的。

方差比率应大致相当于样本自相关的一个线性组合，k 周期的方差比率为：

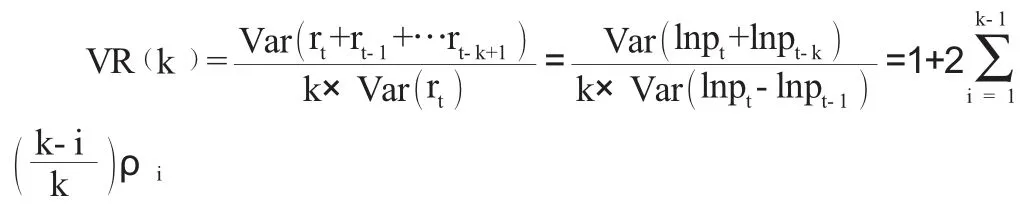
ρi表示股价随时间变化的过程{rt}在滞后i 上的样本自相关系数。方差比率检验的个体零假设（H0）和个体备择假设（H1）分别为：

H0：指数或股票价格的每日回报是随机的，VRφφ k =1；

H1：指数或股票价格的每日回报不是随机的，VRφφ k ≠1。

在上述个体零假设成立的情况下，pi应在所有的滞后上等于零，pi=p2=…=pk=0。同时，k 周期的方差比率也可以被表示为：

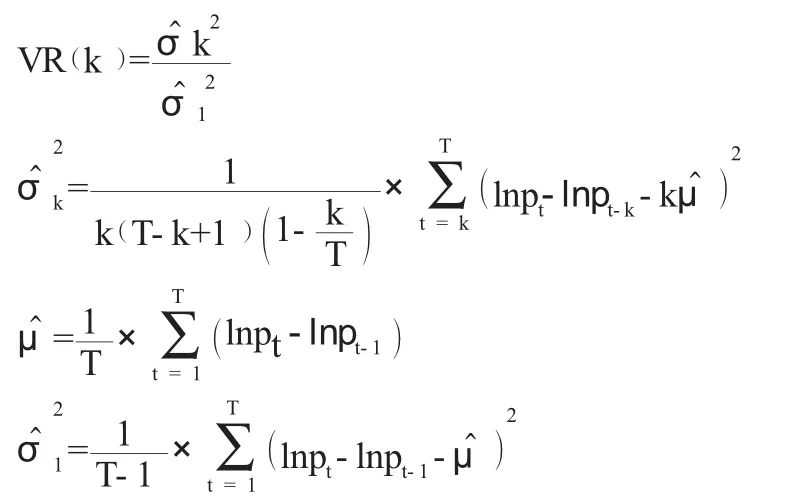
此外，罗和麦金雷于1988 年提出了代表随机游走1（RW1）和随机游走3（RW3）的方程式分别为：Z1（k）和Z2（k）。在εt的独立同分布和同方差性随机游走的假设下，个体零假设的标准化方差比率为：

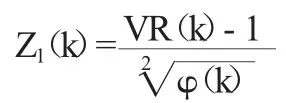
φ（k）是k 周期的渐近方差和独立同分布假设下的方差估计量：

在εt的既不独立也不同分布并且有条件异方差性随机游走的假设下，个体零假设的异方差稳健性检验统计量为：

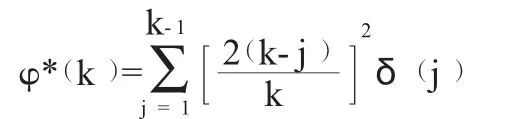
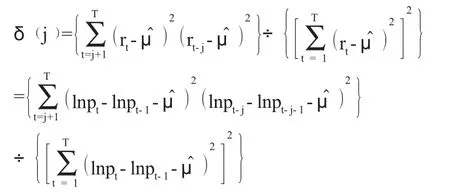
无论Z1（k）是还是Z2（k）的方程式都应渐近地符合标准正态分布，且具有选定的显著性水平5%。在对个体零假设和个体备择假设进行检验时，当k 周期的方差比率值VR（k）接近于1，Z1（k）或者Z2（k）的绝对值小于临界值1.96，并且Z 统计量的概率（p 值）大于5%，接受个体零假设，反之则拒绝。

三、联合方差比率检验

Chow-Denning 的多重比较方差比率检验是在个体方差比率检验的基础上发展而来的，后者仅仅关注单个k 周期下的Z1（k）或Z2（k）。有必要在几个选定的时间间隔内评估和比较一组方差比率统计量。Chow和Denning 于1993 年提出，多重比较方差比率检验能够克服个体方差比率检验的弱点并且可以选择滞后断点k 或者持有期k 的不同值，而不仅仅是单个的k 周期。方差比率检验的联合零假设（H0i）和联合备择假设（H1i）分别为：

H0i：指数或股票价格的每日回报是随机的，VR（ki）=1；

H1i：指数或股票价格的每日回报不是随机的，VR（ki）≠1；

任何 i=1,……l。

可以从Z1（k）或Z2（k）的最大绝对值中获得对于联合零假设和联合备择假设的估计。多重比较方差比率检验是较为保守的方法，为所选的临界值提供了上限1.96。该上限在一个选定的显著性水平上使用渐近的“学生化最大模数”（Studentized Maximum Modulus：简称SMM）分布。从而，用于测试RW1 和RW3 的多重比较方差比率检验的方程式分别为M1和M2。

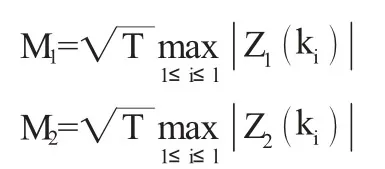
其中，l 是周期k 的样本数量。T 代表自由度和样本大小，理论上取值可趋于无穷大。在对联合零假设和联合备择假设进行检验时，如果Z1（k）或Z2（k）的最大绝对值大于学生化最大模数分布的临界值上限1.96，则在选定的显著性水平上拒绝联合零假设。

此外，Richardson 和Smith 于1991 年提出了另一关于检验同方差性随机游走假设的联合方差比率检验，称为Wald 型检验。

VR 是样本 k 方差比率的 k×1 个向量，1k是 k×1 个单位向量，并且准是VR 的协方差矩阵。Wald 型统计基本符合自由度的渐近卡方分布。原因是每当通过较长的滞后和重叠的观察进行方差比率检验时，其分布都是非正态的。但是，Wald 型检验比Chow-Denning 的多重比较方差比率检验更为强大，但不能在异方差性随机游走假设的情况下进行检验。

另外，Kim 于 2006 年主张使用原始自举法（Wild bootstrap），在计算方差比率之前对数据进行了校正，克服了小样本特性不足、尺寸失真且功耗低等缺点。该方法也是一种无分布随机技术，其中股票的收益被认为是异方差性的并且其分布可以是未知的。

除了计算原始数据外，EViews11 还可以计算秩、秩得分和标记符号等数据类型。但是，赖特的秩检验等方法在检验有条件异方差性随机游走假设时会出现小尺寸失真等缺点。因此，本文主要采用罗—麦金雷、Wald 型检验以及Chow-Denning 的传统检验方法。

四、数据分析结果

为了检验我国内地股市的弱势有效性与随机游走假设，本文选取了上证综合指数与100 家A 股上市公司过去3 年的每日收盘价。通常在T 取值较大、周期k 取值较小的情况下，上述方差比率检验能够更有效地工作。个体检验的k 值被设定为“2、5、10、30”，跨度约为六周。EViews11 的检验结果包含表格和图形两种形式。首先在数据规范栏里选择指数随机游走，检验的是股票每日回报率的对数。选择渐近正太性来计算P 值。取消选中无偏方差和异方差性标准误差选项，只选择去均值数据，目的是为了在无偏差校正的情况下检验独立同分布假设。

图1 是上证综指RW1 的表格检验结果。在个体方差比率检验的结果中，4 个选定周期的方差比率都接近于1，Z 统计量的绝对值都小于1.96，并且用学生化最大模数和较大自由度获得的P 值都大于0.05，从而不拒绝个体零假设。在联合方差比率检验的结果中，Chow-Denning 的最大Z 统计量与周期5 的个体方差比率检验结果相关联，其绝对值0.616074 小于临界值1.96，并且P 值0.9544 大于显著性水平0.05。在Wald 型检验的结果中，虽然Wald 型检验的P 值0.3728 也大于0.05，但是Wald 型统计值4.253069 大于1.96，联合零假设被拒绝。

图2 是上证综指RW1 的图形检验结果。水平轴1.0 代表完全接受个体零假设，即VR（K）=1，也称为零参考线（Null Reference Line）。蓝线是选定周期的实际检验结果，越接近于零参考线，随机性越好。上下两条红线之间的区域是正负渐近标准误差带。当零参考线部分位于正负渐近标准误差带以外时，拒绝个体零假设。从图2 可以看出，蓝线基本接近于零参考线并且零参考线完全位于正负渐近标准误差带以内。

由于上证综指RW1 的联合零假设被拒绝，需要进一步检验RW3。在设置检验独立同分布的基础上，选择异方差性标准误差，并选择Kim 的自举校正法来计算P 值。具体的参数设置如图3 所示，其中Wald 型联合检验法被排除在外，对于随机扰动项εt的同方差性假设也被全面放松。在图3 的表格检验结果中，4个不同周期的个体方差比率值都接近于1，Z 统计量的绝对值都小于1.96，并且它们的P 值都大于0.05，不拒绝个体零假设。Chow-Denning 的最大Z 统计量继续与周期5 的个体方差比率检验结果相关联，其绝对值0.499511 小于1.96，并且P 值0.9380 大于0.05，不拒绝联合零假设。

图4 是上证综指RW3 的图形检验结果。可以看出，实际检验出的蓝线非常接近于零参考线并且零参考线完全位于正负渐近标准误差带以内。相较于图1，图3 中个体周期的方差比率值并没有变化，只是正负渐近标准误差带变大了，最大Z 统计量变小了，P 值也相应地变大了。图4 的随机性比图2 更加完善。上证综指至少已经达到RW3 的水平。

除了检验沪指，本文随机选取了上海、深圳证券交易所各50家上市公司股票自2016 年12 月13 日至2019 年12 月13 日的历史每日收盘价，并检验了它们的随机游走假设。随机选取的股价样本不考虑公司自身的背景和盈利状况，只要是交易所正常上市的、符合数据要求的即可。总共100 只股票的大样本数据保证了此次检验的真实性和可靠性。在随机选取的上交所50 只股票中，14%（7 只）达到了 RW1，80%（40 只）达到了 RW3，20%（10只）达不到RW3。在随机选取的深交所50 只股票中，16%（8 只）达到了 RW1，84%（42 只）达到了 RW3，16%（8 只）达不到 RW3。

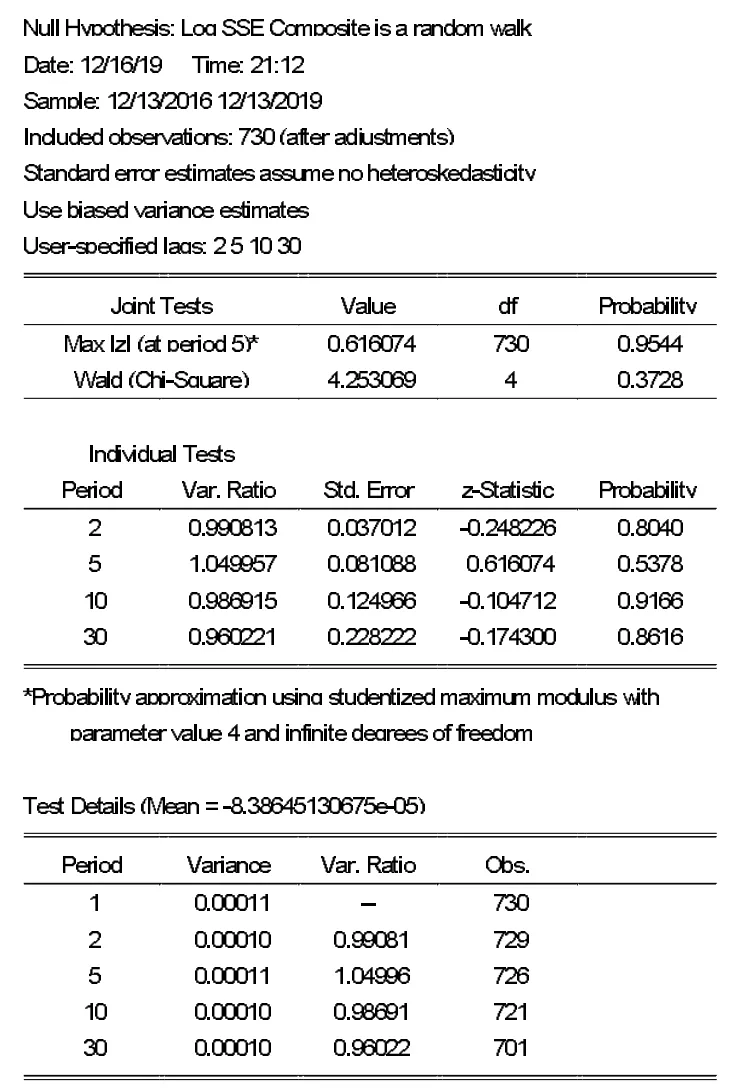
图1 上证综合指数随机游走1 的表格检验结果

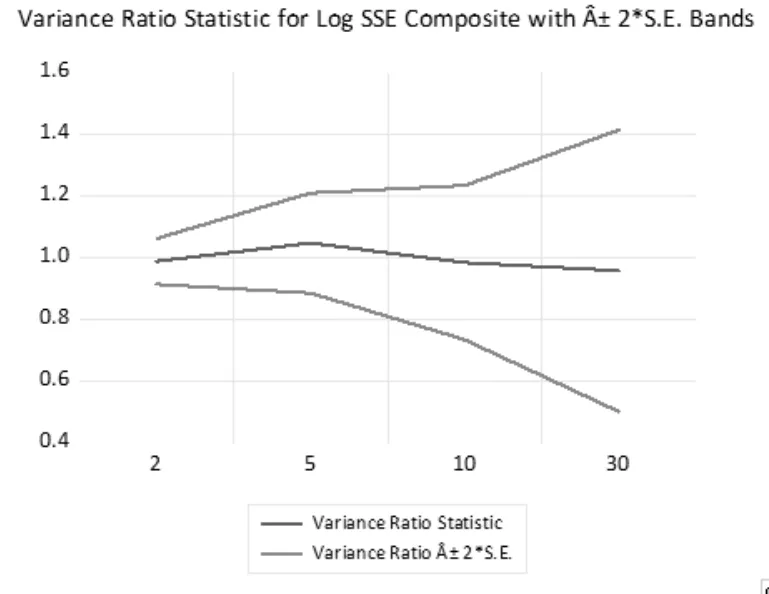
图2 上证综合指数随机游走1 的图形检验结果

通过以上的检验结果得知，上海和深圳两大证券交易所之间没有显著的差距，有效和无效的股票占比大致相当。尽管如此，同方差性随机游走假设本身是一种比较严格的检验方法，总计85 只股票被Wald 型检验的联合零假设拒绝，49 只股票由于被Wald 型联合零假设拒绝而没能达到RW1。与此同时，A 股市场上的股票质量存在两极分化的现象，总计15 只股票达到了RW1，而另外18只股票达不到RW3。

总之，我国内地股市目前达不到弱势有效性的水平，还没到放松监管的时候。股市的管理应当是一个动态的过程：当有效性水平被证明较低时，需要强监管；当绝大多数参与者都能够遵守规则且自律时，应当还给市场一定的自由度。即便是已经被证明为有效的上市公司股票，依然有进一步提升质量的空间（从RW3 提升到RW1）。证监会、交易所和行业内自律组织可以参考该检验结果开展股票质量的评级。在这方面，上证综合指数反而被证明了是能够代表我国内地股票质量的中间水平，但无法反映两极分化的现象。

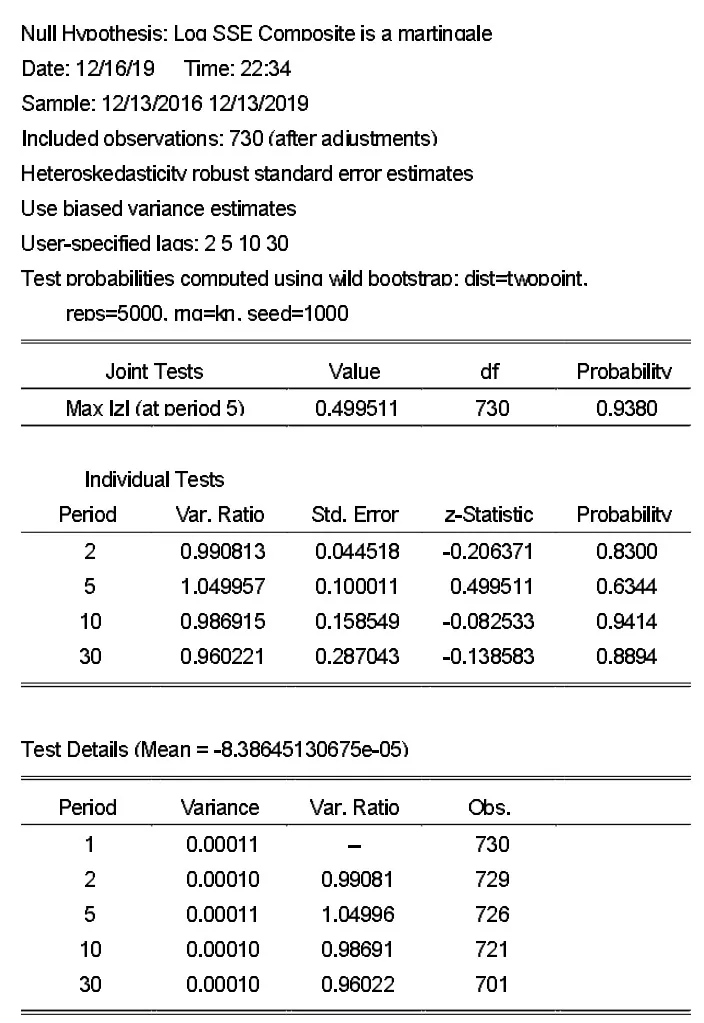
图3 上证综合指数随机游走3 的表格检验结果

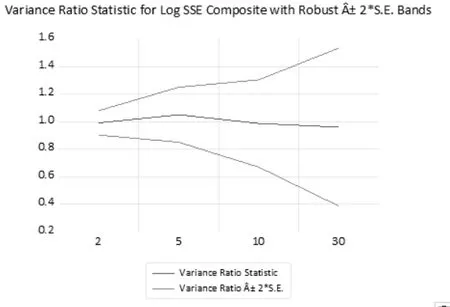
图4 上证综合指数随机游走3 的图形检验结果

此外，互联网金融已发展了多年，并没有从根本上解决信息不对称的问题。P2P 网贷平台主要针对的是民间小额借贷，对于传统交易所平台的股权转让难以形成实质性的影响力, 更何况P2P 网贷平台自身也存在信息不对称等问题。区块链概念的崛起带给中国股市未来很大的想象空间，但技术和平台尚不完善。因此，在积极探索新技术应用的同时，有必要继续加强传统交易所体系下的金融监管，尽量弥补在这一领域与西方发达国家之间的差距。