柱塞式调节阀壁面粗糙度对流量系数影响的 数值模拟研究
2020-10-14王洪申张家振
王洪申,张家振,陈 杰
(1.兰州理工大学 机电工程学院,兰州 730050;2 浙江维都利阀门制造有限公司,浙江温州 325024)
0 引言
流量特性和流量特性曲线是评估调节阀性能的重要指标,整个设计过程中应该依存的基本参数的流量系数[2],因此,准确测量流量系数非常重要。影响阀门流量系数的因素有很多,阀门结构的改变、空化现象、壁面粗糙度等都能对流量系数产生影响,国内外学者已经通过计算流体力学(CFD)的方法对此做了大量的工作。
Chern 等[3]通过在截止阀的阀座之上加一个多孔保持架,可以有效地降低空化对阀门的破坏;Palau-Salvador 等[4]通过改变阀座的形状,优化了控制阀的流动性能,减小了涡流区域,降低空化效应,提高了流量系数,从而提高阀门的工作性能;李根飞等[5]研究了在不同的压差下,调节阀的流量系数随开度的变化规律,结果表明,在同一个开度下,流量系数随压差的增大而增大,但增长幅度很小,在同一个压差下,流量系数随开度的增大而增大,且成等百分比关系;蔡标华[6]研究了扇环形窗口、椭圆形窗口和V 型窗口3 种不同形状的窗口对套筒调节阀调控特性的影响,结果表明,窗口的几何形状对流量系数影响很大,扇环形窗口和椭圆形窗口对应近似线性流动特性,而V 型窗口对应等百分比流动特性;陈云富等[7]运用混合两相流模型和完全空化模型对喷油器内部的空化流动特性进行数值模拟研究,并研究了壁面粗糙度对喷油器内部空化流动特性的影响,结果表明,流量系数随粗糙度增加而减小,流量系数随空化参数的增加而缓慢增加;Sun 等[2]研究了粗糙度对三偏心蝶阀流量系数的影响,做了不同开度和粗糙度下的对比试验,结果发现,在开度一定时,随着粗糙度的增大,流量系数减小,模拟结果与试验结果在大开度时吻合度较好,在小开度时吻合度不好。
以上研究工作主要针对阀门结构的改变和空化现象的发生对阀门流量系数进行分析,但是关于粗糙度对流量系数影响的研究较少,而粗糙度是影响阀门流动性能的一个重要因素,研究价值明显。本文针对DN50柱塞式调节阀(如图1所示)设置了100,200,300 μm 3 种粗糙度,采用数值模拟与试验验证相结合的方式,研究在不同开度情况下不同粗糙度对流量系数的影响。
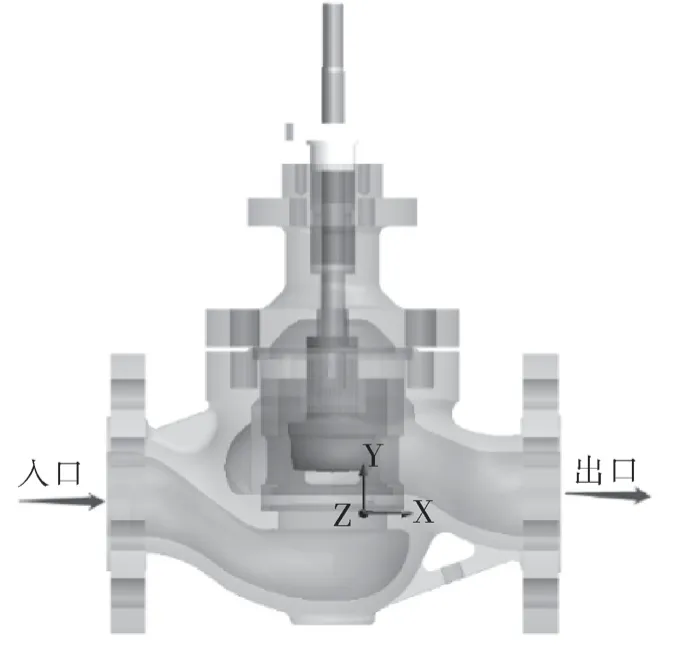
图1 DN50 柱塞式调节阀
1 数学模型
1.1 控制方程
由于调节阀内部三维流动是不可压缩的黏性流动,物理守恒定律是流体流动的基础,对流体流动而言,基本控制方程主要由伯努利方程、连续性方程和Navier-Stokes 方程组成[8-9]。
(1)伯努利方程
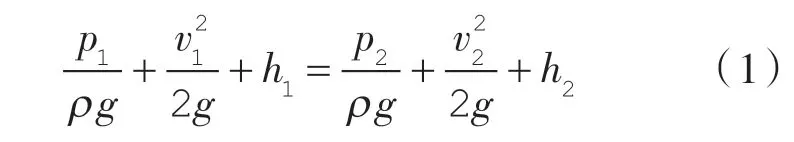
式中 p1,p2——微元体在某一点所受的压力;
ρ ——密度;
v1,v2——微元体在某一点的速度;
h1,h2——微元体在某一点的高度。
(2)连续性方程
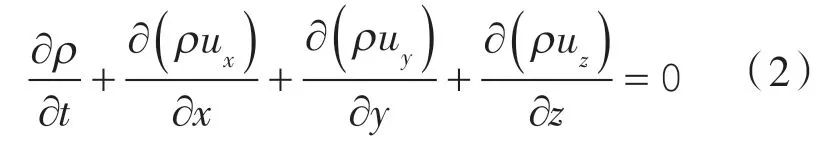
式中 ux,uy,uz——x,y,z 方向上的平均速度;
t ——时间。
(3)Navier-Stokes 方程(动量守恒方程)
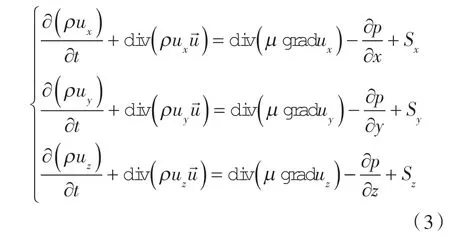
式中 gradui—— 流体的动力黏度系数;
p ——平均静压;
Sx,Sy,Sz——动量守恒方程的广义源项。
1.2 流量特性
柱塞式调节阀的固有流量特性根据阀芯结构的不同分为直线流量特性、快开流量特性、等百分比流量特性和抛物线流量特性。如图2 所示,根据调节阀阀芯的截面形状可以看出,该调节阀符合等百分比流量特性。

图2 调节阀阀芯的截面形状
等百分比流量特性是指通过阀门的相对流量与相对开度成正比例关系,有如下关系式:
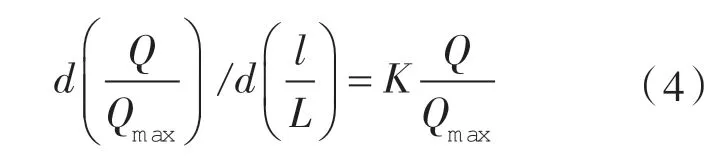
式中 Qmax——阀门流经的最大流量;
L ——阀门的最大开度。
设可调比R=Qmax/Qmin,Qmin为阀门的最小流量,Qmin通常是Qmax的1%~3%。
将式(4)进行积分,得到:
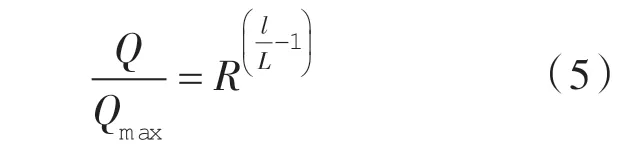
将l=0,Q=Qmin;l=L,Q=Qmax,R=50 代 入 式(5)得到:
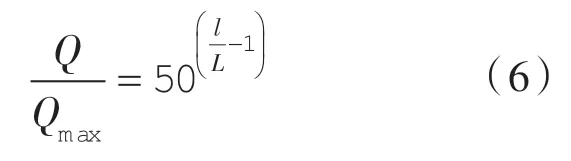
1.3 粗糙度模型
无论用何种加工方式,产品表面都会有微观不平度,这些不平度用粗糙度来表达。轮廓算数平均误差Ra 是评定表面粗糙度的重要参数,是指在某一段取样长度内,轮廓上的点到基准线之间距离的算数平均值,也可以用积分形式表示。
轮廓算数平均误差Ra:
积分形式为:
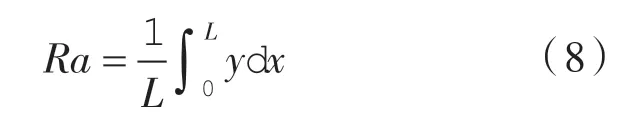
壁面粗糙度的影响可以使用Pattanapol 等[10]提出的“修改后的壁面定律”对粗糙度进行建模,对壁面的修改定律定义为:
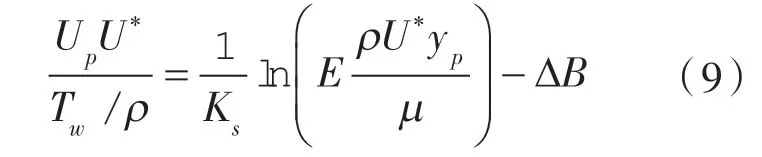
式中 Up——介质流动时的平行分速度;
Tw——壁面剪切力;
Ks——经验常数,Ks=0.41;
E ——经验常数,E =9.793;
yp—— 粗糙度顶点与邻近单元中心点的 距离;
μ ——动力黏度;
Cμ——经验常数,Cμ=0.09。
ΔB 归于粗糙度效应的指数定律中的偏移,其大小取决于量纲粗糙高度Ra+。
当Ra+≤2.25 时,ΔB=0;
当2.25<Ra+≤90 时,
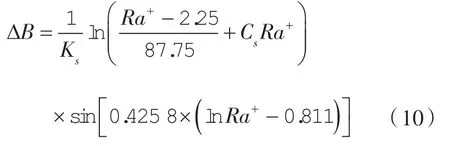
当Ra+>90 时,
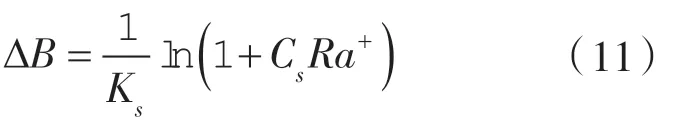
式中 Cs——粗糙度常数;
Ra —— 轮廓算数平均误差,也叫粗糙高度。
2 数值模拟
2.1 理论曲线
2.1.1 流量系数
国际上规定阀门的流量系数是5~40 ℃温度范围内的水流经阀门,两端压差为100 kPa 时,以m3/h 为单位的流量数值[10],表示符号是Kv,根据式(12)进行计算:
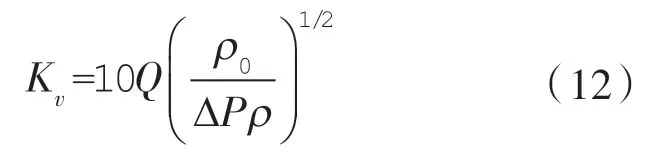
式中 Q ——阀门的流量,m3/h;
ρ0——水在15 ℃时的密度,通常ρ/ρ0=1;
ΔP ——阀门两端的压差,kPa。
所以,流量系数公式一般写成如下的形式:
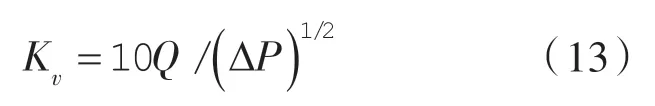
流量系数也可以用美标符号Cv表示,Kv和Cv的关系是:

2.1.2 理论曲线

对应的流量系数见表1。

表1 流量系数
2.2 数值模拟
2.2.1 网格设置
首先在SolidWorks 中构建出阀门的三维模型,根据标准GB/T 30832-2014 阀门 流量系数和流阻系数试验方法[10]中的规定,在阀门的进口端加2D 长的管道,在阀门的出口端加6D 长的管道,添加完管道后的模型如图3 所示。
图3 阀门的分析模型
建模之后,将模型导入Ansys Workbench 中,首先抽取整个流道,利用Mesh 模块划分网格。由于四面体网格具有快速生成、自动细化、精确度高的优点,所以选择生成四面体网格,生成的网格如图4 所示,一共生成1 215 453 个网格,229 144个节点,在曲面上曲率大的地方网格密集,在曲率小的地方网格稀疏,这样既能保证分析的准确性,又能提高分析效率。
图4 模型网格生成
2.2.2 求解与分析
用FLUENT 模块进行阀门的流体仿真,计算模型选择RNS k-ε湍流模型,选择30 ℃的水作为流动介质;选择压力作为进出口边界条件,其中进口压力200 kPa,出口压力100 kPa;压力速度耦合算法采用SIMPLE 算法,压力插值方式采用二阶插值方式,单元中心的变量梯度选择Least Squares Cell Based,其他项采用二阶迎风插值,适当调节松弛因子直到收敛。一共做4 组仿真试验,依次设置壁面粗糙高度为0,100,200 和300 μm,在11 种开度情况下,测量入口的体积流量Q,并作出相对开度—流量系数曲线。
如表2~5 所示,在同一开度时,随着粗糙度的增加,流量系数有一定程度的减少,为了更好地表现出每增加一级粗糙度,流量系数减少的比例,做出流量系数随粗糙度变化比例见表6。

表2 无粗糙度流量系数变化

表3 100 μm 粗糙高度流量系数变化

表4 200 μm 粗糙高度流量系数变化

表5 300 μm 粗糙高度流量系数变化
由表6 可知,在开度一定时,随着粗糙度的增加,流量系数值比上一级粗糙度的都有减小,减小的程度不同,其中在小开度和大开度时,随着粗糙度的增大,流量系数变化量较大。若是规定每一级的变化量不超过1%,调节效果比较好,从表6可以看出,相对开度在0.5~0.8 范围内,粗糙度对流量系数的影响不大,故当考虑粗糙度影响时,12.5~20 mm 开度是理想开度。

表6 流量系数随粗糙度变化比例
2.3 模拟结果与理论曲线验证
由于流量特性曲线是阀门在理想状态下的流量系数曲线,没有考虑摩擦的存在,所以用流量特性曲线来验证粗糙高度为0 μm 时的模拟数据的准确性。
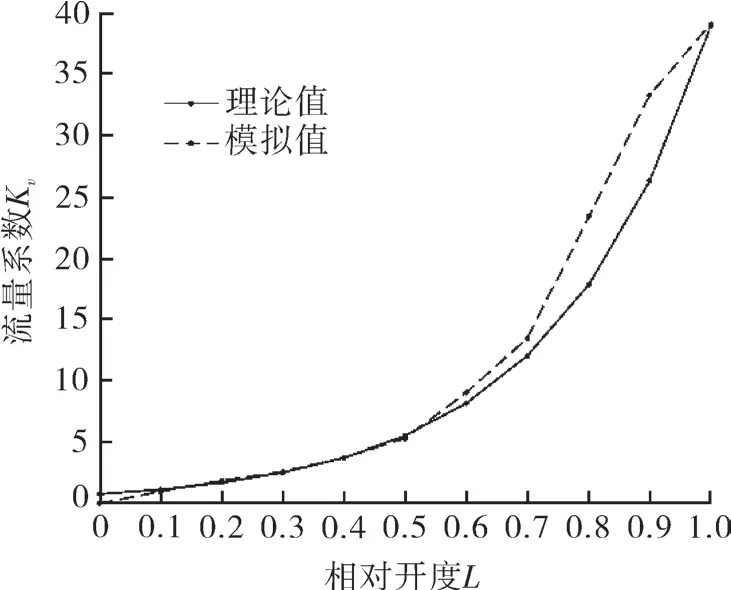
图5 理论曲线与模拟曲线对比
如图5 所示,模拟曲线的趋势大致符合等百分比流量特性趋势,在相对开度为0~0.7 时吻合度比较好,相对开度大于0.7 时,模拟数值要大于理论值,具体原因是当开度大于70%时,出口流量快速增加,导致曲线斜率变大,而后在相对开度达到0.9 时,流量增长变慢,从而在全开状态下,理论值与模拟值吻合。总体来看,模拟结果与理论曲线的趋势相同,符合等百分比流量特性曲线,模拟结果与理论曲线是吻合的。
3 试验验证
3.1 试验装置与试验方法
采用如图6 所示的试验原理,对阀门进行流量系数的测试试验。在试验开始,开启齿轮泵,齿轮泵将介质输送到压力调节阀,调节阀门,使得压力测量仪所测量的入口压力为一定值,同样,调节阀门,使得压力测量仪所测量的出口压力为一定值,待流量稳定后,读取流量计测得的流量。
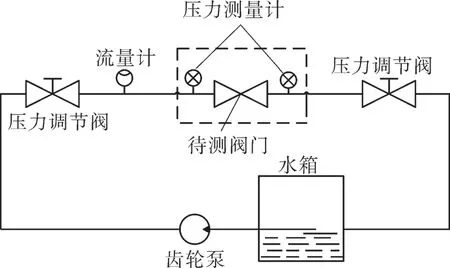
图6 阀门试验的原理
为了减小因测量和不稳定流动导致的误差,在每一个开度下,分别由3 个不同的净压差测3组数值,而后取平均数。即取相对开度分别为0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0,在每一个开度下,分别使净压差为0.08,0.1,0.12 MPa,在每个净压差下测量流量,进而求得流量系数,最后取算数平均值,试验结果如表7 所示。

表7 试验结果
3.2 数值分析与试验方法验证
将Ansys FLUENT 软件分析结果与试验结果作对比,如图7 所示。发现在小开度和大开度时,模拟结果与试验结果有一定的差异。在相对开度小于0.6 时,试验值要比模拟值大,这是因为在数值模拟没有考虑到阀门小开口流动的实际物理条件,软件在处理介质流动时,有一定的冗余壁面,因此在小开度时,介质实际流过量比模拟流过量要大;在相对开度大于0.6 时,试验值要比模拟值低,那是因为随着开度的增大,流量变大,真实介质流动过程中会受到重力、旋涡等不稳定因素的影响,所以结果会略小于模拟值,故在考虑介质实际流动情况下,数值模拟结果与试验结果基本 吻合。
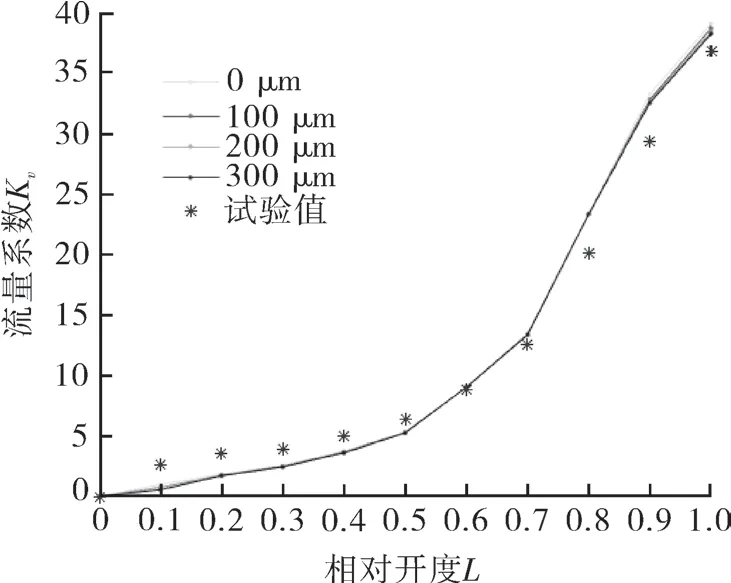
图7 数值模拟与试验验证的对比
4 结论
(1)用CFD 软件对流量系数进行数值模拟,随着开度的增加,流量系数增大,且符合等百分比流量特性。
(2)用CFD 软件对流量系数进行数值模拟,可以发现,当开度一定时,增大壁面的粗糙高度,流量系数有不同程度的减小。其中相对开度在0~0.4 和0.9~1 时,流量系数随粗糙度变化量大,在相对开度为0.5~0.8 时,粗糙度对流量系数的影响不大,故当考虑粗糙度影响时,12.5~20 mm 开度是理想开度。
(3)比较无粗糙度时的数值模拟结果与理论结果,发现在相对开度为0~0.7 时,模拟结果与理论曲线吻合度最高,在大开度时,模拟值比理论值大,在误差允许范围内,整体上与理论曲线吻合。
(4)比较数值模拟结果与试验结果,发现在相对开度为0~0.6 时,试验值要比模拟值略大,在相对开度大于0.6 时,试验值要比模拟值略小,在考虑介质实际流动情况下,数值模拟结果与试验结果基本吻合。
