变截面无油涡旋压缩机轴向间隙泄漏模型的研究

2020-10-14王建吉胡天林

流体机械 2020年9期

关键词：型线涡旋径向

王建吉，刘涛，胡天林

（1.陇东学院机械工程学院，甘肃庆阳 745000；2.兰州理工大学机电工程学院，兰州 730050）

符号说明：

a ——基圆半径；

φ ——涡旋型线展开角；

C0，C1，C2，C3——待定系数；

φ1，φ2——型线接合点展角；

t ——齿厚；

Rt（φ22）——A 点的切向向量；

φ22——B 点的切向角；

Rn（φ22）——A 点的法向向量；

φ11——A 点的切向角；

Ror——回转半径；

（x0，y0）——A 点的坐标；

θx——修正开始主轴转角；

θ*——开始排气角；

θ ——主轴转角；

γ ——型线修正角；

λ——修正圆弧中心角；

α ——渐开线起始角；

μ——黏度；

v ——气体泄漏速度；

m——质量泄漏率；

ρ ——泄漏气体密度；

A ——泄漏出口横截面积；

L（θ）——第θ腔瞬时径向泄漏线长度；

φa——瞬时径向泄漏线初始展角；

φb——瞬时径向泄漏线终止展角；

R ——气体常数；

Vi—— i 工作腔容积；

pi——i 工作腔气体力；

Ti——i 工作腔温度；

ps——吸气压力；

Ts——吸气温度；

κ ——等熵指数；

δa——轴向间隙。

0 引言

无油涡旋压缩机具有结构简单、体积小、效率高等特点，广泛应用于食品加工、医疗等领域。但在使用过程中仍然存在许多技术问题，如涡旋盘加工精度、间隙泄漏等制约涡旋压缩机在大功率工况下的应用。涡旋压缩机的泄漏分为径向间隙泄漏和轴向间隙泄漏。通过径向间隙的切向泄漏虽然存在，但由于以下两方面的原因，对整机泄漏影响较小。一方面，可通过提高涡旋盘加工精度减小安装间隙以减小切向泄漏。另一方面，经径向间隙的切向泄漏线较短，产生的泄漏量较小。控制涡旋压缩机的轴向间隙所产生的径向泄漏是一项技术难题，径向泄漏使得高压腔介质通过轴向间隙泄漏至低压腔和吸气腔，造成介质重复压缩，降低了涡旋压缩机工作效率。

变截面涡旋齿和等截面齿相比较，减少涡旋圈数，可实现大的压缩比。更重要的是减少了轴向间隙泄漏线的长度，提高的容积效率。Liu 等［1］利用等距曲线法建立圆弧和圆弧渐开线组成的变截面涡旋齿，并与等截面进行仿真比较。得出容积比和泄漏损失均由于等截面齿。彭斌等［2-3］给出了变截面涡旋型线在某一瞬时泄漏线的计算方法。并运用改进的Euler 法对所建的泄漏模型进行求解，得到有无泄漏2 种工况下的温度、压力和质量的变化。该研究主要分析泄漏对各工作场和质量的影响程度，没有给出间隙泄漏准确的计算模型。查海滨等［4］运用CFD 得到变截面涡旋压缩机不同压差、不同间隙宽度的径向泄漏和切向泄漏质量流率，该模型仅对于稳态模型展开研究。Sun 等［5］利用CFD 实现间隙泄漏的可视化，并研究了变截面涡旋压缩机泄漏流动机理，但忽略了气体黏性对泄漏的影响。

为了研究介质泄漏对整机效率的影响和泄漏量在工作过程中的变化规律，建立准确的泄漏计算模型是必不可少的。陈荣等［6-7］利用范诺流理论建立了微型涡旋压缩机间隙的泄漏模型，确定了合理的泄漏间隙的范围，但该模型仅针对等截面涡旋盘，也没有考虑涡旋齿几何参数对泄漏的影响。Chen 等［8］给出了径向和切向泄漏面积的计算方法，没有给出完整的泄漏量计算方法。Ishii 等［9］建立了间隙泄漏的流动方程，并通过试验进行了验证，然而在该计算模型中没有考虑温度的影响。刘兴旺等［10］利用宏观能量法和黏性流动理论建立了涡旋齿迷宫密封泄漏量的计算模型，并通过试验进行了验证，该模型只针对有迷宫密封的结构，对无密封和其它密封具有参考意义。

为了准确分析涡旋压缩机各工作腔的泄漏特性，本文以整机为研究对象，分析变截面无油涡旋压缩机在任一瞬时工作腔的径向泄漏情况，以圆渐开线、高次曲线和连接圆弧组成的变截面涡旋齿为例，分析泄漏率与泄漏线长度、涡旋齿齿厚、工作腔容积、腔体温度之间的数值关系，建立变截面涡旋压缩机在任意主轴转角时径向泄漏量的计算模型，通过求解该模型，得出基圆半径、泄漏间隙对泄漏量影响的变化规律，并通过仿真模拟对计算模型进行验证，可为新型线涡旋盘的加工、装配和密封提供理论参考。

1 变截面涡旋型线泄漏线长度

1.1 型线方程

选择圆渐开线、高次曲线、连接圆弧组成的变截面涡旋型线为例，母线的数学表达式如下。

第1 段为基圆渐开线，方程为：

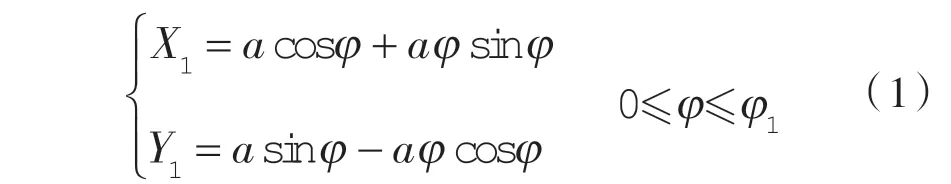
第2 段为高次曲线，方程为：

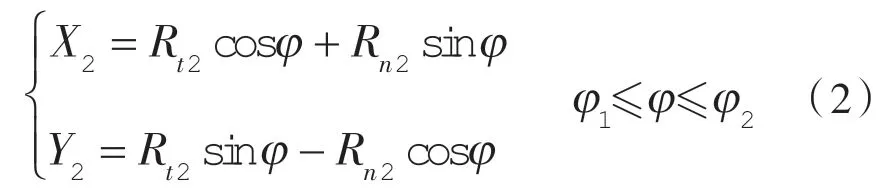
在确定参数a，φ1，φ2后，根据接合点处的约束条件得到位置参数值，带入型线方程得到变截面涡旋型线的母线方程，利用法向等距法可以得到动、静涡旋齿外壁型线然后利用双圆弧修正法，对涡旋齿齿头进行修正。涡旋齿几何模型和径向泄漏截面如图1 所示。

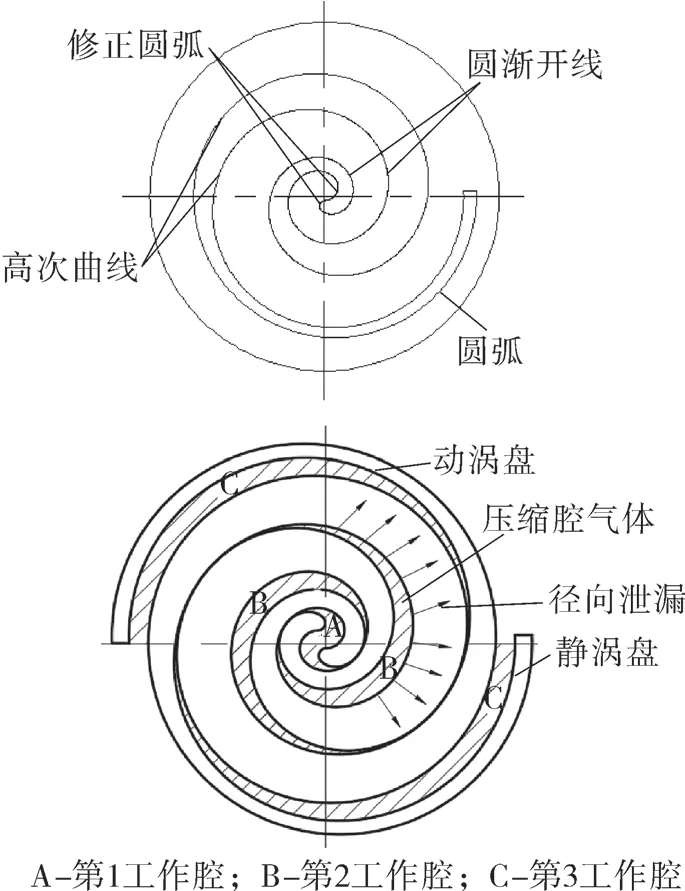
图1 涡旋齿几何模型和径向泄漏截面

1.2 涡旋齿壁厚

涡旋齿齿厚大小会对径向泄漏大小产生影响，而变截面涡旋齿齿厚随涡旋齿展角发生变化，因此研究齿厚的变化规律很有必要，根据涡旋盘几何关系和图2 所示的齿厚计算示意，可以得出齿厚与展角的函数关系［11］。

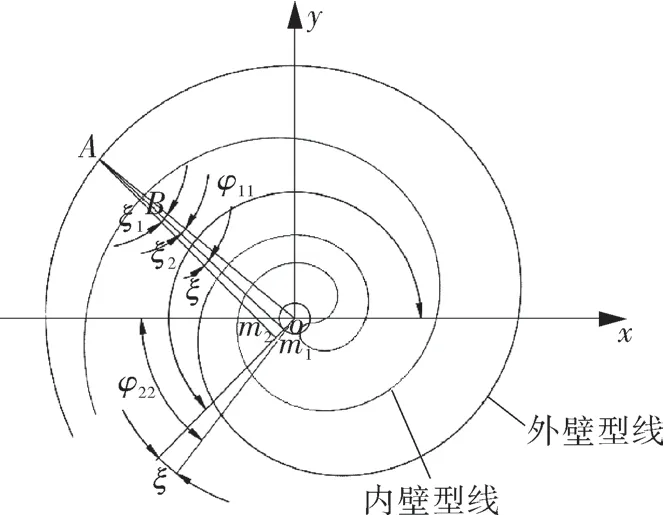
图2 齿厚计算示意

根据几何关系可知齿厚：

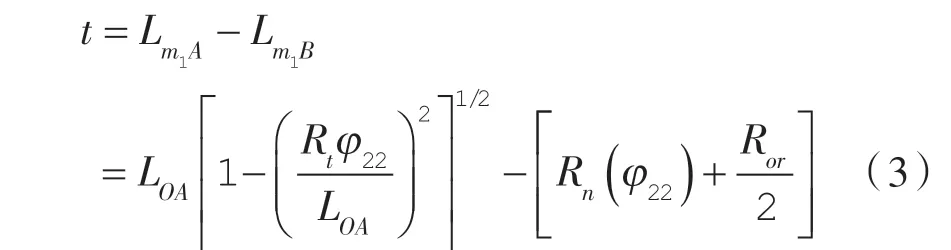
1.3 泄漏线长度

以第2 工作腔为研究对象，径向泄漏线包括第1 工作腔流入第2 工作腔泄漏线和第2 工作腔泄漏到第3 工作腔泄漏线。涡旋压缩机在正常工作时，吸气、压缩、排气过程同时进行，在每一主轴转角时泄漏线长度均会发生变化。

（1）当0 ＜θ≤θx时，

第1 腔径向泄漏线：

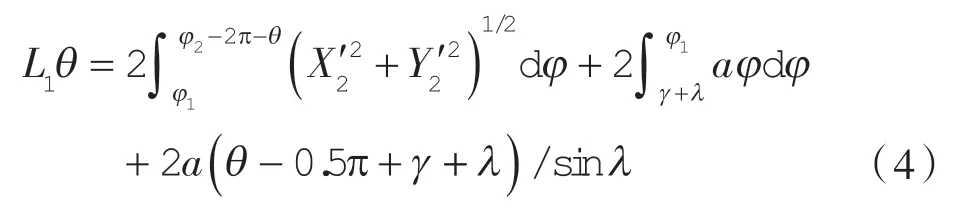
第1 腔容积表达式：

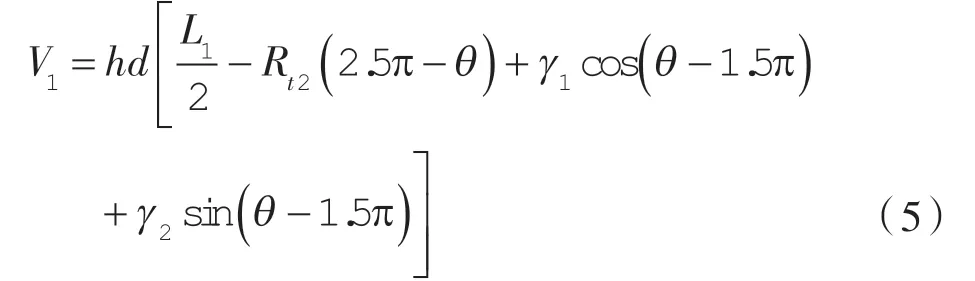
其中

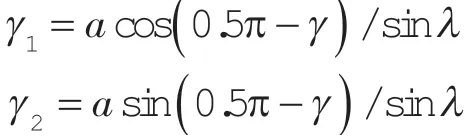
第2 腔径向泄漏线长度表达式：

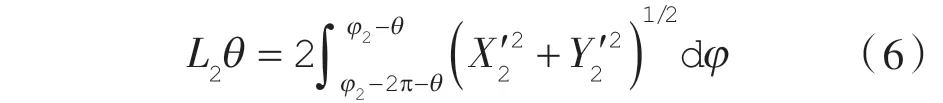
第2 腔容积表达式：

（2）当θx＜θ≤θ*时，

第1 工作腔径向泄漏线：

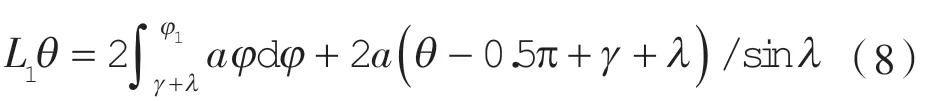
第1 工作腔容积表达式：

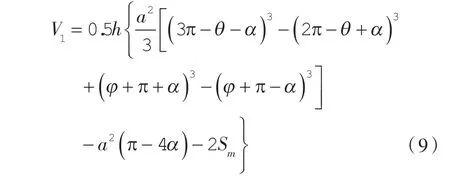
第2 工作腔径向泄漏线：

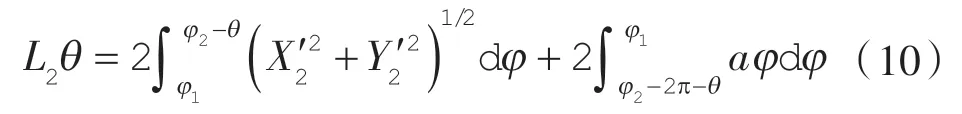
第2 工作腔容积表达式：

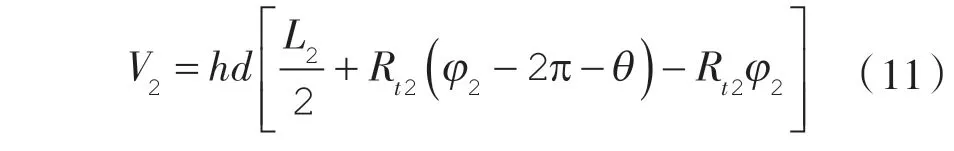
（3）当 θ*≤θ≤2π 时，

第1 工作腔径向泄漏线：

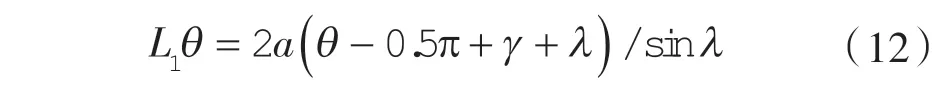
第1 工作腔容积表达式：

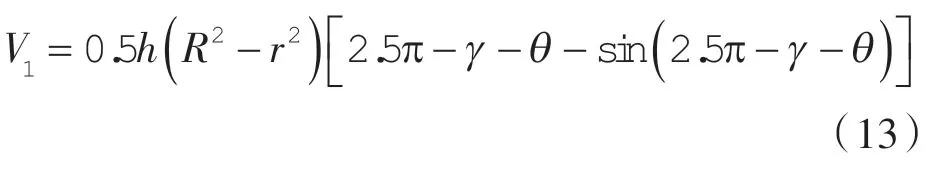
第2 工作腔径向泄漏线：

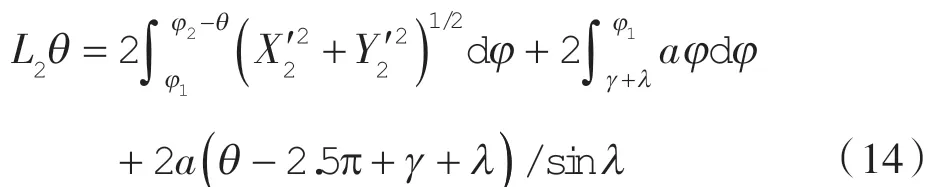
第2 工作腔容积表达式：

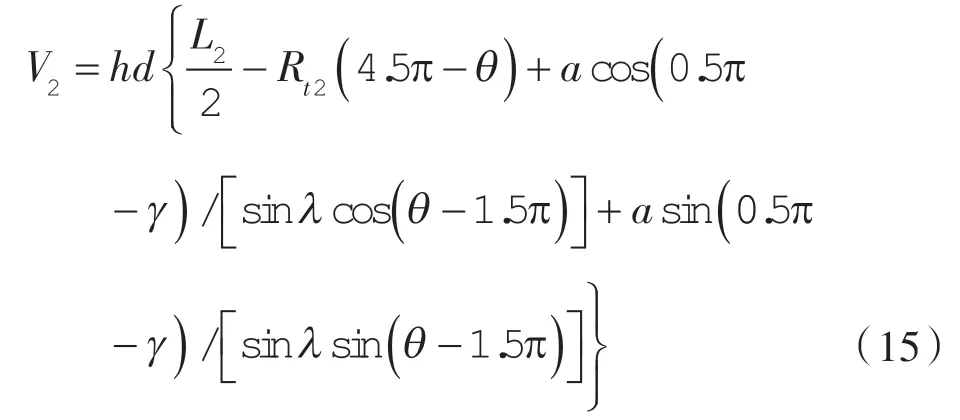
（4）吸气腔容积

该段基线长度表达式：

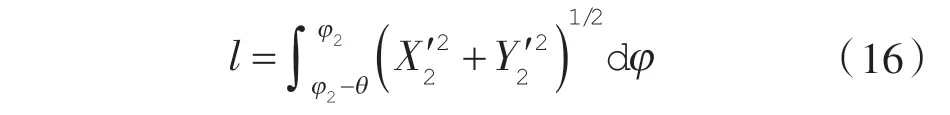
吸气腔容积表达式：

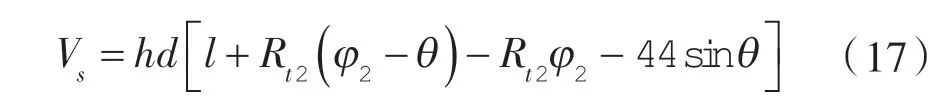
2 泄漏量计算模型

涡旋压缩机回转半径小、线速度较小，泄漏气体可假设为理想气体，其温度变化近似看做线性变化，认为气体在泄漏间隙中的流动视为等熵层流流动。沿泄漏方向取泄漏线微段dL 为研究对象，微段的流动模型如图3 所示［11］。

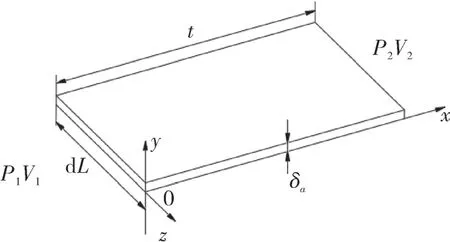
图3 轴向间隙泄漏等效模型

（1）运动微分方程

假设间隙内气体为一维绝热流动，则运动方程式为：

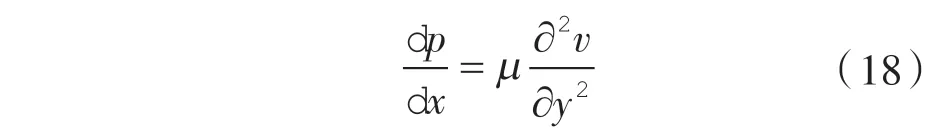
当y=0 时，v=0；y=δa时，v=0。

（2）连续方程

一维定常可压缩流体的连续方程为：

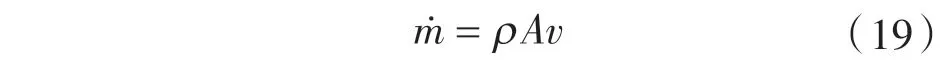
（3）状态方程

根据理想气体状态方程：

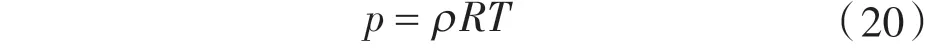
对方程（18）关于y 进行积分可得截面速度表达式：

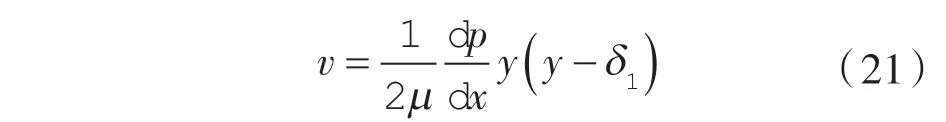
间隙内气体平均速度为：

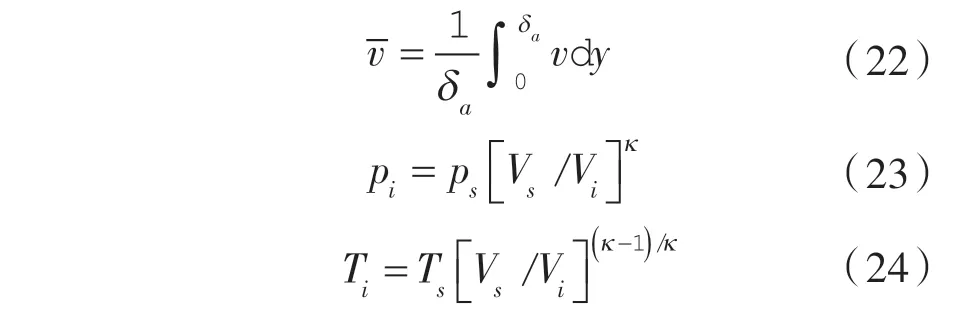
将式（20）～（24）代入到式（19）中得到任意工作腔在主轴转角时的径向平均质量流量表达式：

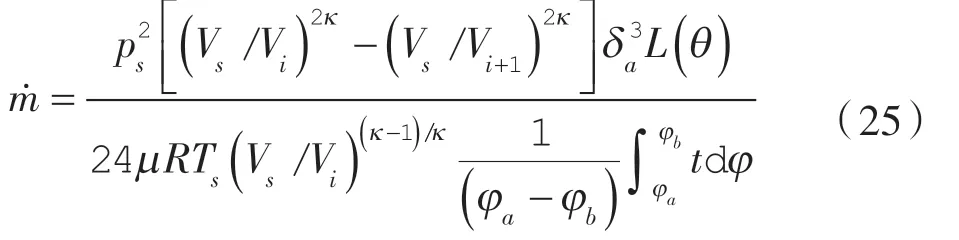
3 泄漏模拟计算

为了验证间隙泄漏流量计算模型的准确性，利用FLUENT 软件模拟涡旋压缩机在工作过程中的泄漏，将模拟结果与数值计算结果进行对比。模拟样机的基本参数见表1，对涡旋盘转动一周过程中第2 工作腔泄漏气体速度和泄漏气体密度进行追踪。图4 示出吸气结束时刻流场分析结果。从图4（a）可看出，压缩腔内气体压力从外向内逐渐增大，在动静涡旋盘啮合间隙处压力有突变现象，这是由于在间隙处，气体被挤压，密度发生变化所造成；从图4（b）的温度分布可看出，对称的2 个月牙腔体温度分布相似，并且温度随着啮合间隙的减小而增大，最小间隙处出现极值，这是因为随着啮合间隙的减小，气体受挤压后，除了气体分子之间的摩擦外，动静旋盘之间也可能接触发生摩擦使得温度上升。图4（c）中，从齿顶的速度矢量图明显看出，压缩腔内气体存在径向和周向泄漏，方向为高压腔指向低压腔，并且由于压差，泄漏速度大于腔内气体流动速度。为了研究涡旋压缩机轴向间隙泄漏，在流场分析时，在第2工作腔轴向间隙处设置泄入测点和泄出测点，对泄漏气体速度和密度进行追踪，将测到的泄入气体密度和速度与泄出密度与速度代入方程（19），进行模拟泄漏量计算。

表1 工况参数和几何参数

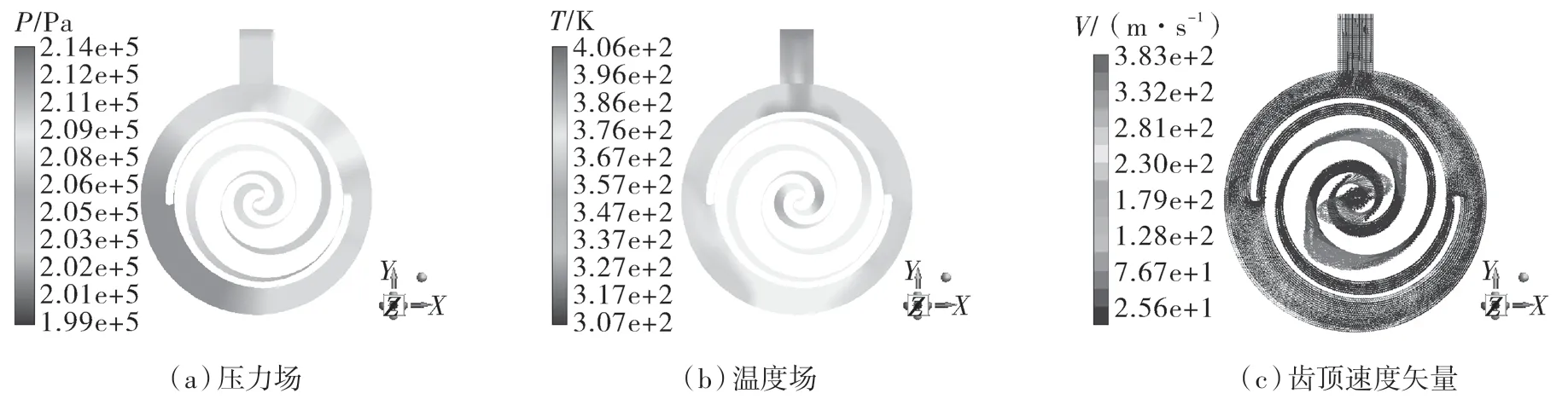
图4 流场分析结果

4 结果分析

4.1 理论计算值与模拟值比较

以某变截面涡旋压缩机为例进行计算，具体工况参数和几何参数见表1。以第2 工作腔为研究对象，分析计算第2 工作腔在一个回转周期内的泄漏变化情况，图5 示出第2 工作腔气体泄漏量的变化曲线。

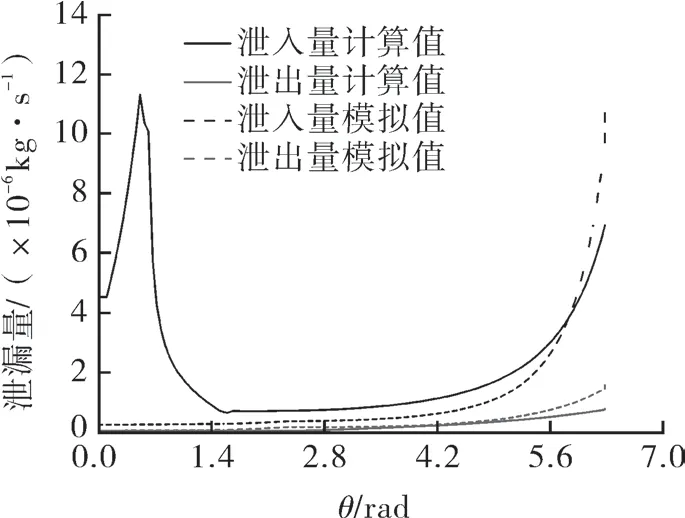
图5 第2 工作腔气体泄漏量的变化曲线

从图5 可看出，泄出率理论计算值曲线和模拟值曲线吻合较好，泄入率理论计算值曲线和模拟值曲线总体变化趋势相似，但在θ小于1.4 rad时，两者相差较大，这是因为选择以吸气完成时刻主轴转角θ为0 时刻，在数值模开始时第1 压缩腔和第2 压缩腔压差很小，气体泄漏速度很小。而在理论计算时，以整机为研究对象，本次吸气结束，第1 工作腔正在压缩上次吸入的气体，所以，第1 工作腔和第2 工作腔的压差较大，泄漏很快，待上次气体排出后，计算值和模拟值结果相近。

4.2 基圆半径对泄漏的影响

根据齿厚与展角的函数关系，代入相应计算参数，得出齿厚随展角的变化规律，图6 示出不同基圆半径的齿厚随展角的变化曲线，图7 示出不同基圆半径下第2 工作腔气体质量变化曲线。

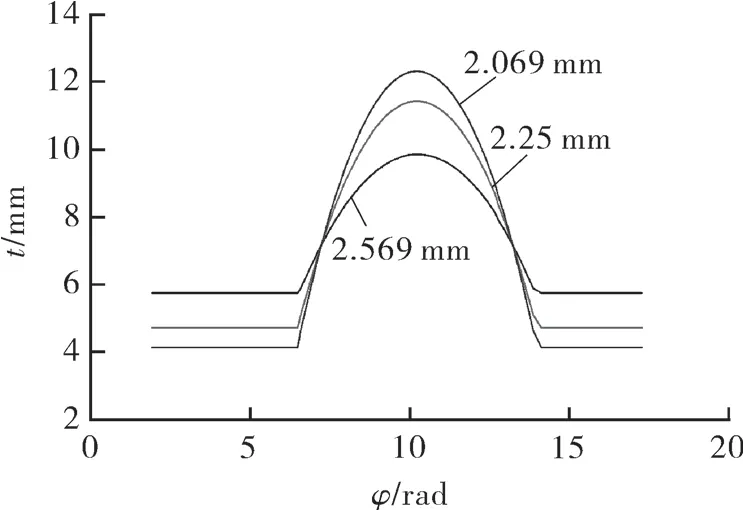
图6 不同基圆半径的齿厚随展角变化

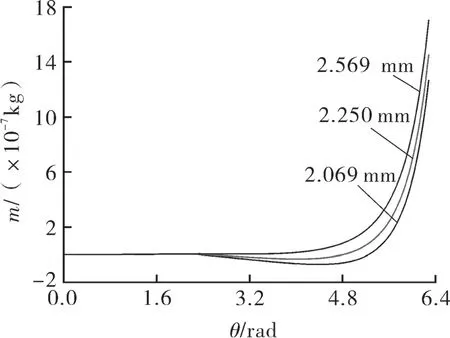
图7 基圆半径与第2 工作腔质量变化的关系

从图6 可知，展角对应型线为圆渐开线和连接圆弧时，齿厚不变，基圆半径越大，齿厚越大；展角对应型线为高次曲线时，齿厚呈抛物线分布，基圆半径越小，齿厚越大，并且变化幅度越剧烈。从曲线图7 可以看出，泄漏量与基圆半径成正比，主轴转角θ在0.75π 以前，3 种基圆半径的泄漏均非常小，说明泄入量和泄出量相当；基圆半径为a1、主轴转角θ在0.75π 和基圆半径为a2、主轴转角θ在0.8π 时，泄漏量出现负值，说明第2 工作腔的泄出量大于泄入量，当主轴转角大于1.78π 时，泄漏量均急剧上升，分析其原因，除了第1 工作腔和第2 工作腔压差大于第2 工作腔和第3 工作腔压差的原因外，此时第1 工作腔径向泄漏线由圆渐开线+修正圆弧组成，齿厚较小，第2 压缩腔基线由圆渐开线和高次曲线组成，根据轴向间隙泄漏量计算模型可知，齿厚较大，泄漏量减小。

4.3 轴向间隙大小对泄漏量的影响

为了定量分析轴向间隙大小对泄漏的影响程度，为合理控制间隙提高理论依据，计算了第二工作腔在不同间隙时气体泄漏量。图8 示出不同轴向间隙泄入量变化曲线。

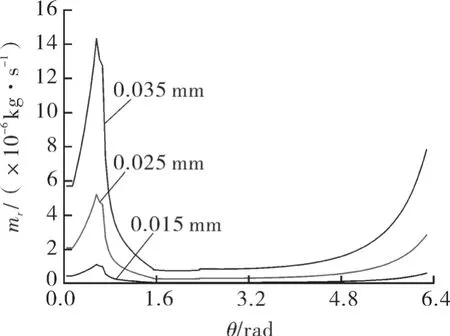
图8 不同轴向间隙径向泄入量变化曲线

从图8 可知，整体泄漏曲线类似浴盆曲线，泄漏量大是因为相邻压缩腔压差大造成的，间隙越大泄漏量越大，但二者不是简单的倍数关系，轴向间隙值大于0.025 mm时，泄漏量成近似3倍增加，因此为了控制轴向间隙泄漏，轴向间隙的大小应该控制在0.025 mm 以下较为合理，间隙过小虽减小了径向泄漏，但会造成动静涡旋盘摩擦增大。