涡旋压缩机零部件振动贡献的试验研究

刘利波，武 涛

（1.神华准格尔能源有限责任公司选煤厂，内蒙古薛家湾 010300；2.江苏开沃汽车有限公司，江苏徐州 221000）

0 引言

涡旋压缩机具有体积小、重量轻、结构紧凑以及零部件较少等优良特征［1-2］。涡旋压缩机作为一种新型容积式压缩机，近年来已被广泛应用于汽车空调、气体压缩、发动机增压以及燃料电池等诸多技术领域［3-4］。当前，涡旋压缩机具有良好的市场需求，未来前景可期。

涡旋压缩机在设计过程中，转子系统已经考虑了静平衡和动平衡问题，通过增加静平衡铁装置实现了动涡旋盘的自身静平衡；同时，分别在曲轴和皮带轮上安装两块平衡铁，实现了曲轴旋转过程的动平衡。因此，由于自身的结构优势，涡旋压缩机振动问题一直以来没有成为研究者关注的热点议题。在实际工作过程中，涡旋压缩机振动不但是影响其自身润滑与密封的关键问题，还将由于振动引发各类故障，影响涡旋压缩机的 工作。

相关研究者已经开始逐渐关注涡旋压缩机振动的研究。桂伟兵等［5］在涡旋压缩机振动原因分析的基础上，提出了一套振动测试系统方案，开展了相关试验研究工作。杨猛等［6］开展了涡旋压缩机振动测试研究，利用有限元软件对涡旋压缩机结构模态分析，明确了振动的固有频率和共振位置，制定了减震措施。刘涛等［7-8］建立了变频涡旋压缩机振动测试系统，在仿真软件平台上采集了振动信号，确定了振源所在，并提出了相应的减振措施。王珍等［9］利用结构声辐射原理和神经网络优化方法，开展了涡旋压缩机振动和噪声信号的测试，验证了方法的适用性。刘振全 等［10］建立了涡旋压缩机振动的数学模型，在频率范围内进行了振动信号功率谱分析，为样机设计与测试提供了依据。武涛［11］运用层次分析法开展了涡旋压缩机各零部件的振动贡献分析，选择了多个特殊点的位置，获得了关于涡旋压缩机振动的有益结果。Lee［12］为了减少涡旋压缩机振动引起的噪声详细的分析识别了噪声源。Kim 等基于线性循环系统分析了涡旋压缩机噪声和振动源并且对其传输路径进行识别［13-22］。

由此可知，现有研究成果由涡旋压缩机机构模型对振动进行了深入研究，提出了不同的测试方法和有限元软件工具，从振动和噪声两方面出发，通过构建振动测试平台获取涡旋压缩机的振动特征，并以此提出了减振的合理化方案。研究过程中，关注了涡旋压缩机的整体模型，针对零部件振动特征关注较少，而不同零部件的振动情况有所差异，并不了解实际工作中的零部件的振动情况。因此，探讨零部件对整机振动的贡献具有重要的现实意义，可以确定零部件的实际振动情况，明确振动特征的差异性，对分析和解决涡旋压缩机整机振动问题提供新的思路。虽然已有涡旋压缩机振动贡献量相关的研究工作，但在计算方法和判断依据方面尚有改进空间。本文将实现涡旋压缩机零部件对于压缩机整体振动贡献的量化分析，借助试验研究获得贡献比值的数据，不但可以直观地发现涡旋压缩机不同零部件的振动活跃度，还可以为压缩机分析、设计或者故障诊断研究提供有力支持。

1 技术分析

将涡旋压缩机运行系统简化为多输入单输出系统，其中零部件振动信号为多输入信号，整体振动信号作为单个输出信号。根据输入信号时域特征值的大小选择研究对象。利用研究对象间的互功率谱划分信号的频率范围，根据相干函数，判断各频率范围内研究对象的信号受到其他信号的干扰程度，利用希尔伯特变换验证范围的准确性和细化频率范围。计算输入与输出信号之间的偏相干函数，制定关于偏相干函数和互功率谱的判断矩阵标度方法，最后根据层次分析法，获得输入信号在不同频率下的振动贡献以及对于整体振动的贡献值。

1.1 信号时域分析

以均方根值和方差作为评价指标，均方根值代表了振动信号的强度，方差表示信号波动偏离程度，其定义如下：

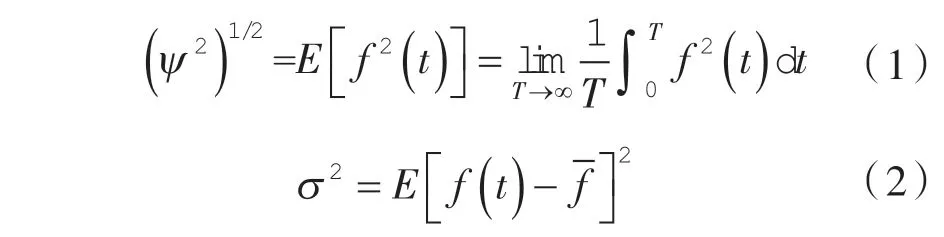
式中 ψ ——均方根值；

σ2——方差值；

E［］——期望；

T ——时间；

f ——时域信号；

对不同振动信号进行对比研究，获得不同零部件位置的振动强弱等级，以确定振动较强的位置为研究对象。

1.2 信号干扰与相关性分析

可以采用功率谱密度函数分析振动信号。互功率谱值表示了信号功率与频率之间的变化关系，可以描述涡旋压缩机每个零部件位置点振动信号中不同频率的能量，便于找出各峰值频率，进行频率分区范围的划分。相干函数描述了两个信号在各频率下的依赖程度，可以研究在特定频率范围内，振动信号采集点之间的干涉程度。

功率谱密度函数与相关函数计算方法如下：

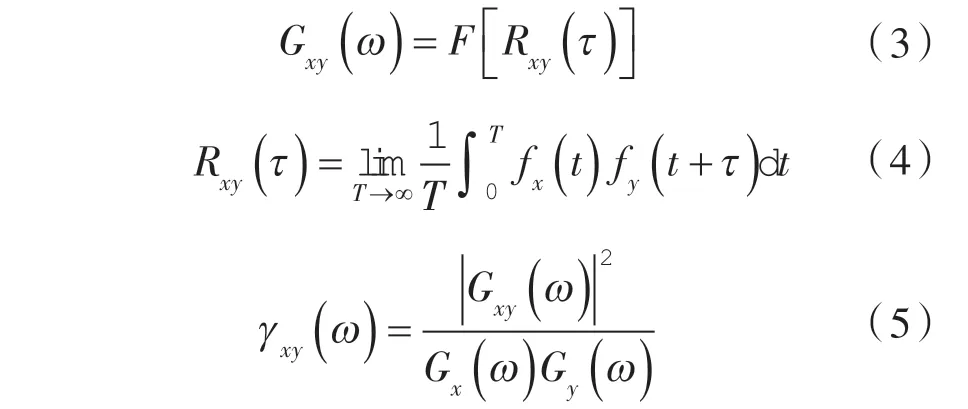
式中 Gxy——信号间的互功率谱；

F［］——傅里叶变换；

Rxy（）——信号间的互相关函数；

γxy——相干函数；

τ ——时间间隔。

根据互功率谱划分信号的频率范围，可以利用相干函数判断各频率范围内研究对象的信号受到其他信号的干扰程度。

根据柯西积分定理可知：

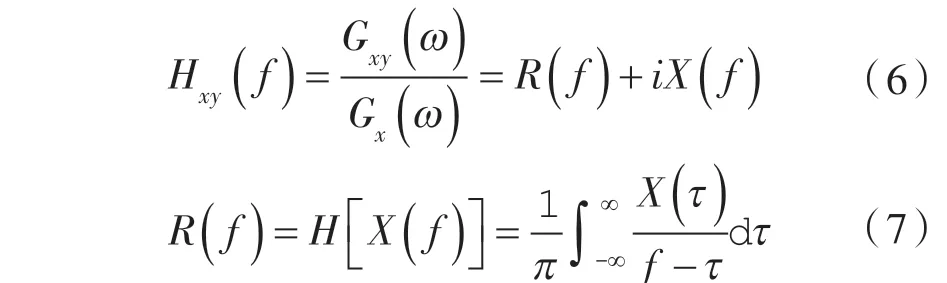
式中 Hxy（f）——信号的频率响应函数；

R（f）——实数函数；

X（f）——虚数函数；

H［］——希尔伯特变换。

对R（f）和H［X（f）］两个函数进行曲线拟合，若在某段频率范围内满足希尔伯特变换对关系，说明在此范围内两信号之间有干扰，在计算偏相干函数时需要剔除其中一个信号。利用希尔伯特变换可以进一步细化频率范围。

偏相干函数表示在剔除干扰信号后输入与输出信号的相关性，其定义如下：

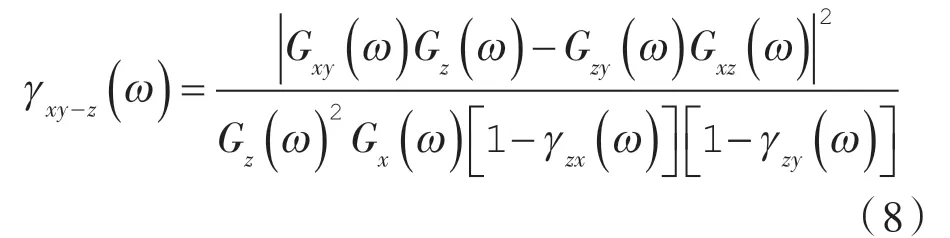
式中 γxy（ω）—— 分析信号x 与信号y 之间偏相干函数；

z ——需要剔除的干涉信号。

利用偏相干函数，可以求解零部件测试位置点与涡旋压缩机整机振动信号之间的干涉关系。

1.3 零部件振动贡献比值

根据整机振动信号的自功率谱划分其频率范围，求解不同频率范围内的振动能量所占百分比，分别用α1，α2，α3，…，αn表示。

根据输入和输出信号间的偏相干函数以及互功率谱，确定判断矩阵标度，其中标度数值一般为，数值大小表示信号之间的权重。由判断矩阵标度得出输入信号在输出信号各频率范围内的判断矩阵，再对其进行一致性验证，验证方法如下：

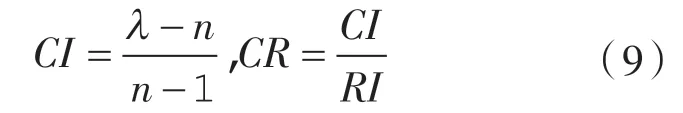
式中 CI —— 一致性指标；

n ——矩阵阶数；

λ ——判断矩阵的最大特征根值；

CR —— 一致性比率；

RI ——随机一致性指标。

当CR ＜0.1 时，认为判断矩阵的不一致程度可以接受，否则需要重新构造判断矩阵标度，然后再次进行条件检验。校验合格后，方可对判断矩阵归一化处理，得出在输出信号的不同频率范围内各输入信号贡献百分比 β1，β2，β3等。

由此，可以将不同频率范围内的振动能量百分比，与相对应的贡献百分比，获得零部件振动信号占整机振动的贡献值η：

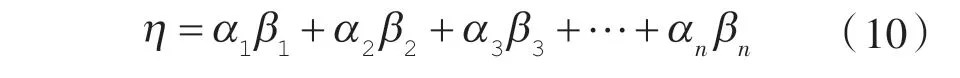
2 试验系统

试验系统包括AEW15A-0.8 型涡旋空气式压缩机一组，包括两个压缩机并联运行，测试过程针对其中一台进行。测试对象压缩机的排气量为1.0 m3/min，吸气压力为大气压，排气压力0.8 MPa；电机功率为15 kW，每台压缩机功率为 7.5 kW，工作过程中电机工频转速1 460 r/min。测试系统包括INV9822 压电加速度传感器，INV306U 数据采集仪和计算机信号采集与处理软件。试验过程中，用压电式加速度传感器进行测量，通过采集仪进行采集处理信号，最后导入PC 机读取并处理数据，获得最终的结果。

开展涡旋压缩机的振动试验测试，需要确定测试位置，如图1（a）所示。选取了1-5 为各零部件振动测试位置，排气管道位置为P1，静盘位置为P2，防自传机构位置为P3，传动轴主轴承位置为P4，皮带轮连接处为P5。而P6 为地脚螺栓连接位置，作为整机的振动测试位置。振动传感器工作频率范围0.5～8 kHz，均安装在机体表面的螺栓上，如图1（b）所示。

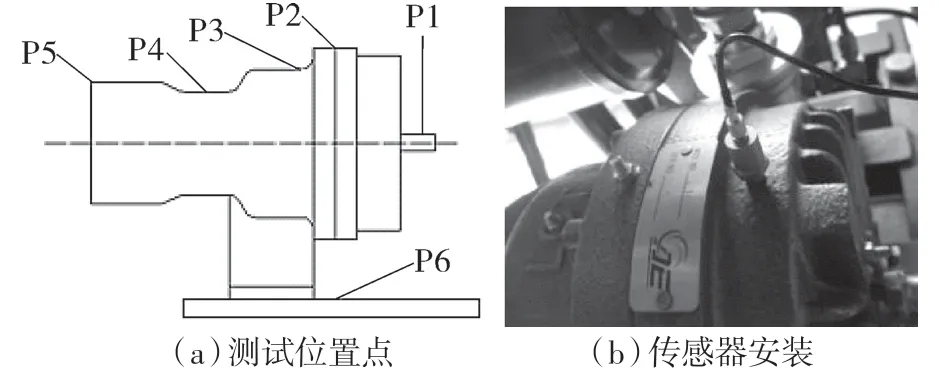
图1 涡旋压缩机振动测试位置

3 试验结果分析

3.1 信号时域分析

涡旋压缩机各零部件1 至5 位置的振动时域信号，如图2 所示。

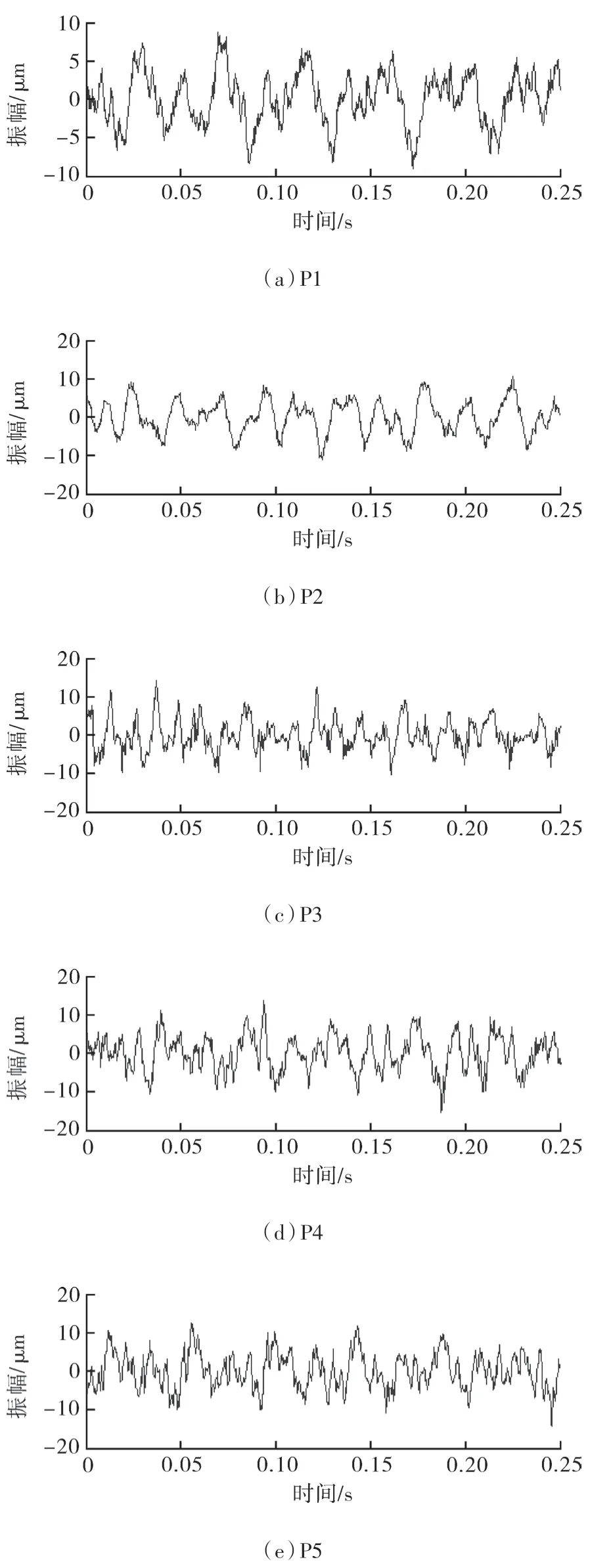
图2 涡旋压缩机振动时域信号

通过比较振动时域信号可以发现，5 个位置的均方根值最大为P1 位置5.131，最小为P3 位置3.06，分析获得均方根值排序为P2＞P5＞P4＞P1 ＞P3。信号方差最大为P2 位置21.32，最小为P1位置10.23，排序为P2＞P5＞P4＞P3＞P1。由此可以看出，P1 和P3 位置的振动较小，可以选择振动较为剧烈的P2，P4，P5 位置作为研究对象。

3.2 信号相互干扰分析

以Point 2 为例进行分析，计算获得互功率谱G24，G25如图3 所示，确定各处波峰所对应的频率数值。

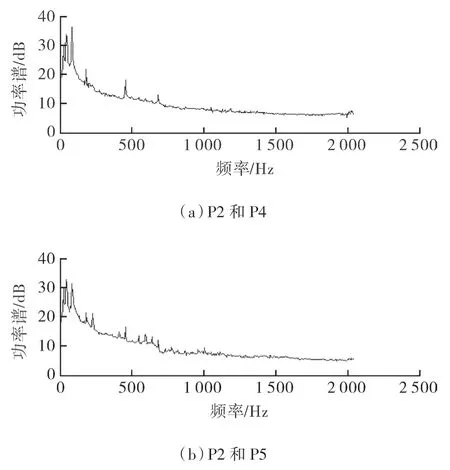
图3 互功率谱信号

P2 位置的相干函数γ24，γ25如图4 所示。

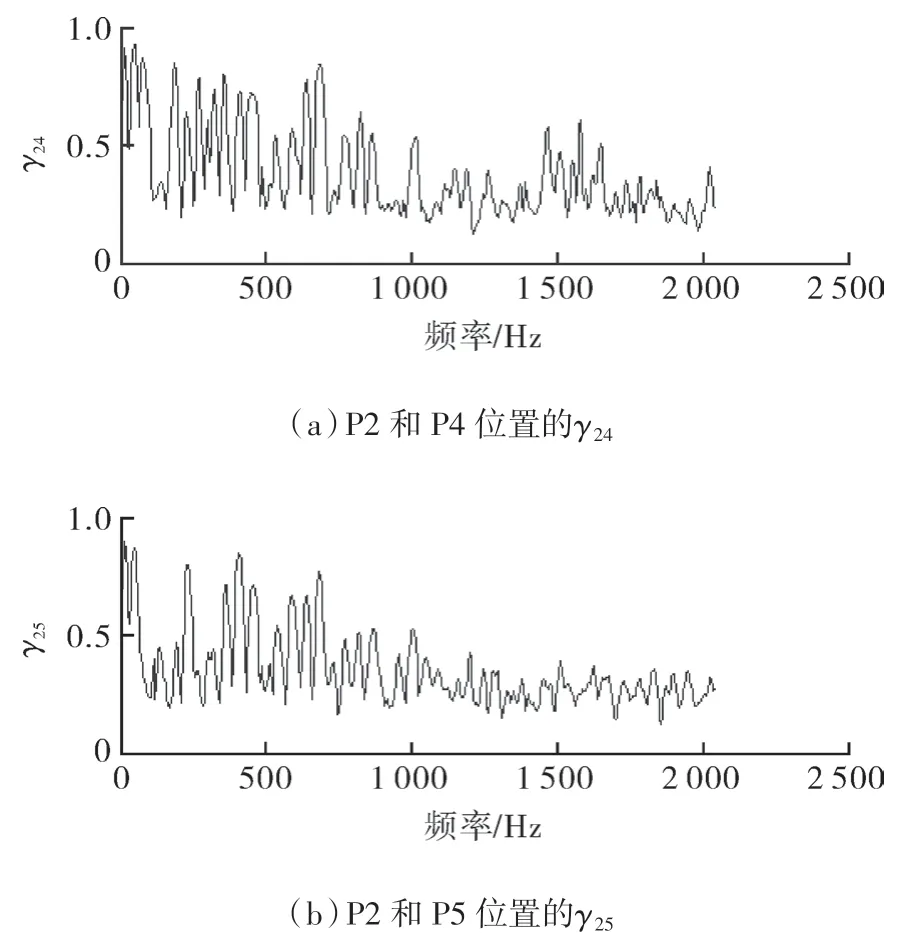
图4 相干函数

对P2 位置的振动信号进行划分，获得频率范围及其相干函数值，如表1 所示。从表可以看出，只有当频率小于100 Hz 的范围内相干函数值有明显差别，其余范围差别小，划分范围过于粗糙，难以判断P2 位置与P4，P5 位置振动依赖性。为了更细致的划分频率范围，利用希尔伯特变换图分析。

计算P2 位置与P4，P5 位置振动的频率响应函数H24，H25，对每个函数的虚部进行希尔伯特变换，再与实部进行曲线拟合，对由此细化点P2 位置的频率范围，计算范围内相干函数值，如表2 所示。

表1 P2 位置 γxy 和 γxz 平均值

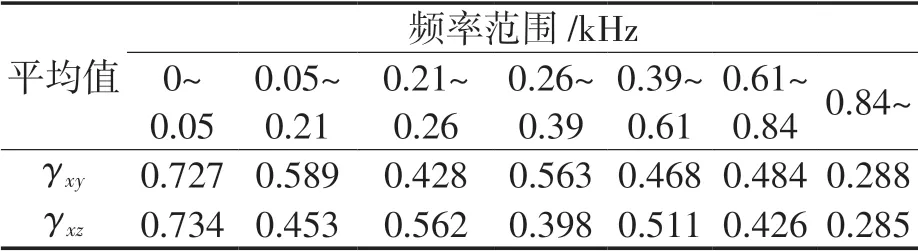
表2 细化的频率范围 及γxy 和γxz 平均值

3.3 偏相干函数计算

计算P2 位置与整机振动P6 的偏相干函数时，需要在［50，210］、［260，390］、［610，840］的频率范围内剔除P4 的信号干扰，在［210，260］、［390，610］的频率范围内剔除P5 的信号干扰。同理，可以计算出P2，P4，P5 与P6 位置的偏相干函数如图5 所示。

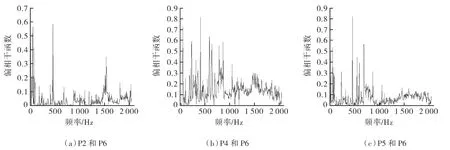
图5 偏相干函数结果

3.4 振动贡献量

对地脚螺栓P6 位置处振动进行分析，获得自功率谱G6如图6 所示，由此划分整机振动P6信号的频率范围，计算各范围所占能量比值α。

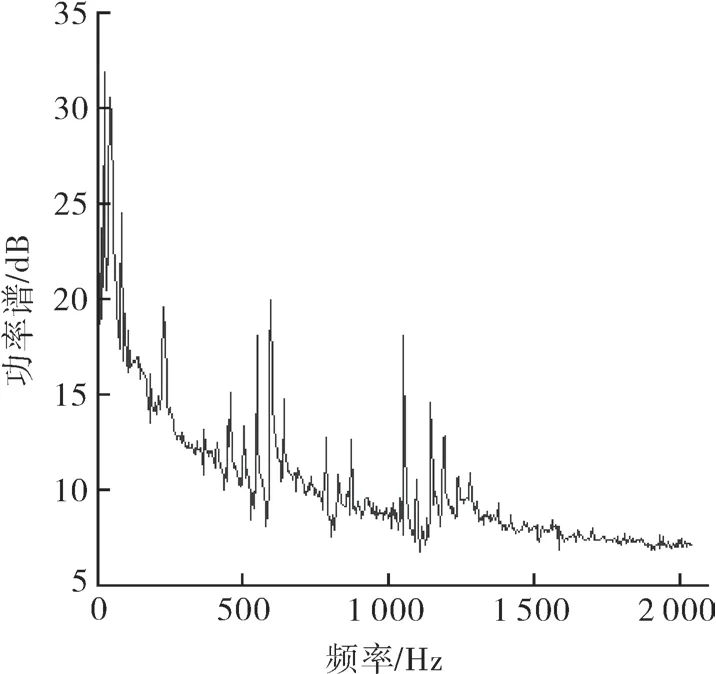
图6 P6 位置的自功率谱

分别以各零部件位置P2，P4，P6 为输入，整机振动位置P6 为输出，构建二者之间的互功率谱结果，如图7 所示。

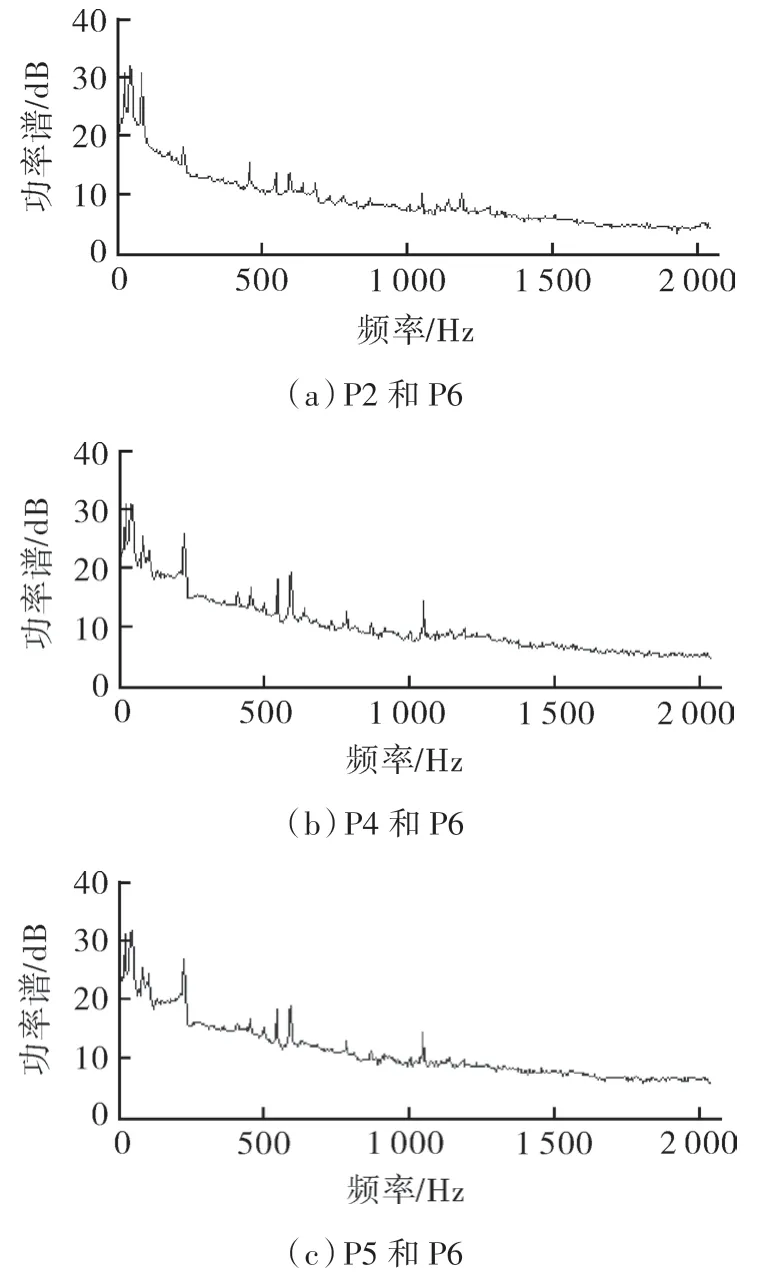
图7 互功率谱示意

建立偏相干函数和互功率谱的判断矩阵标度，如表3 所示。表中Δ 表示两个信号的偏相干函数或者互功率谱之间的差值。在获得各频率范围下的判断矩阵后，进行随机一致性指标RI 检验，实现归一化处理。

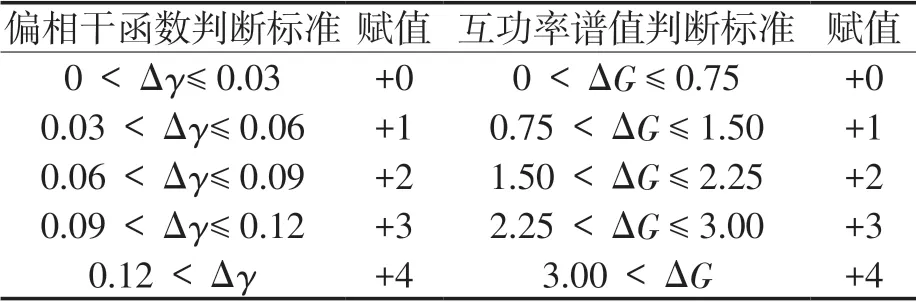
表3 判断矩阵标度

在不同频率范围内，可以计算出各零部件位置的振动贡献量及贡献比值，结果如表4 所示。

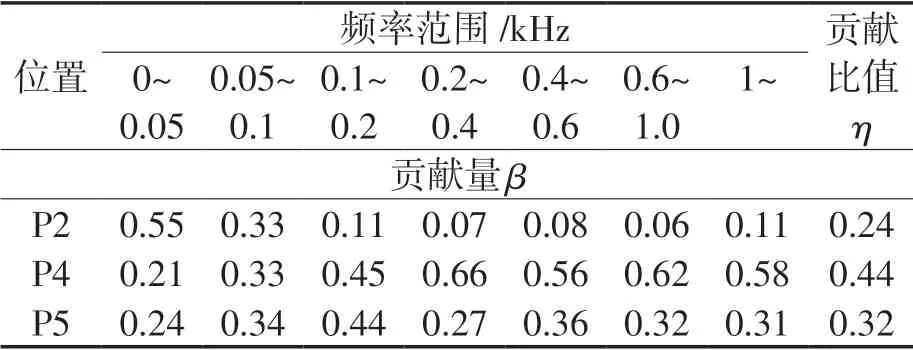
表4 各频率范围内零部件位置贡献比值

由表4 可知，对于涡旋压缩机各零部件振动，在低频范围内静盘位置P2 振动对整机P6 位置的振动贡献最大，随着频率增加贡献逐渐减小，而传动轴主轴承P4 位置的振动贡献则与之相反，其振动贡献量随着频率增加而增大。皮带轮连接处P5 位置的振动贡献，在不同信号频率范围内相对较为稳定，数值差异较小。三个主要振动的零部件位置，对压缩机整机振动贡献量中，传动轴主轴承P4 位置的振动贡献最大，其次为皮带轮连接处P5 位置，静盘P2 位置最小。

涡旋压缩机传动轴主轴承P4 位置，振动主要来源于曲轴转子系统。转子系统包括了曲轴、动盘、皮带轮和两个平衡铁。影响曲轴振动的因素较多。首先，动盘安装在曲轴端部的曲柄销上，工作中动盘作为偏心质量将引起离心惯性力失衡，虽然采用两个平衡铁进行载荷平衡，但由于加工误差、材料密度、安装精度等原因，离心惯性力引起的振动不可避免。其次，动盘在工作过程中受到的气体力和背压腔作用力不平衡，导致转子系统存在轴向位移，这将引发曲轴转子振动。

4 结论

（1）把涡旋压缩机整机振动系统简化为多输入单输出系统是可行的，运用层次分析法选取的输入与输出信号之间的偏相干函数和互功率谱作为判断矩阵标度，能够更好的分析涡旋压缩机零部件对整机振动的贡献比值。

（2）不同频率范围内振动贡献量存在差异性，低频范围内静盘P2 位置振动贡献最大，当频率高于100 Hz 时传动轴主轴承P4 位置振动贡献逐渐增强。皮带轮连接处P5 位置的振动贡献相对稳定。

（3）对于涡旋压缩机整机振动而言，传动轴主轴承P4 位置振动贡献最大，贡献比值为0.44，可以将传动轴主轴承位置作为整机振动的敏感测量点，曲轴转子系统动平衡是引发整机振动的主要来源。