组合式滤筒脉冲反吹清灰过程的数值模拟研究

祝 叶，左 丹，杨晓光，鄢恒飞，龙新平，4，季 斌

（1.武汉大学 水射流理论与技术湖北省重点实验室，武汉 430072；2.武汉大学 动力与机械学院，武汉 430072；3.九江 七所精密机电科技有限公司，江西九江 332000；4.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072）

0 引言

当前的除尘设备主要以电除尘器、袋式除尘器和滤筒除尘器为主。滤筒除尘器是在袋式除尘器的基础之上发展起来的，具有体积小、效率高、阻力损失低、维护和管理简单等优点［1］，广泛应用于食品、电力、冶金、化工、建材等工业领域，取得了良好的社会和经济效益［2-6］。

含尘气体进入滤筒除尘器后，粉尘沉积在滤料表面，滤筒除尘器的阻力随滤料表面粉尘层厚度的增加而增大，当阻力达到某一定值时就要进行清灰过程。清灰过程是滤筒除尘器中最为关键的一步，清灰效果的好坏与滤筒除尘器的效率、运行阻力及使用寿命等息息相关。目前工程上常用的清灰方式主要是脉冲喷吹清灰。针对滤芯上的灰尘堆积过程，Aroussi A 等［7］通过试验和数值模拟结合的方式进行了研究，并分析了影响灰尘堆积的因素。杨迪等［8］通过正交试验的方法得到脉冲清灰的设计参数如喷吹压力、喷吹管径等对清灰效果的影响。在脉冲喷吹过程中，清灰气流对滤筒的冲击起决定性作用，清灰时滤筒侧壁的压差峰值和压差峰值到达时间是衡量清灰效果的重要指标［9］。数值模拟脉冲清灰过程可以直观观察到清灰气流的流场变化，对滤筒内气流均匀分布设计有很好的指导作用［10-11］。

传统的滤筒一般为圆柱形，不利于反吹清灰。锥形组合式滤筒将2 个锥形滤筒组合在一起，增大了滤筒上部的清灰面积，可以有效地解决这一问题。但目前关于锥形组合式滤筒清灰过程的研究还很少见。因此，本文利用Fluent 软件对滤筒除尘器脉冲清灰过程进行数值模拟，采用不同的喷嘴形式——无散射器拉法尔喷嘴、带散射器拉法尔喷嘴，对组合式滤筒清灰性能进行研究，对比分析不同喷嘴型式的清灰机理及其清灰效果。

1 物理模型及简化

在计算过程中，将物理问题进行了简化，只考虑单个滤筒的喷吹过程。图1 示出滤筒除尘器脉冲喷吹过程。箭头代表的是正吹积灰过程，含尘气流经过滤筒过滤，粉尘则被捕集在滤筒外表面。

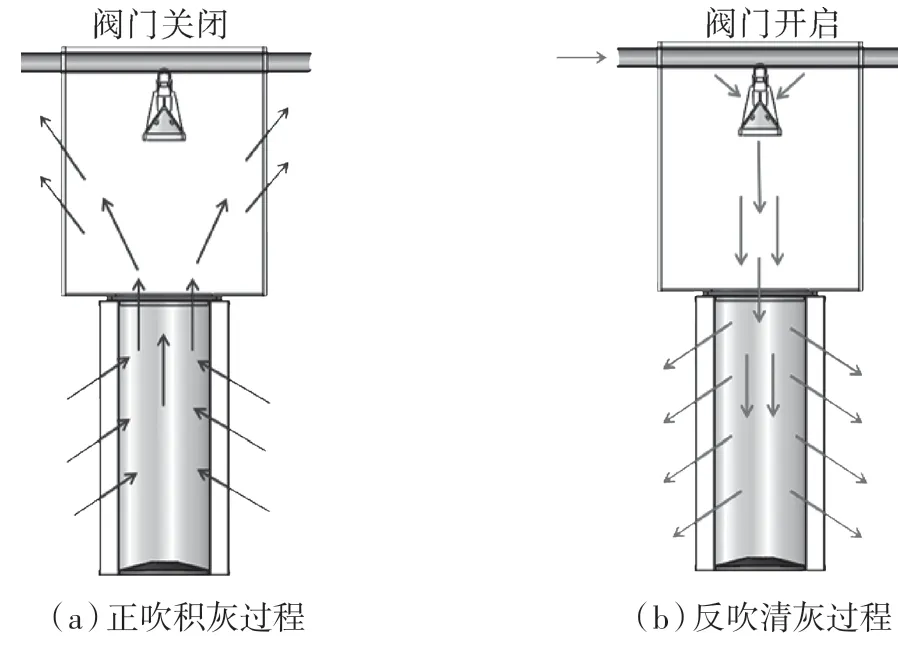
图1 脉冲喷吹过程示意（与实际模拟模型不成比例）

正吹积灰过程中滤筒上不断积聚灰尘，当进气气流阻力达到设定值时，由压差控制仪控制相应的电磁阀，打开处于闭合状态的脉冲阀，开始进行反吹清灰过程。滤筒出气口反向布置一路压缩空气，并在每个滤筒单元上方安装一个喷嘴与散射器，高压空气经过喷嘴形成高速流体，高速流体进入滤筒，与周围流体发生卷吸及能量交换，滤筒内外压差的作用将滤筒表面的灰尘振落，完成反吹清灰过程。

图2示出本文进行比较的2种形式喷嘴剖面，喷嘴进口直径为22 mm。两者主要的不同是带散射器喷嘴在拉法尔喷嘴下部加了气流散射器，散射器的结构形状使得气流均匀散射，改变了流场分布，进而影响清灰效果。图3 示出组合式滤筒尺寸。

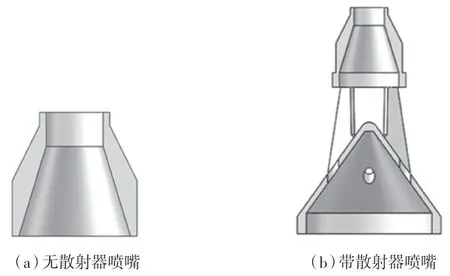
图2 喷嘴剖面示意

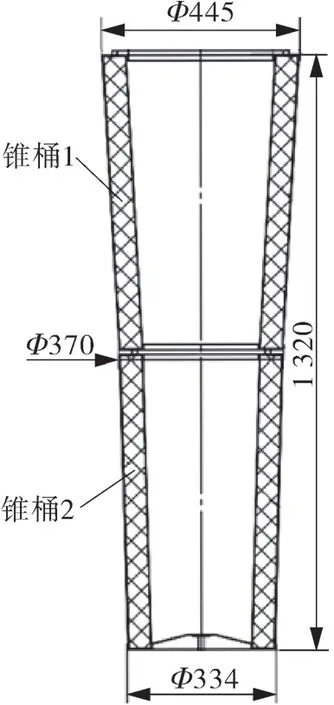
图3 组合式滤筒尺寸示意

2 数值计算方法及设置

2.1 控制方程与湍流模型

控制方程为雷诺平均N-S 方程和质量守恒方程，湍流的模拟采用S-A 湍流模型。相对于两方程湍流模型，S-A 模型的计算量较小，稳定性较好，计算网格在物面处不需要很精细，与代数模型的网格量级相当即可。同时它包含了一组新的方程，在该方程组中，不需要计算与剪切层厚度相关的长度尺度，这使得S-A 模型易用于非结构网 格中。

S-A 模型的偏微方程为：

式中 Gv——湍流黏度；

μ ——分子运动黏性；

Yv——壁面区域的湍流黏性损失；

σ，Cb2——待定常数。

2.2 多孔介质模型

在计算过程中，滤筒设置为多孔介质域，其余为流体域。多孔介质模型可以应用于多种物理问题，包括过滤纸，多孔板及流量分配器等。多孔介质的作用是通过在动量方程中增加一个源项来进行模拟，源项由两部分组成：黏性阻力项和惯性阻力项。

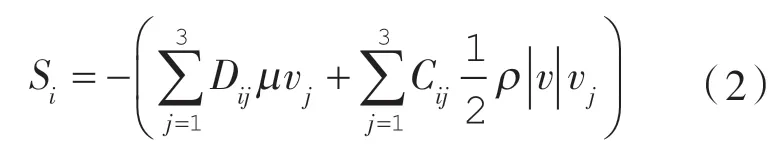
式中 Si——i 向（x，y，z）动量源项；

D，C ——规定的矩阵；

v ——速度大小。

2.3 计算域及边界条件设置

图4 示出数值模拟计算确定的计算域。在滤筒单元上方取长宽都为0.5H、高为0.2H 的长方体单元，喷嘴及扩散器都位于本单元内，H 为组合式滤筒高度。正吹积灰过程时，反吹管入口设为壁面，而反吹清灰过程时，反吹管入口设置为压力入口，大小为0.6 MPa，即脉冲喷吹压力为0.6 MPa。滤筒外表面设为压力出口，大小为700 Pa，滤筒上方的长方体外表面同样设为压力出口，大小均为一个大气压。时间步长取1×10-5s，计算收敛标准为10-5。图5 示出计算过程中监测点位置分布，上滤筒设置13 个监测点，下滤筒设置12 个，无散射器喷嘴模型与带散射器设置一致。

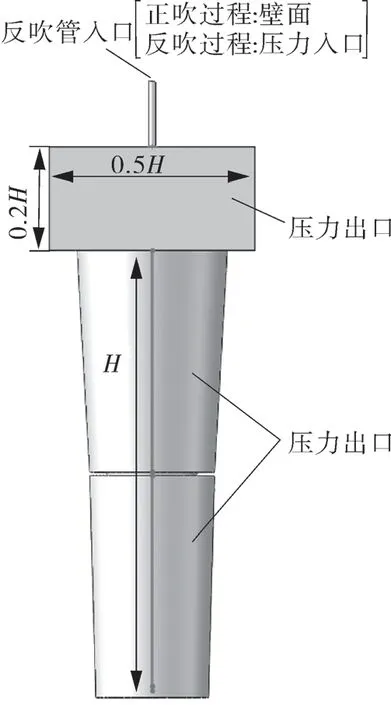
图4 计算域及边界条件

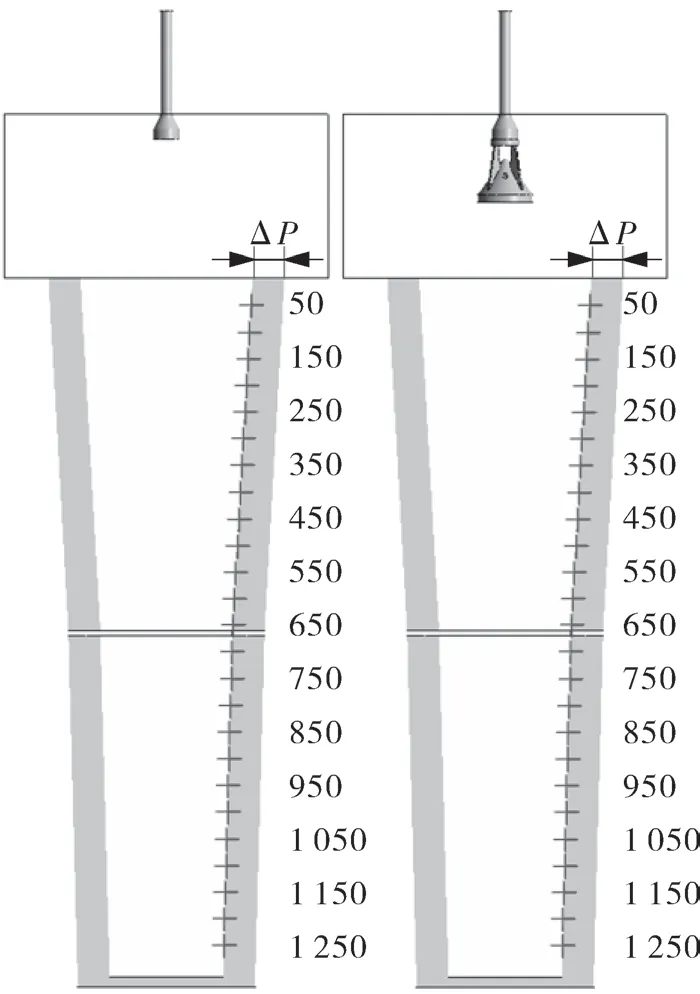
图5 监测点位置分布

2.4 网格划分

网格的划分对计算结果至关重要，本文采用笛卡尔CutCell 网格对模型进行网格划分。CutCell 网格采用自动修边的独立分片网格划分方法，能对单个零件或多个零件的流体进行网格划分，网格生成效果比四面体网格好。图6，7 分别示出2 种模型网格划分示意。经计算与网格无关性分析，确定最终的网格数为无散射器喷嘴模型网格数为265 万，带散射器喷嘴模型网格数为354 万。

图6 无散射器喷嘴模型网格划分

图7 带散射器喷嘴模型网格划分

3 模拟结果及分析

3.1 速度分析

图8 示出无散射器喷嘴模型脉冲喷吹过程速度云图。图8（a）（b）所示时刻，滤筒内进行的是正吹积灰过程，此时正吹气流形成的势流核由组合式双锥形滤筒底部逐渐上升至喷嘴位置，锥形滤筒内气流较为规律，而在靠近喷嘴位置处，由于滤筒内流道变化以及喷嘴周围壁面对气流的反作用，导致靠近喷嘴位置处，气流较为紊乱。由于正吹过程中滤筒上不断积聚灰尘，在图8（c）所示时刻，进气气流阻力达到设定值时，由压差控制仪控制相应的电磁阀，打开处于闭合状态的脉冲阀，开始进行反吹清灰过程。之后，从图8（d）～（h）所示时刻，高压空气经过喷嘴形成高速流体，高速流体进入滤筒具有明显的流核，呈现出典型的射流特性，且反吹过程中的势流核心强度明显高于正吹过程。在脉冲喷吹过程中，喷吹流体作用于滤筒壁面后，利用内外壁面的压差将正吹过程中附着于滤筒壁面上的灰尘脱落，达到清灰的 目的。

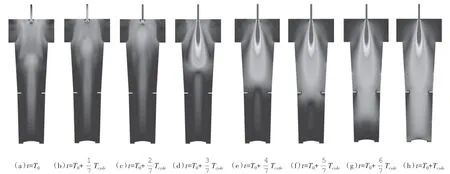
图8 无散射器喷嘴模型脉冲喷吹过程速度云图

图9示出了带散射器喷嘴模型脉冲喷吹过程速度云图。图9（a）（b）所示时刻为正吹积灰过程，但由于散射器的存在，喷嘴附近的气流呈现出与无散射器时不一致的流场，靠近壁面处出现了旋涡状气流，更为复杂。同样在所示时刻，脉冲阀开启，反吹清灰过程开始。高压气流自喷嘴喷出后，散射器的分散作用使得气流在滤筒上部开始扩散，气流动压转化为静压，导致喷吹气流比无散射器时较早地作用于锥形滤筒表面，上滤筒的清灰面积变大，且上滤筒侧壁压差峰值较大。同时，由于气流的膨胀伴有能量损失，导致带散射器时射流的势流核心区没有无散射器时明显，整体呈现出一个较为平均的速度场。继续发展，气流在进入下滤筒时气流量减小，速度也越来越小，与上滤筒的高速形成一个 反差。

图9 带散射器喷嘴模型脉冲喷吹过程速度云图

3.2 压力分析

3.2.1 监测点压力分析

取上滤筒350 mm 和下滤筒950 mm 处作为监测点，锥形组合滤筒脉冲清灰过程中的壁面压差如图10 所示。在无散射器和带散射器喷嘴模型下，进入锥形滤筒内的气流压差随时间的变化都呈现出波动状态，但两者在压差峰值以及峰值到达时间上有所不同。图10（a）示出了无散射器喷嘴模型下的压差随时间变化，在350 mm 位置处，脉冲气流进入到锥形滤筒内之后，大约6.5 ms 达到一个壁面压差峰值，其大小为258 Pa。随着脉冲气流的不断涌入及在滤筒内充分发展，经过24.6 ms 时间间隔后，气流到达下滤筒950 mm位置并产生此处的一个壁面压差峰值，其值为 164 Pa。脉冲气流压差峰值的相继达到，说明峰值气流的到达是一个与时间相关的连续性过程，而在此过程中，由于部分气流从滤筒排出，导致950 mm 位置处的压差峰值小于350 mm 处。

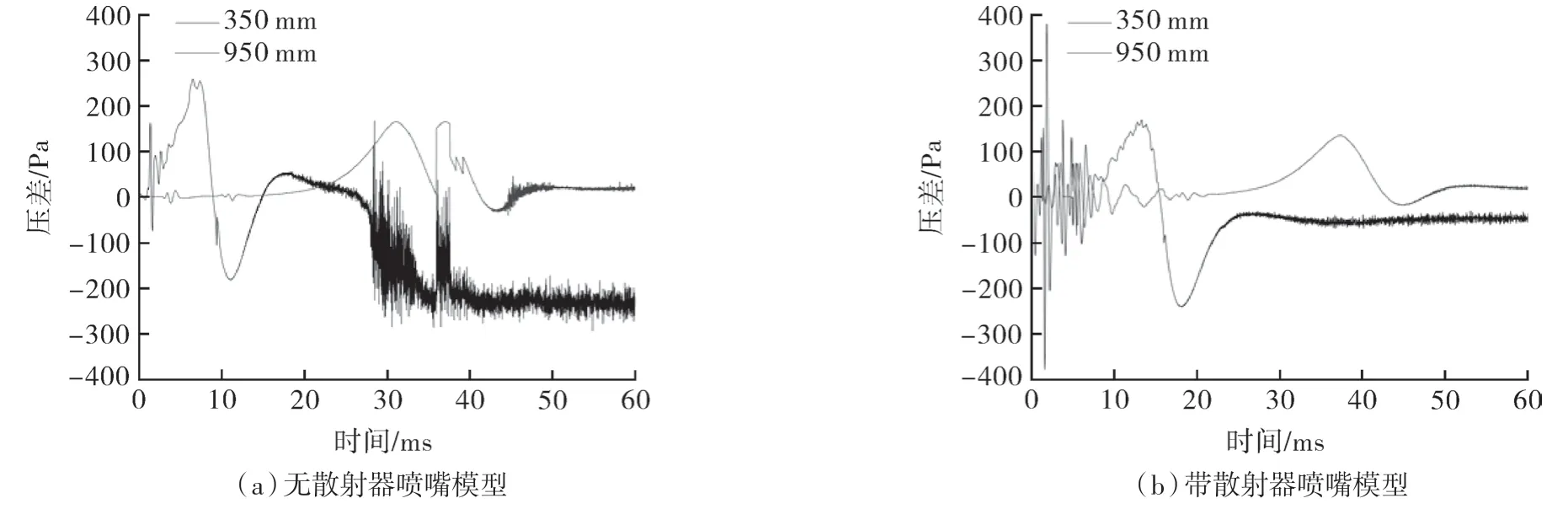
图10 监测点处无散射器和带散射器喷嘴模型的压差随时间变化

图10（b）示出了带散射器喷嘴模型的压差随时间变化情况，在上滤筒350 mm 处，脉冲气流达到此处的一个压差峰值需要1.8 ms，其值为 379 Pa。扩散器的作用使得峰值到达时间比无散射器喷嘴模型小，压差峰值大。而随着脉冲气流向下不断扩散，达到950 mm 处的压差峰值需要 33 ms 的时间间隔。脉冲气流经过相同距离，带散射器喷嘴模型要比无散射器时所需时间长，气流不再呈现出一个均匀连续态势。在下滤筒950 mm 处，压差峰值为134 Pa，其值比无散射器情况小。因此，通过对固定监测点的压差峰值及峰值到达时间的比较，认为带散射器喷嘴模型对上滤筒的清灰效果较好，下滤筒较差，上下滤筒的压差峰值的差异较大，同时带散射器喷嘴模型的喷吹气流在时间连续性上没有无散射器喷嘴模型好。

3.2.2 沿流向压力分析

图11 示出了反吹压力为0.6 MPa 条件下，无散射器喷嘴模型滤筒侧壁压差峰值及峰值到达时间分布情况。从图可以看到，滤筒侧壁的压差峰值沿滤筒长度方向呈减小的趋势，除了两滤筒组合（650 mm）处由于气流的集聚导致静压升高，但上滤筒压差峰值与下滤筒整体相差不大，导致清灰力度较均匀。同时，可以看到沿滤筒长度方向测点的压差峰值到达时间增长呈线性关系，可近似认为进入滤筒的峰值气流作用于滤筒壁面是一个连续传递的过程，这样使滤筒壁面负荷较均匀，有助于提高清灰效率，延长滤筒的使用寿命。

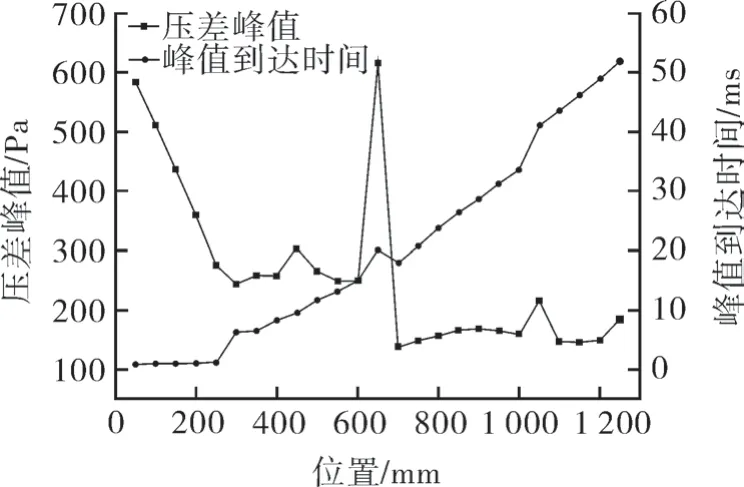
图11 无散射器喷嘴模型的流向变化

图12示出了带散射器喷嘴模型滤筒侧壁压差峰值及峰值到达时间分布情况。对于带散射器喷嘴模型，脉冲气流由于散射器的作用在滤筒上部开始扩散，气流动压转化为静压，使得上滤筒侧壁压差峰值较大。从图中可以看出，带散射器喷嘴模型滤筒上部压差峰值明显比无散射器喷嘴模型大，而下滤筒压差峰值大小相似，这就导致带散射器喷嘴模型上滤筒压差峰值与下滤筒整体相差较大，清灰压力不均。同时，可以看到上滤筒峰值压力到达时间与下滤筒差距较大，不能看作一个连续的过程。由于散射器对气流的散射作用，气流在进入下滤筒时气流量减小，速度也会越来越小，下滤筒的压差峰值是由于气流到达滤筒底部后形成的反吹气流的作用。这再次说明上滤筒与下滤筒壁面负荷不均匀，不利于提高清灰效率。

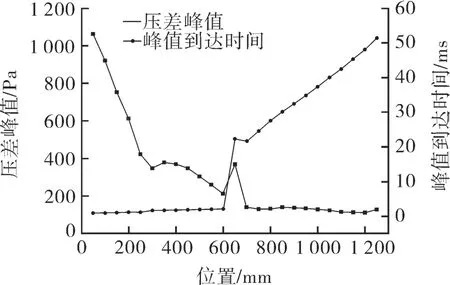
图12 带散射器喷嘴模型的流向变化

因此，对于无散射器喷嘴模型，脉冲清灰气流沿滤筒长度方向从上而下作用，清灰力度较均匀，受力时间连续，清灰效果较好。而对于带散射器喷嘴模型，上滤筒与下滤筒清灰受力时间不连续，导致清灰力度不均匀，清灰效果较差。

4 结论

（1）利用S-A 湍流模型及多孔介质模型，对2 种不同喷嘴型式的组合式滤筒进行了脉冲反吹清灰过程的数值模拟。将清灰时滤筒侧壁的压差峰值和压差峰值到达时间作为清灰效果的重要指标，从固定监测点和沿流向2 个方向分析了2 种模型的清灰效果。

（2）无散射器拉法尔喷嘴模型对组合式滤筒清灰效果良好，而带散射器拉法尔喷嘴模型对上滤筒清灰效果较好，下滤筒清灰效果较差。