基于改进的K-Means 算法在SNP 选择中的应用∗

陆信蓓 周从华 张付全 张 婷 蒋跃明

（1.江苏大学计算机科学与通信工程学院 镇江 212013）（2.无锡市精神卫生中心 无锡 214151）（3.无锡市妇幼保健院 无锡 214002）（4.无锡市第五人民医院 无锡 214073）

1 引言

单核苷酸多态（Single nucleotide polymorphism，SNP）主要是指在基因组水平上由单个核苷酸的变异所引起的DNA 序列多态性。SNP 数据作为重要的基因变异数据，是目前生物信息学领域中的重要课题之一，其具有数量多、分布广等特点，适合于对复杂性状与疾病的遗传解剖以及基于群体的基因识别等方面的研究。但SNP 数量多而存在的SNP 数据维度高的特点使得SNP 数据中存在较多的冗余和噪声，这就使得从大量的SNP中选择具有代表性的SNP 子集即选择特征SNP 子集势在必行。

由于SNP 数据普遍存在少样本、高维度的问题，和SNP之间存在连锁不平衡性使得SNP位点之间存在强相关性的特点，本文考虑了SNP之间的相关性，将互信息引入K-Means 算法，提出了一种新的聚类算法——K-MIM。并将其与蚁群算法结合应用于SNP选择中，提出一种新的SNP选择方法。

2 相关工作

2.1 SNP选择的研究

目前SNP 子集的选择主要方法包括基于统计的关联研究方法和基于机器学习的特征子集选择方法。全基因组关联研究（Genome-Wide Association Study，GWAS）通过对比患病组和健康组的SNP 位点，可以发现与疾病相关的致病基因，其关键在于提高统计检验效能，降低假阳性。基于机器学习的特征子集选择方法主要包括过滤式和包裹式两种选择策略。其中过滤式选择其优点在于计算量小可以处理大规模数据，但忽略了遗传变异之间的相互作用；包裹式选择是将评价指标和学习器结合起来，但其缺点在于计算量大选择效率较低。目前，研究学者们基于这两种方法提出了很多改进。文献［1］提出了一种基于Relief-SVM 的SNP数据特征选择方法，提高了SNP 选择的分类准确率。文献［2］针对传统的包裹式SNP选择方法计算量大，时间复杂度高的问题，提出了基于最大相关性最小冗余度（MCMR）的信息SNP 选择方法。文献［3］提出了一种基于稀疏表示的变量选择方法，改进了传统系数回归模型的变量选择能力，并将其用于SNP 选择。文献［4］采用克隆选择算法选择SNP 子集，能够更快地识别标签SNP。文献［5］提出了一种基于主变量（PV）方法的无监督SNP 选择方法，通过选择称为PV 的原始变量子集来实现维数减少，消除冗余的SNP。文献［6］提出了基于遗传的特征选择算法，使特征数量大大减少。文献［7］提出了基于条件互信息最大化和支持向量机特征递归消除融合的混合特征选择方法，取得了较高的预测准确度。

2.2 K-Means算法的研究

K-Means 算法是一种基于样本间相似性度量的间接聚类算法，可以将数据集划分成不同的簇。其具有简单、快速的特点，是解决聚类问题的一种经典算法，可应用于较多的领域。但K-Means算法也有聚类个数难以确定、初始簇中心对聚类效果影响较大等缺陷［8］，因此，研究学者们基于原始的K-Means算法提出了较多的改进。文献［9］针对分割图像经常被噪声和强度不均匀等影响的问题，提出了一种基于熵的K-Means（LCK）新型分割算法。文献［10］针对不良初始化引起的较差的局部最佳值问题，提出了MinMax K-Means算法，该算法依据方差为簇分配权重。文献［11］将遗传算法与K-Means 算法相结合，自动确定簇的数量，并生成高质量的初始簇中心。文献［12］针对K-Means 倾向于收敛于局部最优及依赖初始簇中心的问题，将K-Means 与改进的CI 结合起来，提出了一种有效的混和进化数据聚类算法。文献［13］研究了基于K-Means聚类算法的犹豫模糊聚类技术，将层次聚类的结果作为初始聚类。文献［14］针对海量数据的K均值问题的有效近似，将整个数据集划分为少量子集，每个子集的特征在于其质心和权重，再在局部表示上应用加权版本的K-Means算法，大大减少计算的距离数量。文献［15］提出一种新的判别嵌入式K-Means，将多个判别子空间的同步学习嵌入到多视图K-Means 聚类中，构建统一框架，自适应的控制子空间之间的相互协调。

3 基于改进的K-Means 算法的SNP选择方法

3.1 K-Means算法原理

原始的K-Means算法，其目标是把数据划分为k 个簇，使得同一个簇中的样本相似度越高，不同簇之间的样本相似度越低。其算法思想如下，设输入的数据集S={x1,x2,…,xn}中有n 个数据样本，确定聚类簇数k ，从数据集S 中选择k 个样本作为初始均值向量即初始簇中心{c1,c2,…,cn}，计算剩余每个样本与各均值向量的距离，将样本划入与之最近的一个簇中心点所在的簇，更新均值向量，重复以上过程，直到目标函数收敛，或簇中心不再改变或改变很小，聚类算法停止。

其中，K-Means算法常用的距离度量为欧式距离，其定义如下：

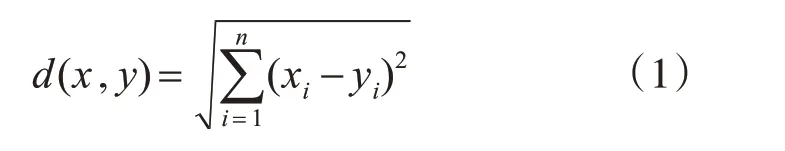
式中，n 代表样本的属性数目，xi和yi分别为样本x 和样本y 的第i 个属性。

K-Means算法常用的目标函数为平方误差，其定义如下：

3.2 改进的K-Means算法——K-MIM

虽然K-Means算法的原理较为简单，且收敛速度快，实现容易，算法的可解释性强，但是其仅在簇的平均值可被定义的情况下才能使用。而由于SNPs 之间存在连锁不平衡性而导致的位点之间具有强相关性的特性，使得传统的K-Means算法的距离度量方式并不能挖掘出SNPs 之间的内在联系，忽略了SNP本身的特性。为此，本文提出了一种改进的融合互信息的K-Means 算法——K-MIM 算法。

3.2.1 互信息

互信息（Mutual Information）是信息论中衡量两个随机变量之间相关性的信息度量，两个特征之间的互信息越高，则这两个特征之间的相关性越强。假定两个特征x 和特征y，则两个特征之间的互信息可表示为

考虑到SNP位点之间存在强相关性的特性，本文在欧式距离中引入互信息的概念，则第一轮迭代计算中，每个特征与初始簇中心的距离度量公式表示如下：

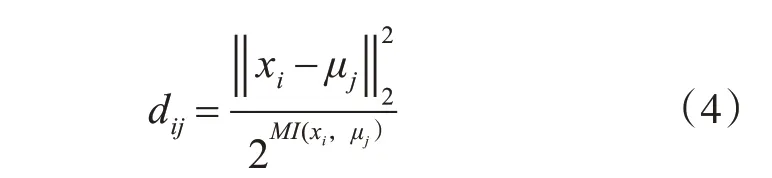
其中，‖ ‖xi-μj2表示特征xi与初始簇中心μj的欧式距离；MI(xi,μj)表示特征xi与初始簇中心 μj之间的互信息。

3.2.2 簇中心的更新

传统的K-Means 在簇中心的更新时取簇中样本的均值作为下一轮迭代中每个簇的簇中心。但在进行SNP聚类分组时，无法计算每个SNP与均值向量的互信息，进而无法进行后续迭代，因此，势必要对簇中心的更新进行改进。

本文在对欧式距离的实验中发现，在一个样本点的集合中，每个样本点与其他各点的距离之和和该点到均值点的距离呈近似的增函数。以样本点集合dataset1 为例，dataset1 中共包含100 个随机样本点，如图1 所示。以单个样本点到其他各点的距离和dsum为纵坐标，该点到均值点dxi-μ为横坐标建立二维平面坐标系，如图2 所示，dsum和dxi-μ呈现出近似的增函数关系。

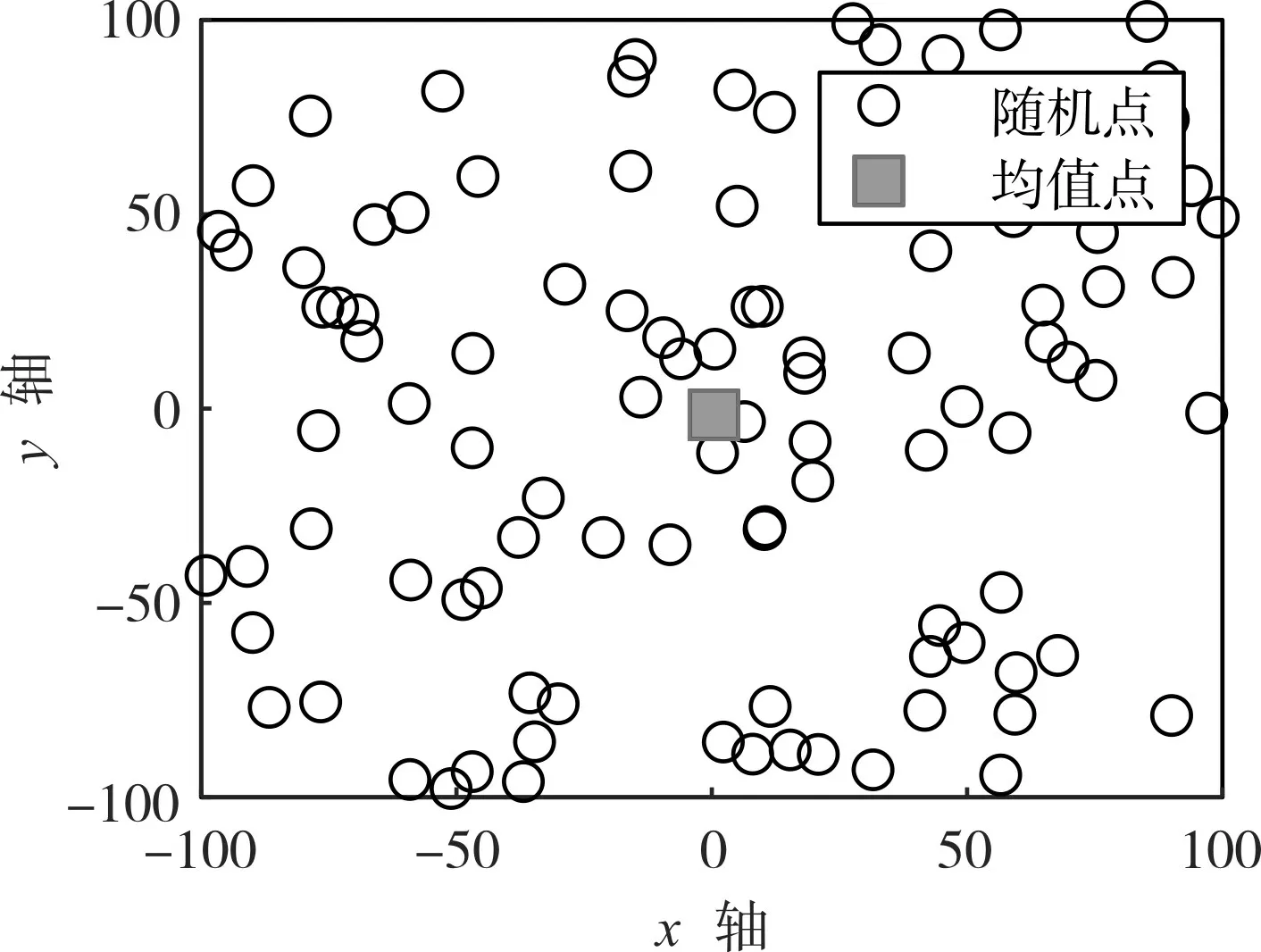
图1 数据集dataset1

图2 dsum 与dxi-μ 关系图

由此，本文将上述实验发现扩展到K-MIM 算法中，对簇中心的更新进行改进。本文提出将原有的每个簇更新后的均值簇中心用一个簇中心体代替。具体改进如下，根据式（4）在每个簇中取n 个与其他SNP 距离和最小的SNP 作为下一轮迭代的簇中心体。假设簇中心体的集合C={c1,c2,…,cn}，表示第j 个簇中心体中的第t 个SNP，则在第二轮迭代开始时，每个SNP 与簇中心体cj的距离度量公式表示如下：

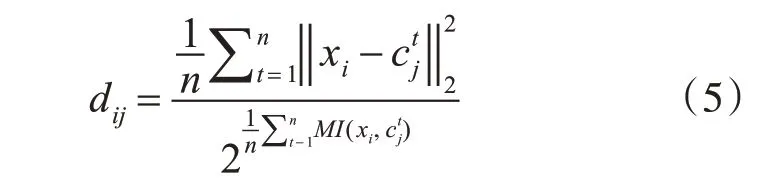
3.2.3 算法K-MIM整体步骤

结合章节3.2.1 和3.2.2，则算法K-MIM 的整体步骤如算法2所示。

算法2：K-MIM算法

1）从数据集S={x1,x2,…,xm}中随机选择k 个特征作为初始均值向量(μ1,μ2,…,μk)

2）for i=1 to m do

3）for j=i to m do

4） 根据式（1）和式（3）计算(d(xi,yi))2与MI(xi,yi)并存于表中

5）end for

6）end for

7）for i=1 to m do

8）根据式（4）计算xi与各均值向量的距离

9）将xi划入与之距离最小的均值向量所对应的簇

10）end for

11）repeat

12）根据式（4）在每个簇中取n 个与其他SNP 距离和最小的SNP作为簇中心体

13）for i=1 to m do

14）根据式（5）计算xi与各簇中心体的距离

15）将xi划入与之距离最小的簇中心体所对应的簇

16）end for

17）until 算法达到最大迭代次数，或簇中心体不再改变或改变很小

3.3 K-MIM算法在SNP选择中的应用

蚁群算法是由意大利学者Marco Dorigo提出的一种概率型算法［16］，用于寻找优化路径。结合K-MIM 算法和蚁群算法，本文首先利用改进的K-MIM 算法将SNPs 进行聚类分组，再对每个组中的SNPs 用蚁群算法筛选SNP 子集，将得到的k 个子集合并，得到的子集即为最后的信息SNP子集。

4 实验

4.1 实验环境及数据

实验环境：编译工具Python3.6.0，操作系统Windows10，CPU/Intel（R）Core（TM）i5-3230M 双核处理器，主频2.6GHz，内存8G，硬盘容量1T。

实验数据：本次实验所使用的数据由无锡市精神卫生中心提供。数据格式为基因型SNP数据，每个样本带有类标记，标注样本患病与否。具体描述如表1所示。

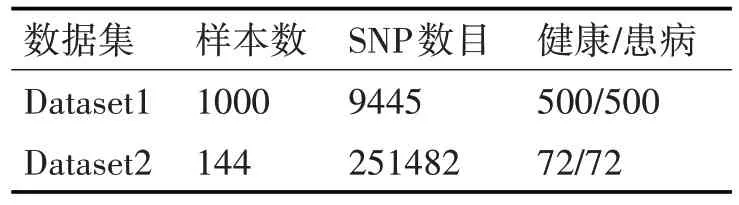
表1 数据集描述

4.2 实验评价指标

1）SNP选择的评价指标

本文使用信息SNP 子集对非信息SNP 子集的重构准确度（ACC(I)）作为信息SNP子集的评价指标，其定义为对所有非信息SNP位点预测准确度的平均值。重构度越高，信息SNP 子集对非信息SNP的预测效果越好。

2）分类效果的评价指标

本文使用F1-measure 和预测准确率（Acc）来对分类效果进行评价。

4.3 实验结果及分析

1）信息SNP选择实验及分析

在两个数据集上，分别用K-Means、K-MIM 和特征加权K-Means 算法［17］对给定的聚类数目k 将SNP 分为k 组，并采用蚁群算法对每组进行信息SNPs 进行提取，最后采用最近均值分类算法对非信息SNP 子集中的位点进行预测。实验结果如图3和图4所示。

由图3 和图5 可看出，K-MIM/蚁群算法所提取出的信息SNPs对非信息SNP 子集具有更高的重构度，且当聚类簇数为7 时，在两个数据集上均取得较好的实验结果，在后续的分类实验中，将使用簇数为7时所筛选出的信息SNP子集进行实验。

图3 Dataset1上每种算法选出的信息SNP对非信息SNP的重构度

图4 Dataset2上每种算法选出的信息SNP对非信息SNP的重构度

2）分类实验及分析

为进一步验证所选择的信息SNP 子集所包含的信息量，在该部分实验中，本文采用K-Means/蚁群算法、K-MIM/蚁群算法、特征加权K-Means/蚁群算法、ReliefF 和MCMR 算法进行信息SNP 子集的筛选，并选择了SVM、DT 和Xgboost作为分类模型，进行分类实验。实验结果如表2所示。

由表2 可看出，K-Means/蚁群算法和特征加权K-Means/蚁群算法相比，K-MIM/蚁群算法筛选出的信息SNP 子集具有更好的分类效果。此外，与ReliefF 和MCMR 两种信息SNP 选择算法相比，K-MIM/蚁群算法所选择出的信息SNP 子集在多数情况下取得了更好的分类效果。实验结果说明，K-MIM 算法在考虑SNP 位点之间的关联性进行聚类后，在SNP选择中具有较大的优势。

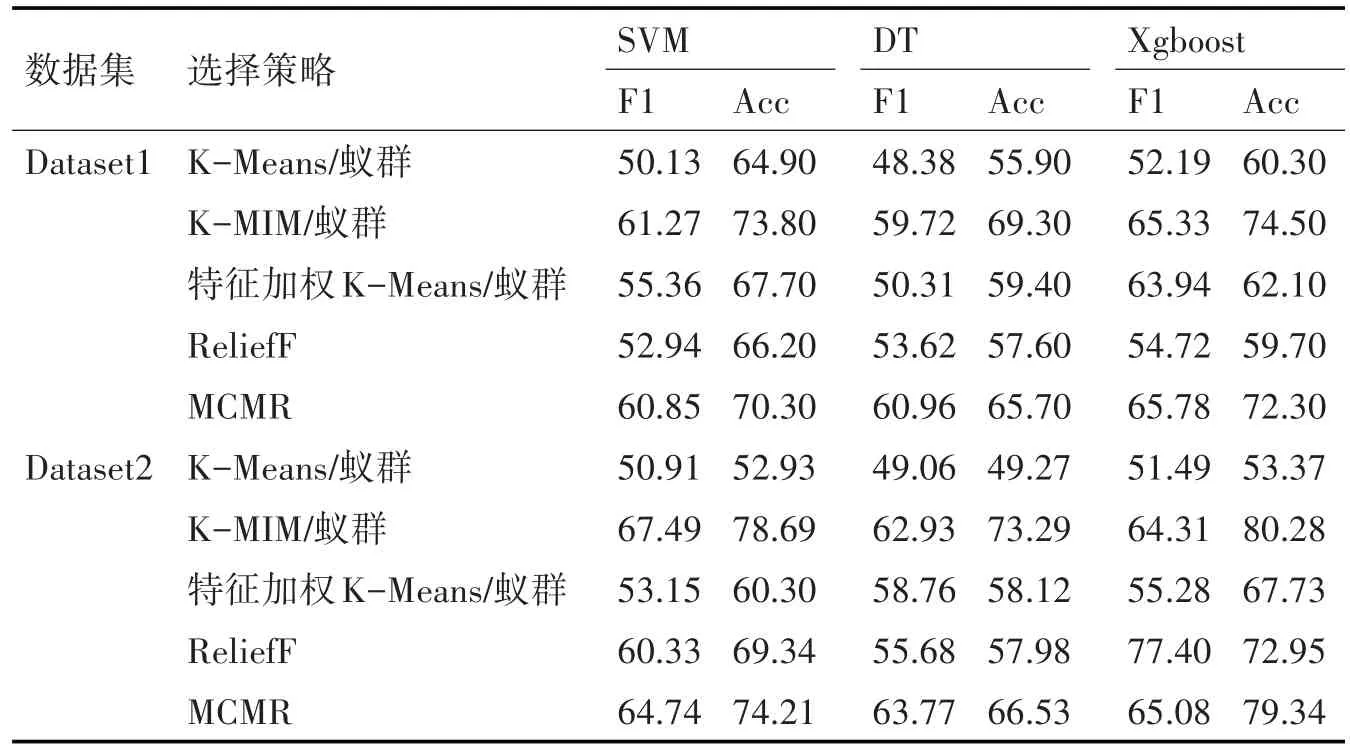
表2 信息SNP子集在不同分类器下的评价结果

5 结语

本文针对SNP数据普遍存在的少样本、高维度的问题，和不同SNP位点之间存在连锁不平衡导致的位点之间具有强相关性的特点，提出了一种融合互信息的K-Means聚类算法用于SNP的选择中，将其与蚁群算法结合使用进行信息SNP 子集的筛选。在信息SNP 选择实验和分类实验的结果中表明，K-MIM/蚁群算法所筛选出的信息SNP 子集对于非信息SNP 子集的重构和分类都具有较大的优势。本文后续工作在于对蚁群算法进行改进，使筛选出的信息SNP 子集具有更高的重构度和分类准确度。