基于遗传算法的K-means 聚类改进研究∗

冯永亮 李 浩

（1.西安文理学院信息工程学院 西安 710065）（2.西安文理学院西安市物联网应用工程实验室 西安 710065）

1 引言

作为一种经典的基于划分的聚类算法，K-means 以其运算简单快捷、资源消耗较少、伸缩性强等优势，受到业界的广泛推崇。然而该算法也存在一些不足：聚类数目无法直接得到，需要根据先验知识或者随机设置，这使得结果变得不稳定；初始聚类中心往往是随机选取的，而选取的结果又直接影响了聚类的结果。本文利用遗传算法的全局寻优特性和自适应搜索概率技术等优势来弥补K-means的劣势，形成一种改进的聚类方法。

2 K-means聚类算法

2.1 K-means概况

K-means 聚类旨在将集合分成若干个簇，尽量使簇内对象高相似，而簇间对象低相似［1］。K-means 首先在包含N 个点的集合中，随机假设K个点为起始的聚类中心，然后依据所有点到中心点的距离大小，将每个点分配到离中心点较近的簇中，再重新求出每个簇的中心点，不断重复，直至中心点不再发生变化，或者聚类准则函数收敛为止［2］。

K-means算法的基本步骤如下：

1）随机选取若干点作为起始聚类中心点；

2）将每个点划分到距离它最近的中心点所在的簇中；

3）形成每个簇中新的中心点；

4）若簇的中心点已稳定不变，或者聚类准则函数已收敛，则结束并输出结果，否则转至步骤2）继续进行。

2.2 K-means的优缺点

K-means 聚类算法的优点在于运算简单快捷，资源消耗较少，且处理大型数据库或者大数据集时，算法具备可伸缩性和高效性。同时，K-means能够有效解决分布比较均匀的数据集的聚类问题，往往应用于文本、网页和图像的聚类分析，但是，K-means 也存在一些明显的不足，主要包括：1）聚类生成的簇数K 值需要凭经验预先给定，而根据经验设定的K 值往往不是最佳聚类数目，会影响到聚类的结果［3］。2）算法容易受到初始聚类中心选取的影响，如果改变初始聚类中心，聚类结果也会随之变化［4］。3）算法是一种针对局部的搜索技术，往往寻找的并非全局最优值［5］。

K-means 聚类算法需要从三方面进行改进：1）寻找一种更优的方式来获取K 值，而不是随机或凭经验设置K 值，提高聚类效果。2）寻求更高效的方式来选取初始聚类中心，而非随机或凭经验设置初始聚类中心，提高聚类效果的稳定性。3）寻找全局性更优的算法来弥补K-means 易于陷入局部最优的不足。

3 遗传算法

3.1 遗传算法概况

为了模仿生物在自然环境中的遗传方式，人们提出了一种自适应的、面向全局的寻优搜索算法，即遗传算法［6］。该算法首先将每个可能解编码成染色体，然后随机选择若干个染色体，形成起始的种群，再根据预设的适应度函数算出所有染色体的适应值。接着选取具有较高适应值的染色体担任新的父代染色体，随后使用交叉、变异等操作产生子代染色体，即新的适应值更高的染色体，经过若干代不断繁衍，最后得到适应值最优的染色体［7］，即问题的最优解。

遗传算法运行的详细过程是［8］：

1）设置个体数，交叉概率，变异概率，终止条件等参数；

2）随机性设置双亲群体中的码串，作为初始值；

3）设置进化代数为0；

4）算出各条基因串的适应度值；

5）进行遗传操作，通过概率参数生成后代；

6）用子代更新父代，生成下一代个体；

7）如果终止条件尚未满足，跳转到步骤4）；如果已满足，则得出最优解。

3.2 遗传算法的优劣势

遗传算法的优势比较明显，主要包括：1）应用比较广泛。遗传算法并非直接处理问题的参数，而是通过编码生成的基因，任何问题通过编码成基因个体后，就可以使用遗传算法［9］。2）全局寻优特性和并行性。遗传算法在点群中而不是在一个单点上寻优，并且对搜索的多个点进行评价，这些特性既增强了算法的全局搜索能力和并行化能力［10］。3）遗传算法是一种自适应概率搜索技术，它使用概率规则，其选择、交叉、变异等操作都是基于概率进行的，使得搜索过程更加灵活［11］。虽然遗传算法具备上述优势，但也存在易过早收敛、缺乏定量分析等劣势［12］。本文考虑利用遗传算法的全局寻优特性和自适应搜索概率技术等优势，改进K-means聚类质量。

4 基于遗传算法的K-means聚类研究

4.1 基于遗传算法的K-means聚类研究现状

Krishna 将以前的遗传交叉算子更新成K-means，得出一种新的遗传算法，并证明了新算法能求出全局最优值［13］。Manlik 利用浮点数操作提升了算法的查找效率［14］。Cristofor.D 设计了一种变长基因编码，提升了聚类的效率［15］。Sarafis 将遗传算法用于构建K-means目标函数，并得出一种更高效的聚类算法［16］。武兆慧等将模拟退火算法与遗传算法有机结合，形成了一种新的聚类算法［17］。赵峰等在复合型遗传算法的基础上进行优化设计，弥补了易陷入局部最优的不足［18］。贾兆红等利用一种混合遗传聚类算法中的禁忌搜索提升了聚类速度［19］。耿跃等改进了遗传算法中的变异算子，设计出了一种新的聚类算法［20］。

4.2 基于遗传算法的K-means聚类设计

本文结合K-means的不足，以及遗传算法优劣势，考虑对K-means 进行三点改进：1）改进K-means 初始K 值的获取方式，对N 个对象的样本集N'，利用遗传算法来学习K 值，作为K-means 算法的初始K 值。2）改进K-means 初始聚类中心形成方式，利用遗传算法的自适应搜索概率技术和全局寻优特性，形成更加稳定的K-means初始聚类中心。3）进一步改进遗传算法中的选择、交叉、和变异算子，既可防止早熟现象，又能提高K-means 全局搜索能力和计算效率。改进后的算法包括以下几方面的设计。

1）生成样本集

考虑原始数据集规模大小不一，如果能够对较大规模的原始数据进行随机均匀采样，生成样本集，这样就可以更快地获取最优的K值和初始聚类中心，在此基础上，再在原始数据集上进行K-means 聚类，这样就可以提高聚类的质量和效率。具体操作是：首先判断原始数据集的个体数量，如果高于设定的阈值（一般设定为60～130），则对原始数据集进行随机均匀采样，生成原始数据集的子集，即样本集；如果低于阈值，则直接将原始数据集作为样本集。

2）遗传算法相关设计

（3）设计选择算子。遵循“优胜劣汰，适者生存”的原则，本文采用轮盘赌法，使个体被选中的概率取决于其对应的适应度值的大小，适应度值越高，其参与后代繁殖的概率越高。设为个体Xi的适应度值，P( )

Xi为个体Xi的选择概率，N 为个体数量，则：

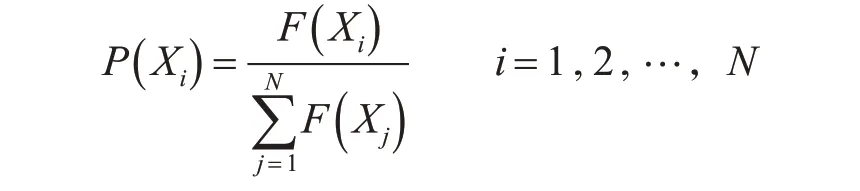
（4）设计自适应交叉算子。本文设计一种交叉概率随染色体适应度值自动变化的交叉算子，如果个体适应度值低于平均适应值，则直接进行交叉操作，相反，如果个体适应度值高与平均适应值，选择一定的交叉概率。这样既保留了高适应度值得个体特征，又保证了低适应度值个体交叉操作，进一步提高算子全局搜索能力。设Fmax为最大适应度值，Favg为平均适应度值，F'为进行交叉操作中的个体中的较大适应度值，自适应交叉概率Pc的公式为

（5）设计自适应变异算子。同自适应交叉算子类似，本文也设计了一种基于自适应概率的变异算子，如果某个体适应值高于群体平均值，则对其采用低变异率，保证使其顺利进入下一代，否则，对该个体直接进行变异操作，使其高概率的被淘汰。设F 为要变异个体的的适应度值，自适应交叉概率Pm的公式为

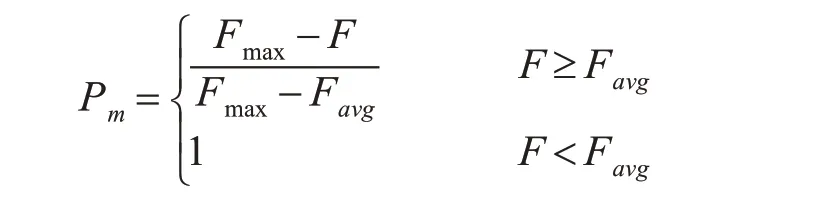
3）基于遗传算法的K-means聚类算法步骤

（1）判断原始数据集规模大小，如果小于等于设定的阈值（一般在60～130 之间），则直接将原始数据集作为样本集。否则，对原始数据集进行均匀采样，生成样本集。

（2）利用遗传对样本集K 值寻优，获得最优K值。

（3）利用上一步获得最优K 值，再次利用遗传算法对样本集寻优，获得最优初始聚类中心。

（4）利用第（2）、（3）步获取的K 值和聚类中心，对原始的数据集进行聚类操作。

（5）得到最优聚类结果。

基于遗传算法的K-means 聚类流程图如图1所示，其中利用遗传算法进行K 值寻优如图2 所示，利用遗传算法进行初始聚类中心寻优的流程与K 值寻优类似，不同的是其初始K 值是上一步寻优得到的最优K值。

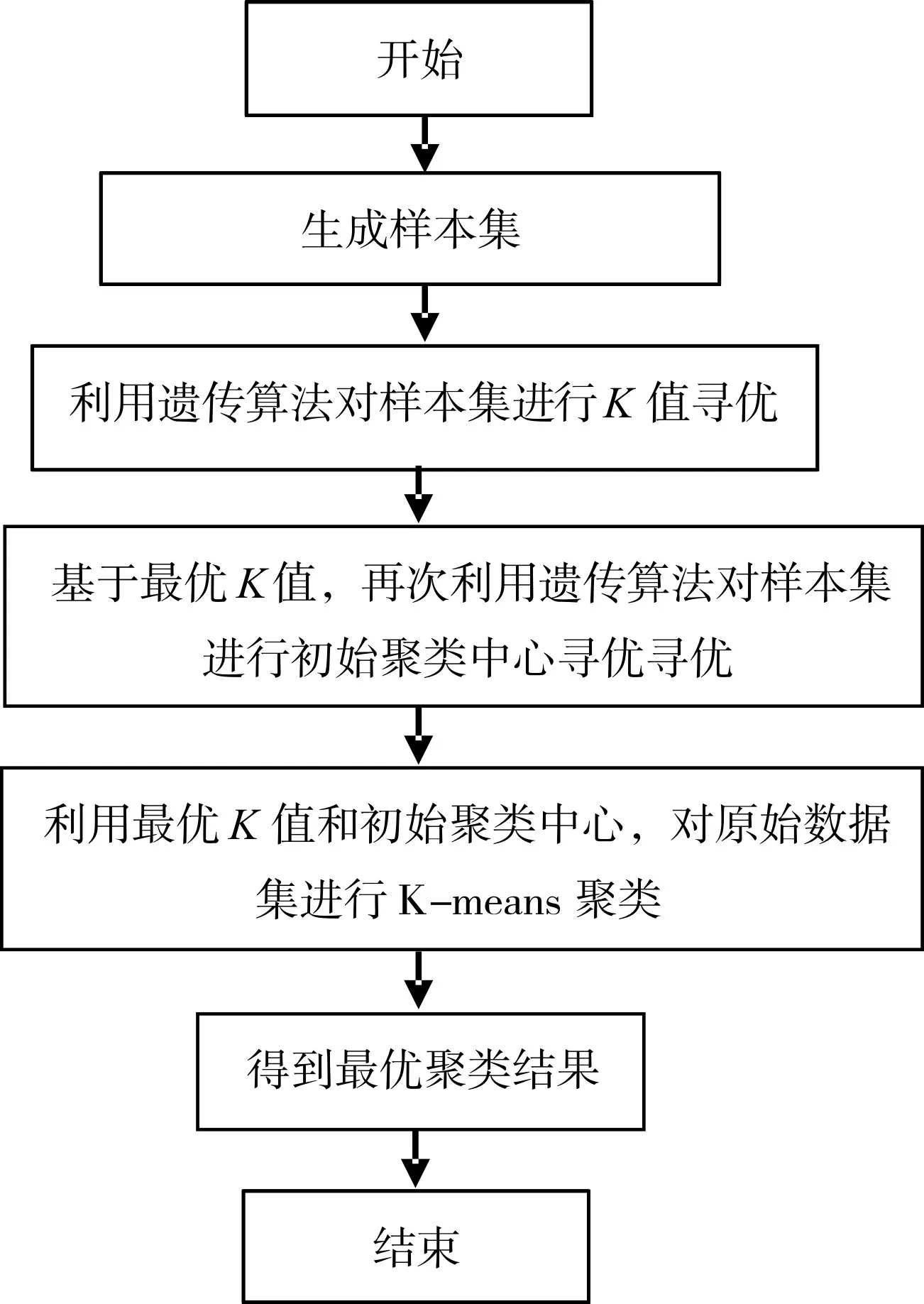
图1 基于遗传算法的K-means聚类流程图

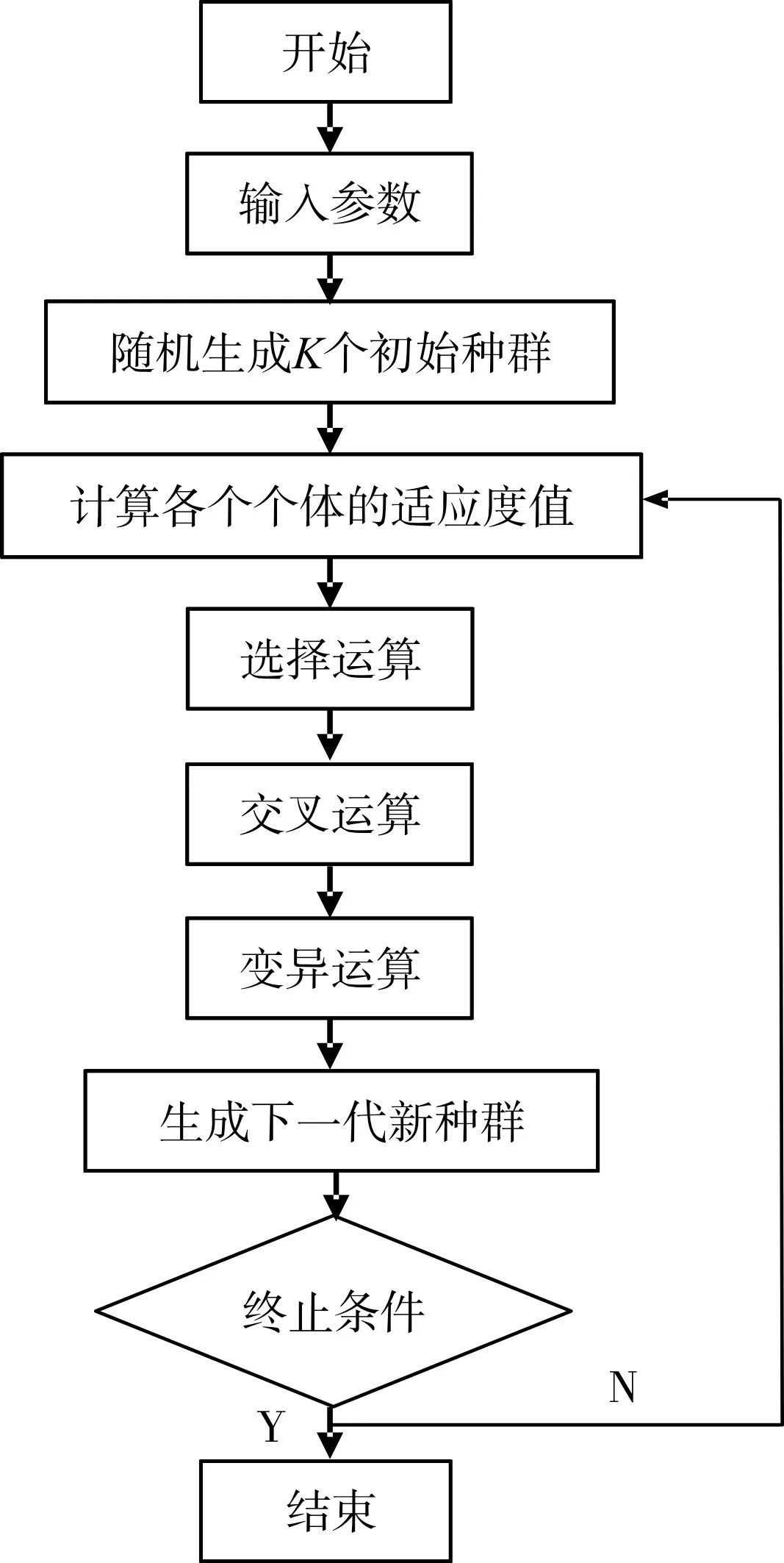
图2 利用遗传算法进行K值寻优的流程图

5 仿真实验结果及分析

实验平台包括：Intel（R）Core（TM）i5-4590 CPU 3.30GHz，4G 内存，500G 硬盘，操作系统Windows7。分别采用K-means 算法和本文算法在Matlab 环境下，对Iris 数据集（数据规模：110）和Automatives数据集（数据规模：630）进行聚类，聚类结果如表1 和表2 所示。实验表明，基于遗传算法的K-means 聚类在平均迭代次数和准确率方面明显优于普通的K-means算法。

表1 Iris数据集聚类结果

表2 Automatives数据集聚类结果

6 结语

本文针对K-means存在的若干不足，利用遗传算法的全局寻优和自适应搜索概率技术等优势，设计了一种基于遗传算法的K-means聚类算法，仿真实验结果表面，新算法在迭代次数和准确率方面均优于普通的K-means算法。