一种实现微博兴趣挖掘的粒子群优化k-means 算法∗

沈 超 王 逊 黄树成

（江苏科技大学计算机学院 镇江 212003）

1 引言

微博是人们日常交流、获取社会资讯不可或缺的一种网络渠道。由于微博用户数量的急剧增长，产生的信息量也随之呈指数级增长。一个正常的微博用户，通常每天收到的博文数高达几千甚至上万条。面对如此巨大的数据量，用户很难在其中发现感兴趣的博文，因此个性化地推荐用户感兴趣的博文就显得格外重要。在此过程中，如何快速地捕获用户在当前时间段感兴趣的话题是关键。

从文献调查中发现，微博兴趣挖掘近年来被国内外众多学者关注和研究。对兴趣挖掘的研究分为两个方向，第一个方向是对挖掘文本的选择研究，如Abel［1］等研究了微博文本长短对兴趣挖掘的影响。第二个方向是对挖掘算法的研究，如刘红兵等使用改进的Single-Pass 结合层次聚类算法对博文进行挖掘。使用聚类算法［2］对用户博文数据进行挖掘，可以很好地将相似的兴趣点挖掘出来。

目前k-means算法［3］在数据挖掘领域使用得较为广泛，使用该算法可以很准确地挖掘出用户当前时间所关注的兴趣话题。但在对微博用户大量数据处理时，时间代价较大，同时存在受初始聚类中心影响较大的缺点。因此，刘靖明提出在k-means的基础上，结合粒子群算法加以优化。综上所述，本文提出一种参数间相互作用的MPSO-kmeans 算法。该算法可以有效地节约处理时间，同时避免k-means的缺点，具有更好的聚类效果。

2 相关算法介绍

2.1 k-means算法

k-means 是聚类算法中使用场景最广泛的一种，对数据的处理过程分为两个阶段，第一阶段设置类族数量，将数据集中的每个数据分别划分到类族中某一类中，第二阶段通过迭代计算，找出聚类中心，重新划分，达到结束条件为止。该算法原理是通过计算不同空间数据的欧式距离，进行相似度分析，将相似度高的数据聚类到同一个类族。

该算法聚类步骤如下：首先输入样本S=X1,X2,X3,…,Xm。

1）设定类族数量，即算法k值；

2）随机指定k个聚类中心 μ1,μ2,…,μk,k ＜m；

4）若算法达到结束条件，则算法结束。如果没有，使用同一类簇中的数据，计算新的类簇中心，然后转到步骤2）进行迭代。

虽然k-means 具有操作简单、所需资源少、计算速度快等优点。但仍存在一些缺点：

1）该算法需先给定聚类个数，聚类个数很难估计，在知道给定数据集前，并不能确定将其分为多少类最合适；

2）算法需先设置初始聚类中心，随机选取，对导致聚类结果变化巨大；

3）迭代过程中，需要不断的计算，找出新的中心，时间开销很大；

4）若类族中存在孤立点，将导致均值偏移。

2.2 粒子群算法

粒子群算法［4］是一种基于动物集群活动而产生的群体搜索算法，该算法利用个体间信息的共享，使群体的求解从无序到有序，进而求出最优解。群体中的每个个体称为粒子。粒子在空间以随机初始速度飞行，根据个体最优位置、群体最优位置和粒子当前速度，不停地调整飞行位置和速度。

假设粒子在q 维空间飞行，那么粒子i 的位置、速度均为q 维向量，其速度可表示为优位置表示为Pbi=( Pbi1,Pbi2,…,Pbiq)，群体最优位置表示为Gb=(Gb1,Gb2,…,Gbq)。

如果找到个体最优解，群体最优解，可以使用以下公式调整粒子飞行的位置和速度：

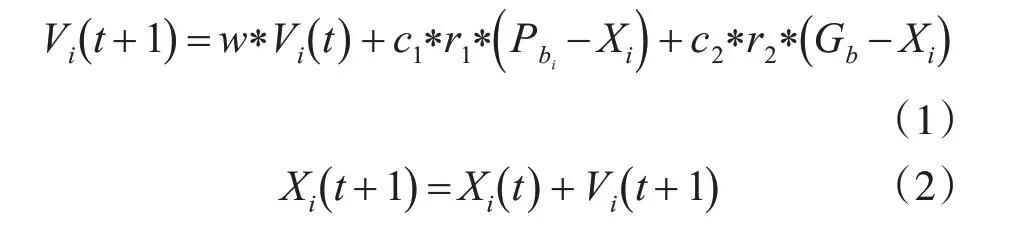
在式（1）和（2）中，w表示惯性权重，而c1，c2表示学习因子，其表示个体最优位置、群体最优位置对粒子i 飞行速度的影响程度；r1，r2为[0,1]间随机值，表示速度定义不同部分的随机权重。

粒子群算法通过计算适应度函数，对算法结果评价。设适应度函数为f(X)，则个体最优位置Pbi对应的函数为f(Pbi)，全局最优位置对应的函数为f(Gbi)。如果粒子适应度值优于个体最优值，那么用粒子当前位置替代个体最优位置。群体中适应度值最优的粒子位置，即为群体最优位置。

粒子个体最优位置更新公式，如式（3）所示：

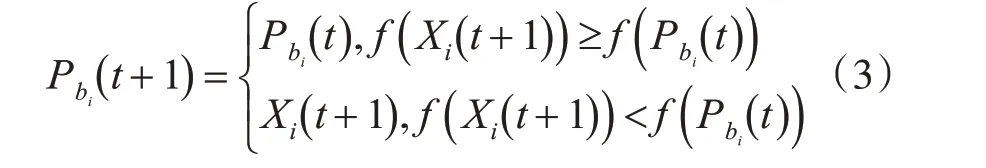
3 MPSO-kmeans算法

3.1 粒子群优化的k-means算法

k-means 是聚类算法中最经典、简单的一种，被运用到很多领域，如数据挖掘、模式识别等，但如2.1 节所介绍，传统k-means 算法仍具有一些缺点，而粒子群算法在全局搜索方面具有显著的优势，为克服k-means 中存在的问题提供了新的方案。根据上述分析，使用粒子群算法和k-means融合［5］，不仅可以提高收敛速度、减少时间代价，而且可以提高聚类效果，克服算法缺陷。

虽然这种融合算法在选取最优聚类中心方面很好地克服了k-means 的缺陷，但是并不能摆脱粒子群自身存在的缺陷，如粒子在飞行过程中，根据式（1）、（2）不断调整自身的位置和速度，而惯性权重和学习因子通常被设为固定常量，或者被设定为独立变量，这种情况下各参数之间相互削弱，难以达到全局搜索、局部开发的相对平衡；粒子在迭代飞行过程中，可能存在过于早熟现象；针对上述问题，本文对融合PSO-kmeans算法进行优化处理。

3.2 算法优化策略

1）惯性权重优化

惯性权重［6］是粒子群优化中非常重要的参数之一，通过设置不同权重，可以控制算法具有不同的全局搜索能力。较大的惯性权重有助于提升全局搜索能力，防止算法早熟。而较小的惯性权重有助于提升局部搜索精度。因此，惯性权重在一定程度上有着平衡全局和局部搜索能力［7］的作用。

在利用粒子群优化算法寻找最优解的早期，希望算法具有较好的全局搜索能力，而后期则希望其具有较高的精度搜索。因此本文引入了一种线性递减的惯性权重，该权重w 值随运行次数的增加，不断减小。最终，算法由初期的全局搜索转为后期局部的高精度搜索，权重设置如式（4）所示：

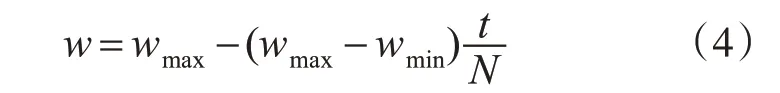
式（4）中：wmax为惯性权重最大值；wmin为惯性权重最小值；一般wmax取0.9，wmin取0.4；t 为当前迭代次数；N为最大迭代次数。

2）学习因子优化

学习因子［8］也是影响粒子飞行的重要参数之一。学习因子c1表示自我认知对飞行轨迹的影响程度，学习因子c2表示群体认知对粒子飞行轨迹的影响程度。如果c1较大，会使粒子不断地在局部飞行、震荡；如果c2较大，会使粒子过早收敛，导致早熟。为了权衡自我认知、群体认知对飞行轨迹的影响，引入随惯性权重变化的学习因子，公式如下所示：

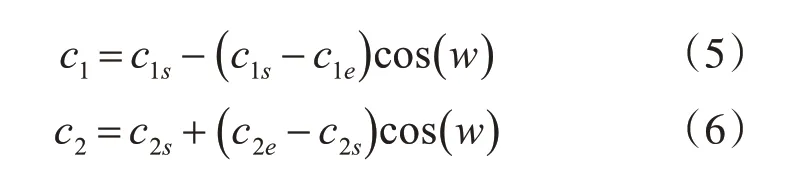
式（5）、（6）中，c1s，c2s表示对应学习因子的初始值；c1e，c2e表示对应学习因子的终止值。

3）时间飞行因子的引入

由粒子位置更新公式可知，其位置更新方式是在原位置的基础上加上粒子更新后的速度。在物理学概念中，位移只能与位移进行计算，由此可知，粒子位置更新公式中存在着隐藏的时间因子［9］。传统的位置更新公式是将时间因子固定为1，在公式上会呈现位移加速度的更新方式。但这种更新方式将会导致粒子不断在最优解附近震荡，因此在算法中引入随惯性权重线性变化的时间因子T 。令T=0.1+w，当T ≠1时，运行初期，因为惯性权重较大，时间因子也较大，粒子飞行位置保持着较大的变化，有利于全局搜索。后期由于惯性权重变小，时间因子也随之变小，粒子飞行位置保持着较小的变化，提高了局部的搜索精度。

大数据分析平台利用其分布式存储能力，通过对绿通治理相关业务数据进行采集、清洗，存储海量数据；同时，利用其并发计算能力，对海量历史数据进行分析计算，对离散的数据进行实时的在线分析计算，并将计算结果同步至系统的各子平台中。大数据分析平台采用分布式主从节点架构、集群横向可扩展和多数据副本冗余存储，确保平台稳定工作、数据安全不丢失；节点与节点之间使用RPC通信，经任务调度器实现任务资源的统一分配和统一管理。结合运维平台，更加人性化、简洁化地对整个大数据分析平台进行监控、管理，可针对分析任务的实际情况进行调优，提升大数据平台的分析效率。

因此，位置更新公式变更为式（7）所示：

3.3 MPSO-kmeans算法流程

本文采用粒子群算法融合k-means 算法进行改进优化，同时针对粒子群中存在的各参数相互独立、相互削弱影响力的问题加以改进，改进后的算法步骤如下：

步骤一：初始化，将学习因子c1s，c2s初始值，c1e，c2e终止值，wmax，wmin惯性权重最大、最小值，群体中粒子的速度、个体最优位置、群体最优位置等参数初始化，并将其随机分配到某一个类群中。

步骤二：运用粒子群算法搜寻最优的聚类中心。

1）采用式（3），调整粒子位置、速度，求出其适应度函数值；

2）比较当前粒子位置与历史最优位置的适应度函数值，如果当前位置适应度更优，那么使用此位置替换个体最好位置；

4）按照最近邻计算法则，把各粒子分类到对应的类簇；

5）利用新的类簇值计算出新的聚类中心，判断是否达到结束条件，如果达到，则结束，否则，迭代执行步骤1）。

步骤三：将新的中心输出到k-means，运行并得出结果。

4 实验分析

4.1 数据集获取与预处理

本文从微博获取文本数据，获取对象为某一位微博用户及其特别关注的100 名用户，获取的时间是2017 年9 月10 号到2017 年9 月30 号，对于每个用户取近20 天的相关数据，数据主要包括微博账号自身信息，发布博文，转发以及被转发的微博数［10］等。使用每个用户的这些数据，提取出其在当前时间段所感兴趣的两个话题。

对获取到的文本数据，进行预处理［11］，以便计算机对数据的处理分析，过程如下。

1）对获取到的文本数据进行清洗、分词、去停用词、提取特征词等操作；

2）将预处理后的数据使用向量空间模型进行表示，将其转变成计算机能处理的数据模型；

3）通过特征选择、权重计算，对模型再次处理；

4）对预处理数据，进行聚类分析。

以一位用户为例，预处理后的数据如表1 所示。

表1中，每一行中1表示此微博含有此特征词，如第二行数据表示第一条博文含有的特征词为“袁隆平”，“海水”，“水稻”，“改良”，“院士”，“盐碱地”，0表示无此特征词。

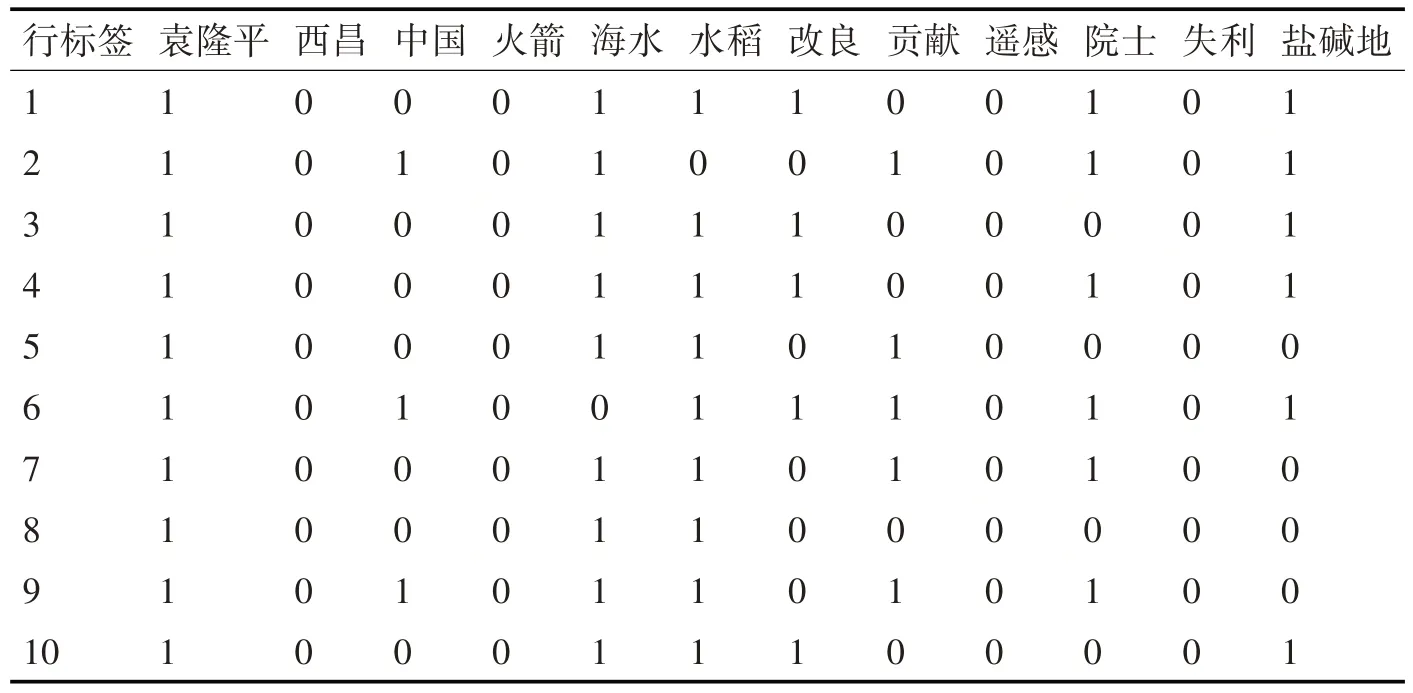
表1 各条博文的行特征词（部分）

4.2 实验分析

使用传统的k-means、传统粒子群和k-means混合算法、学习因子和飞行因子随惯性权重调整的MPSO-kmeans 算法进行实验。算法评价指标使用纯度值［12］，如式（8）所示：

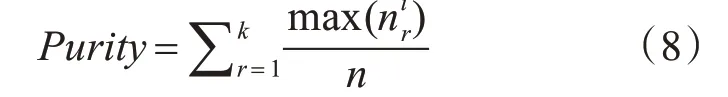
由于传统k-means 对初始聚类中心较为依赖，不同中心的选取在实验中产生的结果差别较大。因此使用传统k-means 运算5 次，取其平均值进行比较分析。实验得到的纯度如表2所示。

表2 聚类挖掘结果纯度比较

由表2纯度值可知：传统k-means的处理结果，虽然某些结果纯度值较高，但其5 次运算的平均值偏低，且波动较大。这是因为传统k-means 对初始中心的选择存在随机性的缘故。使用粒子群改进的k-means 算法可以很好地解决聚类结果波动较大的问题，使其不受初始聚类中心影响而产生较大波动。而结合了惯性权重、学习因子、飞行因子的MPSO-kmeans 算法，不仅提升了算法的全局搜索能力［13］，而且提升了算法的收敛精度［14］。实验表明 ，改 进 后 的MPSO-kmeans 同PSO-kmeans、k-means 相比，在挖掘结果上具有更好的挖掘纯度。

为了避免实验数据的局限性，随机选取的20名微博用户近20 天的博文，使用以上这三种算法对其文本信息进行聚类分析，实验结果如图1 所示。

图1 部分用户不同算法聚类纯度图

图1 中，横轴数字i 代表第i 位用户，纵轴表示聚类纯度值。 由图1 可知，使用k-means，PSO-kmeans，MPSO-kmeans 三种算法对微博用户在近20 天所感兴趣的两个话题进行了挖掘［15］。经过比较分析得出改进后的MPSO-kmeans 算法在聚类效果上存在较为明显的优势。

5 结语

本文对微博用户当前时间段感兴趣的话题进行研究，根据微博用户近20 天的博文信息，使用k-means 算法挖掘用户所感兴趣的话题。实验过程中，为了提高聚类效果，克服k-means 存在的缺陷，引入了粒子群优化算法，并对相关参数进行了优化，提升了全局搜索能力，能够更加精确、高效地完成聚类操作。实验表明，MPSO-kmeans 算法可很好地解决了受初始聚类中心影响大的问题，同时提高了算法的全局搜索能力以及局部寻优能力，具有更好的聚类效果。后续工作将根据聚类出的用户感兴趣话题，搜索相关话题的博文，建立推荐模型，给用户推荐其在当前时间段所感兴趣的博文，实现微博的个性化博文推送。