基于3σ准则的小波阈值法在去除红外图像噪声中的应用
2020-10-13孙婷婷崔少华
孙婷婷,崔少华
(1.淮北职业技术学院 计算机系,安徽 淮北 235000;2. 淮北师范大学 物理与电子信息学院,安徽 淮北 235000)
如今的社会安防中,监控作为最重要的一种手段被广泛应用于侦查、安全调查、事故分析等领域。安防监控主要包含可见光拍摄和红外拍摄,其中,可见光拍摄系统具有高分辨率、细腻的纹理信息等优点,能充分显示物体细节,多应用于事故分析与工业故障检测领域。相比可见光图像,红外拍摄对天气、环境等因素要求低,夜晚也能正常拍摄,因而在社会中应用更加宽泛,主要应用于社会安防领域。然而,采集的红外图像由于受到噪声的干扰使得图像质量下降,严重影响后续的识别和目标跟踪。因此对红外图像去噪,提高图像信噪比,具有重要的实际意义。传统的红外图像去噪主要采用滤波法,通过不同模板滤波器将图像信息和噪声分离,从而舍去噪声部分,然而滤波法忽略了图像的细节信息和边缘部分,使得去噪后的图像模糊失真。之后,小波分解法由于有效的处理效果被广泛应用于红外图像,例如,代少升等[1]采用多级小波分解与重构实现图像去噪,并与传统中值滤波进行比较,验证了小波分析法的可行性与有效性。为了更有效的去除噪声,翟进有等[2]采用小波阈值法处理红外图像,改进了传统半软阈值法在阈值附近图像不平滑的缺点。为了进一步改善小波阈值去除红外图像所含噪声的效果,本文以“3σ”准则为基础,探讨小波分析法中阈值选取的重要性,并给出阈值选取的方法,来源于俄亥俄州立大学提供的OSU Color-Thermal Database数据库中红外图像去噪实验表明,本文方法能有效去除噪声,相比传统小波阈值法,能更好地提高信噪比和处理细节。
1 小波分解与重构法
小波变换的实质是对小波函数进行伸缩平移,借助小波函数分解信号得到一系列小波系数。设小波函数ψ(t)∈L2(R),图像信号f(u)∈L2(R),则连续小波变换公式为[3]:

(1)



(2)
上式成立的条件为,ψ在0 (3) 小波变换是将有用信号的能量集中在小波域中少数的小波系数上,而高斯白噪声在任何一层小波分解域中依然是白噪声,因此噪声的能量是分散于整个小波域上的。小波分解后,图像信号的小波系数幅度大于噪声小波系数幅度,这不失一般性。重构时选取多少个图像小波系数是去噪的关键,若选取的个数过多则会引入过多的噪声,去噪效果欠佳,反之会舍弃过多图像信息,去噪后丢失大量细节。因此,实际去噪时,通常设置一个合适的门限(阈值)处理含噪图像的小波系数,以避免上述关键问题。软硬阈值去噪法正是基于这种原理[6]。将分解后的小波系数进行阈值处理包含硬阈值和软阈值2种方法,数学公式如下所示。硬、软阈值均认为大于阈值的系数对应图像信息,小于阈值的系数对应噪声并将其置零。 (4) 软阈值法:x=T(y,t)= (5) 上式中:x是处理后小波系数,T是阈值函数,y是分解后小波系数,t是阈值。阈值计算为: (6) 式(6)中,N是图像的大小。 然而,红外图像作为典型的多维信号容易受到高斯噪声的影响,传统硬软阈值法在确定关键的阈值时,弱化了高斯噪声的统计特性。由于高斯白噪声在各个尺度分解所得的小波系数仍然是高斯的,阈值的选取不应该简单的以函数形式确定,应该以数理统计为基础。“3σ”去噪法正是在这种背景下提出的,具体描述为:若图像中各噪声点wN(x)~N(μ,σ2),由概率论统计知识可得[7]: P{-3σ≤wN(x)-μ≤3σ}=0.997 4 (7) 由上式可知,噪声点幅值的绝对值落在3σ的范围高达99%,几乎包含了所有的噪声点。因此选定3σ为小波重构的阈值,即:含噪图像分解后的小波系数中,若绝对值大于3σ则保留(认为是图像信息),若绝对值小于3σ则将小波系数置零(认为是噪声的)。采用保留的小波系数进行重构就可得去噪后的红外图像。 实验图像来源于俄亥俄州立大学提供的OSU Color-Thermal Database红外数据库[8],由200幅图像组成,每幅图像含有人体目标和背景目标,具有广泛的应用性。随机选取其中1幅红外图像,加入15%的高斯随机噪声,分别采用小波硬、软阈值去噪法、本文所述3σ去噪法、奇异值分解算法(singular value decomposition,SVD)进行去噪实验,结果如图1所示。 由图2 可知,相比其他算法,本文所述的去噪法在还原红外图像的细节和边缘部分效果最好。其中,硬、软阈值法去噪后均存在轮廓不清楚,边界模糊,细节损失严重的问题。根据公式(5)可知,软阈值法在保留下来的小波系数中进一步去除高斯噪声,因此相比硬阈值,图2中软阈值去噪后包含的噪声点更少,但是舍弃的小波系数更多,从而导致红外图像还原效果更差。观察图2 可知,SVD去噪后包含的噪声点相对较少,这是由于借助于奇异值分解图,SVD能轻易的找到拐点(图像和噪声的分界点),重构时只需选取拐点之前的奇异值即可[9]。因此SVD去除的噪声更多,然而付出的代价就是损失较多图像的细节。为了定量对比不同算法的去噪效果,本文采用图像去噪中普遍采用的峰值信噪比(Peak signal to noise ratio,PSNR)进行衡量,结果如表1所示。其中PSNR定义[10-11]为: (8) 式中,y是原始红外图像数据,yo是去除噪声后图像数据,N是图像维数,‖·‖是L2范数。PSNR值越大表明红外图像重构的效果越好。表1可知,本文所述3σ去噪法的PSNR最大,表明基于高斯统计分布的阈值确定法还原图像的效果最好。 表1 不同算法去噪后PSNR值 在红外图像去噪领域中,基于3σ的小波分解算法能有效去除图像中所含的高斯噪声,该算法以高斯随机噪声的统计特性出发确定小波重构阈值,去噪后图像对原始图像的还原效果更好。然而,无论是小波分解算法还是SVD算法,均是采用在图像信息中舍弃噪声达到去噪目的,去噪后都存在图像细节的损失现象,这是该类算法的弊端。在接下来的工作中,将探索改进的算法去除红外图像噪声,以便保留更多的图像信息。

2 传统小波阈值法


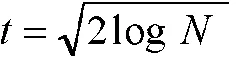
3 3σ去噪
4 实验结果

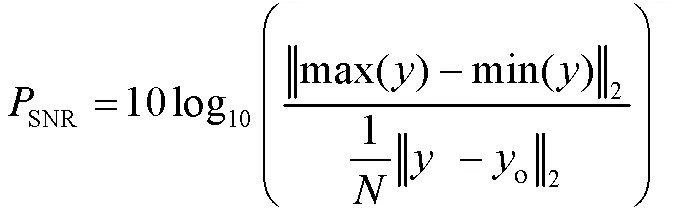

5 结论
